Планы экспериментов из восьми опытов
12.4. Планы экспериментов из восьми опытов
Для рассмотренных в этой главе факторных планов экспериментов из восьми опытов важно понять, что все двухуровневые регулярные неполные факторные планы из восьми опытов с числом факторов до семи могут быть созданы на основе, показанной в таблице 12.4.1 матрицы уровней с ортогональными столбцами. Эта матрица получается записью в стандартном порядке столбцов уровней трёх нормированных факторов х1, х2 и х3, а также полученных на их основе с использованием произведения Адамара столбцов уровней взаимодействий между этими факторами. В таблице 12.4.2 показано как эта матрица с ортогональными столбцами используется для создания планов 2IV4–1 и 2III7–4.
Присваивая факторам х1, х2, ..., х7 уровни соответственно семи столбцов х1, х2, …, х123, получаем насыщенный план 2III7–4. В нём матрица уровней из таблицы 12.4.1 используется для максимального числа факторов. Любой другой дробный план из восьми опытов может быть получен исключением некоторых столбцов из этого семифакторного основного плана. Например, если не использовать столбцы х12, х13 и х23 уровней взаимодействий исходных факторов для уровней новых факторов х4, х5 и х6, то получается план 2IV4–1 для факторов х1, х2, х3 и х4. Планы 2III5–2 и 2III6–3 для изучения соответственно пяти и шести факторов в эксперименте из восьми опытов могут быть получены использованием одного или двух столбцов х12, х13 и х23 уровней двухфакторных взаимодействий для уровней новых факторов х5 и х6.
Таблица 12.4.1. Матрица уровней для создания дробных планов из восьми опытов
| х1 | х2 | х3 | х12 | х13 | Рекомендуемые материалыFREE Бараненков Г. С., Демидович Б. П., Ефименко В. А. - Задачи и упражнения по математическому анализу для втузов - 2004 На двух автоматах изготавливаются одинаковые детали. Производительность первого автомата в 2 раза больше, чем второго. Вероятность изготовления детали высшего качества на первом автомате — 0,95, а на втором — 0,97. Детали с обоих автоматов поступают Номотех. Pdf-файл с поиском по всей теории из номотеха. FREE Часть 3. Математический анализ - кратные и криволинейные интегралы. FREE Краснов М.Л., Киселев А.И. , Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Задачи и упражнения (2-е изд., 1981) Уравнения математической физики (Кузнецов Л.А.) х23 | х123 |
| –1 | –1 | –1 | +1 | +1 | +1 | –1 |
| +1 | –1 | –1 | –1 | –1 | +1 | +1 |
| –1 | +1 | –1 | –1 | +1 | –1 | +1 |
| +1 | +1 | –1 | +1 | –1 | –1 | –1 |
| –1 | –1 | +1 | +1 | –1 | –1 | +1 |
| +1 | –1 | +1 | –1 | +1 | –1 | –1 |
| –1 | +1 | +1 | –1 | –1 | +1 | –1 |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Таблица 12.4.2. Ортогональные векторы уровней и соответствующие им факторы в узловых планах экспериментов из восьми опытов
| Планы | х1 | х2 | х3 | х12 | х13 | х23 | х123 | Проективность Р |
| 23 | х1 | х2 | х3 | |||||
| 2IV4–1 | х1 | х2 | х3 | х4 | 3 | |||
| 2III7–4 | х1 | х2 | х3 | х4 | х5 | х6 | х7 | 2 |
Четырёхфакторный план 2IV4–1 и семифакторный план 2III7–4 называются узловыми планами, так как при восьми опытах и данной разрешающей способности они включают наибольшее число факторов. Структуры совместных воздействий для семифакторного узлового плана эксперимента показаны в таблице 12.3.3, а структуры совместных воздействий для четырёхфакторного узлового плана эксперимента получаются на основе таблицы 12.2.2.
Последовательное экспериментирование
Среди статистических методов экспериментальных исследований описываемый в книгах метод постановки одного эксперимента подходит в ситуации, где окончательные решения должны делаться на основе данных только этого эксперимента, который не может быть продолжен. В социальных науках существует много таких ситуаций, и такой эксперимент является единственно возможным. Но это нетак для промышленных и инженерных исследований. Цель нашего изложения показать большую ценность планируемого экспериментирования в качестве средства ускорения последовательного процесса научного познания.
Необходимо помнить, что при планируемом экспериментировании, как и при любом исследовании, делается ряд предположений, которые сильно влияют на его выполнение. Необходимость этих предположений никак не связана с использованием статистического плана эксперимента. Они должны делаться при любом методе экспериментирования. В начале эти предположения содержат следующее: какие факторы включать в исследование, какие отклики измерять, где расположить область эксперимента, как изменять факторы, а когда данные получены, то, как продолжить. При постановке одного эксперимента все эти предположения рассматриваются как предварительно заданные.
Однако, очевидно, что разные экспериментаторы сделают разные предположения. Поэтому целью любой методологии последовательного экспериментирования не может быть уникальность, а скорее стратегия, которая вероятно приведёт к полезному решению. Структурное экспериментирование может дать экспериментатору наиболее ясную информацию о воздействиях факторов и их взаимодействий на каждый из разных откликов. Возможность сделать второе предположение предоставляет наилучший шанс понять, что происходит. Специалист предметной области исследования может строить на этом своё понимание. Ничто не может устранить неопределённость, но профессиональное интерактивное использование соответствующих методов может чрезвычайно уменьшить её влияние.
В этой связи нет необходимости отвечать на все вопросы постановкой одного эксперимента. Меньшие эксперименты, которые последовательно сокращают число неопределённостей и ведут к большей ясности, являются намного более эффективными. Таким же образом малое число тщательно выбранных опытов не обязательно ведут к однозначному объяснению. Когда они сами ещё не дают данные для решения проблемы, то они могут служить для устранения большого числа неопределённостей и дают основу для дальнейших предположений.
Оценка отделённых воздействий факторов
Когда результаты выполняемых по неполным планам экспериментов дают неясности, то могут понадобиться дополнительные опыты. Для этого одним из используемых методов в последовательном экспериментировании является метод планирования дополнительных опытов путём изменения знаков уровней на противоположные в столбцах матрицы имеющегося неполного плана. Описание и примеры использования этого метода путём изменения знаков на противоположные для уровней факторов и оценки воздействий факторов, отделённых от воздействий двухфакторных взаимодействий, приводятся в [Box с соавт. (2005) стр.249; Box, Draper (2007) стр.142]. Процедура оценки воздействия одного фактора или воздействий группы факторов, отделённых от воздействий факторных взаимодействий, может использоваться для любой части или всего исходного дробного плана.
В эксперименте с пневматическим преобразователем линейных перемещений из раздела 12.3 важно было выявить активные факторы. Для этого использовался представленный в таблице 12.3.2 узловой план 2III7–4 эксперимента из восьми опытов. Опыты проводились в случайной последовательности, и было замечено, что в опытах 2 и 6 получалось наименьшее усреднённое время срабатывания. В этих опытах активные факторы х1 эффективной площади мембраны и х2 проходного сечения дросселя сопло-заслонка устанавливались соответственно на верхнем и нижнем уровнях. Поэтому было возможно, что допустимые увеличение эффективной площади мембраны и уменьшение проходного сечения дросселя сопло-заслонка ведут к уменьшению времени срабатывания. Однако другие активные факторы х3 проходного сечения входного дросселя камеры противодавления и х7 давления сжатого воздуха на входе в преобразователь в опыте 6 устанавливались соответственно на верхнем и нижнем уровнях, а в опыте 2 на нижнем и верхнем уровнях. Поэтому влияние этих факторов на время срабатывания было неясным и для лучшего понимания того, что происходит, были необходимы дополнительные опыты.
В таблице 12.3.3 показаны структуры совместных воздействий и результаты их оценки. Четыре значения b1, b2, b3 и b7 являются большими. Но структуры совместных воздействий показывают, что воздействие фактора х3 совмещено с воздействиями β15, β26, β47 от взаимодействий активных факторов х1, х2 и х7 с неактивными факторами х4, х5 и х6, а воздействие фактора х7 совмещено с воздействиями β16, β25, β34 от взаимодействий активных с неактивными факторами. Может некоторые воздействия от взаимодействий активных факторов с неактивными здесь являются большими?
Из-за указанных неопределённостей в случае эксперимента по неполному плану разрешающей способности III рекомендуется ставить дополнительные опыты [Box, Draper (2007) стр.140]. Поэтому было решено выполнить восемь дополнительных опытов по плану, получаемому посредством изменения на противоположные всех знаков уровней семи столбцов матрицы исходного плана в таблице 12.3.2. Таким образом, знаки элементов семи столбцов вновь созданной матрицы плана были изменены на обратные тем, которые в матрице исходного плана. В таблице 12.4.3 показан полученный таким образом план вместе с новыми данными, проведённого по этому плану эксперимента.
Таблица 12.4.3. Дополнительный план из восьми опытов и их результаты для изучения влияний семи факторов и их парных взаимодействий
| Опыты | х1 | х2 | х3 | х4 | х5 | х6 | х7 | у1 | у2 | у3 |
|
| –х1 | –х2 | –х3 | –х4 | –х5 | –х6 | –х7 | |||||
| 9 | +1 | +1 | +1 | –1 | –1 | –1 | +1 | 89 | 100 | 95 | 95 |
| 10 | –1 | +1 | +1 | +1 | +1 | –1 | –1 | 154 | 146 | 152 | 151 |
| 11 | +1 | –1 | +1 | +1 | –1 | +1 | –1 | 85 | 90 | 88 | 88 |
| 12 | –1 | –1 | +1 | –1 | +1 | +1 | +1 | 103 | 98 | 97 | 99 |
| 13 | +1 | +1 | –1 | –1 | +1 | +1 | –1 | 123 | 121 | 122 | 122 |
| 14 | –1 | +1 | –1 | +1 | –1 | +1 | +1 | 148 | 150 | 151 | 150 |
| 15 | +1 | –1 | –1 | +1 | +1 | –1 | +1 | 96 | 107 | 101 | 101 |
| 16 | –1 | –1 | –1 | –1 | –1 | –1 | –1 | 130 | 134 | 133 | 132 |
Полным определяющим отношением для узлового плана 2III7–4 является 1=х1◦х2◦х4 =х1◦х3◦х5=х2◦х3◦х6=х1◦х2◦х3◦х7=х2◦х3◦х4◦х5 =х1◦х3◦х4◦х6 =х3◦х4◦х7 =х1◦х2◦х5◦х6 =х2◦х5◦х7 =х1◦х6◦х7=х4◦х5◦х6 =х1◦х4◦х5◦х7 =х2◦х4◦х6◦х7=х3◦х5◦х6◦х7 =х1◦х2◦х3◦х4◦х5◦х6◦х7. Полное определяющее отношение для дополнительного узлового плана 2III7–4 отличается знаками минус у членов с нечётным числом сомножителей, то есть, имеем 1=–х1◦х2◦х4=–х1◦х3◦х5 =–х2◦х3◦х6=х1◦х2◦х3◦х7=х2◦х3◦х4◦х5 =х1◦х3◦х4◦х6 =–х3◦х4◦х7 =х1◦х2◦х5◦х6=–х2◦х5◦х7 =–х1◦х6◦х7 =–х4◦х5◦х6 =х1◦х4◦х5◦х7=х2◦х4◦х6◦х7=х3◦х5◦х6◦х7 =–х1◦х2◦х3◦х4◦х5◦х6◦х7. Если это определяющее отношение умножить на х1 и считать, что все трёхфакторные и более высокого порядка взаимодействия дают пренебрежимо малые воздействия, то соответствующие им члены определяющего отношения можно сократить и на основе оставшихся х1=–х2◦х4=–х3◦х5=–х6◦х7 получается сокращенная структура β1–β24–β35–β67 совместных воздействий фактора х1 и двухфакторных взаимодействий. Сокращённые структуры совместных воздействий всех остальных факторов и двухфакторных взаимодействий приведены в таблице 12.4.4.
Оценка совместных воздействий факторов и двухфакторных взаимодействий делается методом наименьших квадратов с использованием постулируемой модели у=β0'+β1'х1+β2'х2+β3'х3+β4'х4+β5'х5+β6'х6+β7'х7+ε и вектора  усреднённых значений переменных отклика из таблицы 12.4.4. Найденные результаты оценки представлены в таблице 12.4.4.
усреднённых значений переменных отклика из таблицы 12.4.4. Найденные результаты оценки представлены в таблице 12.4.4.
Как и для исходного плана, для дополнительного плана структуры совместных воздействий факторов и их двухфакторных взаимодействий можно установить на основе матрицы совмещения воздействий. Эта матрица для дополнительного плана показана в таблице 12.4.5. В ней все коэффициенты с отрицательными знаками.
С целью отделения воздействий факторов от воздействий их двухфакторных взаимодействий находят усреднённые структур совместных воздействий полученных для начального и дополнительного экспериментов. Затем то же делается с результатами оценки структур совместных воздействий начального и дополнительного экспериментов. В таблице 12.4.6 показано, что при таких усреднениях воздействия двухфакторных взаимодействий сокращаются и получаются только воздействия факторов. Кроме этого, если найти половины разностей структур совместных воздействий и результатов их оценки для указанных экспериментов, то получаются структуры только совместных воздействий двухфакторных взаимодействий и результаты их оценки, что также показано в таблице 12.4.6.
Таблица 12.4.4. Структуры совместных воздействий факторов и двухфакторных взаимодействий и результаты их оценки по данным дополнительного эксперимента по плану 2III7–4
| Факторы | Совместные воздействия | Результаты оценки |
| 1. Эффективная площадь мембраны, х1 | β1–β24–β35–β67 | b1'=–15,792 |
| 2. Проходное сечение дросселя сопло-заслонка, х2 | β2–β14–β36–β57 | b2'=12,042 |
| 3. Проходное сечение входного дросселя, х3 | β3–β15–β26–β47 | b3'=–9,125 |
| 4. Объём рабочей камеры, х4 | β4–β12–β37–β56 | b4'=5,125 |
| 5. Жёсткость пружины, х5 | β5–β13–β27–β46 | b5'=1,125 |
| 6. Объём камеры противодавления, х6 | β6–β17–β23–β45 | b6'=–2,542 |
| 7. Давление на входе в преобразователь, х7 | β7–β16–β25–β34 | b7'=–5,958 |
| Среднее переменных отклика в опытах эксперимента | b0'=117,208 |
Таблица 12.4.5. Матрица коэффициентов совмещения воздействий для дополнительного эксперимента по плану 2III7–4
| β12 | β13 | β14 | β15 | β16 | β17 | β23 | β24 | β25 | β26 | β27 | β34 | β35 | β36 | β37 | β45 | β46 | β47 | β56 | β57 | β67 | |
| β0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| β1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | –1 |
| β2 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | –1 | 0 |
| β3 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 |
| β4 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | –1 | 0 | 0 |
| β5 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 |
| β6 | 0 | 0 | 0 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 |
| β7 | 0 | 0 | 0 | 0 | –1 | 0 | 0 | 0 | –1 | 0 | 0 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 12.4.6. Оценка воздействий по результатам двух экспериментов
| Факторы | Вычисление воздействий | Результаты оценки |
| х1 | (β1+β24+β35+β67+β1–β24–β35–β67)/2=β1 | (b1+b1')/2=–14,521 |
| х2 | (β2+β14+β36+β57+β2–β14–β36–β57)/2=β2 | (b2+b2')/2=13,313 |
| х3 | (β3+β15+β26+β47+β3–β15–β26–β47)/2=β3 | (b3+b3')/2=–9,479 |
| х4 | (β4+β12+β37+β56+β4–β12–β37–β56)/2=β4 | (b4+b4')/2=4,021 |
| х5 | (β5+β13+β27+β46+β5–β13–β27–β46)/2=β5 | (b5+b5')/2=2,062 |
| х6 | (β6+β17+β23+β45+β6–β17–β23–β45)/2=β6 | (b6+b6')/2=–0,604 |
| х7 | (β7+β16+β25+β34+β7–β16–β25–β34)/2=β7 | (b7+b7')/2=–7,146 |
| х24+х35+х67 | (β1+β24+β35+β67–β1+β24+β35+β67)/2=β24+β35+β67 | (b1–b1')/2=1,271 |
| х14+х36+х57 | (β2+β14+β36+β57–β2+β14+β36+β57)/2=β14+β36+β57 | (b2–b2')/2=1,271 |
| х15+х26+х47 | (β3+β15+β26+β47–β3+β15+β26+β47)/2=β15+β26+β47 | (b3–b3')/2=–0,354 |
| х12+х37+х56 | (β4+β12+β37+β56–β4+β12+β37+β56)/2=β12+β37+β56 | (b4–b4')/2=–1,104 |
| х13+х27+х46 | (β5+β13+β27+β46–β5+β13+β27+β46)/2=β13+β27+β46 | (b5–b5')/2=0,937 |
| х17+х23+х45 | (β6+β17+β23+β45–β6+β17+β23+β45)/2=β17+β23+β45 | (b6–b6')/2=1,937 |
| х16+х25+х34 | (β7+β16+β25+β34–β7+β16+β25+β34)/2=β16+β25+β34 | (b7–b7')/2=–1,187 |
| блоков х8 | (b0–b0')/2=0,688 | |
| Среднее | (b0+b0')/2=117,896 |
Объединение двух экспериментов и анализ результатов
Совокупность опытов начального и дополнительного экспериментов можно считать объединённым экспериментом и в нём все опыты повторялись трижды. Два эксперимента можно рассматривать как два блока по 8 опытов и оценить воздействие фактора х8 блоков, как показано в таблице 12.4.6.
Матрицу плана объединённого эксперимента можно представить в виде Х2= , где Х1 – матрица плана начального эксперимента. Модель эксперимента по такому плану имеет вид
, где Х1 – матрица плана начального эксперимента. Модель эксперимента по такому плану имеет вид
у=β0+β1х1+β2х2+β3х3+β4х4+β5х5+β6х6+β7х7+β24х24+β14х14+β15х15
+β12х12+β13х13+β23х23+β34х34+β8х8+ε, (12.4.1)
где фактор х24 имеет вектор уровней такой же, как факторы х35 и х67. Поэтому он представляет структуру х24+х35+х67 совместных двухфакторных воздействий. Фактор х14 по той же причине представляет структуру х14+х36+х57, фактор х15 – структуру х15+х26+х47, фактор х12 – структуру х12+х56+х37, фактор х13 - структуру х13+х46+х27, фактор х23 – структуру х23+х45+х17, фактор х34 – структуру х34+х25+х16 и х8 - фактор блоков.
Матрица модели этого эксперимента имеет вид Х=[1 X2 х24 х14 х15 х12 х13 х23 х34 x8], где x8 - вектор уровней фактора блоков, в котором первые восемь элементов равны +1, а остальные восемь равны –1. Векторы х24, х14, х15, х12, х13, х23 и х34 являются векторами уровней первых двухфакторных взаимодействий структур совместных двухфакторных воздействий. Вектор усреднённых значений переменных отклика в этом эксперименте  =
= , где векторы
, где векторы  и
и  взяты из таблиц 12.3.2 и 12.4.4. Вектор оценки параметров этой модели вычисляется методом наименьших квадратов по формуле
взяты из таблиц 12.3.2 и 12.4.4. Вектор оценки параметров этой модели вычисляется методом наименьших квадратов по формуле  =(ХТХ)–1ХТ
=(ХТХ)–1ХТ и
и
 Т=[117,896 –14,521 13,312 –9,479 4,021 2,062 –0,604 –7,146 1,271
Т=[117,896 –14,521 13,312 –9,479 4,021 2,062 –0,604 –7,146 1,271
1,271 –0,354 –1,104 0,937 1,937 –1,187 0,688]. (12.4.2)
Элементы этого вектора совпадают с полученными в таблице 12.4.7 результатами оценки воздействий факторов и структур совместных двухфакторных взаимодействий.
Рекомендация для Вас - Деятельность государства по созданию благоприятных экономических условий для сельскохозяйственных производителей.
Фактор блоков является восьмым фактором объединённого эксперимента. Поэтому этот эксперимент имеет план 2IV8–4 с матрицей [X2 x8]. Для данного эксперимента, также как и для начального, можно найти стандартную ошибку результатов оценки воздействий на отклик. Она получена равной ±0,949. Сравнение найденных результатов оценки воздействий с их стандартной ошибкой показывает, что представленные в таблице 12.4.6 жирным шрифтом пять результатов оценки воздействий факторов х1, х2, х3, х4 и х7 явно выделяются из шума. В итоге получается, что активными являются пять факторов.
Для выявления реальных воздействий можно использовать и графический метод. Для найденных результатов оценки воздействий можно построить график кумулятивных вероятностей их распределения, как и для найденных с использованием полного факторного плана результатов оценки в разделе 11.3. Для результатов оценки из таблицы 12.4.6 такой график показан на Рис.12.4.1. На графике видно, что пять воздействий факторов х1, х2, х3, х4 и х7 выделяются из шума создаваемого воздействиями факторов х8, х5 и х6, а также структурами совместных двухфакторных взаимодействий.
Применение рассмотренного метода отделения воздействий факторов с воздействий двухфакторных взаимодействий в данном случае привело к появлению ещё одного активного фактора х4 - объём рабочей камеры. Этот метод также показывает, как неполные факторные планы используются в последовательном экспериментировании. Начальный эксперимент по неполному факторному плану дал возможность отсеять некоторое число факторов, но неясности оставались. Результаты второго эксперимента по изменённому плану вместе с результатами первого дали возможность отделить воздействия факторов от воздействий двухфакторных взаимодействий и увеличить точность результатов оценки.
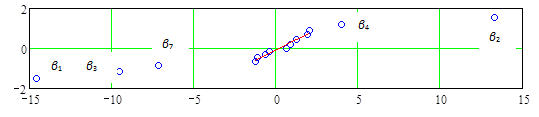
Рис.12.4.1. График кумулятивных вероятностей результатов оценки воздействий на основе данных эксперимента по плану 28-4.
Выявление фактора х4 активным было существенным для объяснения зависимости быстродействия преобразователя от объёма рабочей камеры. В общем, на основе результатов начального и дополнительного экспериментов получена возможность объяснить влияние включённых в эксперимент факторов на время срабатывания пневматического преобразователя, и эти знания представляли большую ценность для улучшения его быстродействия, как для исходной схемы, так и для новых.



 переменных отклика
переменных отклика 


















