Обобщенный метод получения математических моделей систем
Обобщенный метод получения математических моделей систем
Математической моделью технического объекта на макроуровне является система обыкновенных дифференциальных уравнений, в общем случае не разрешенная относительно производных, т. е.  , где v - вектор фазовых переменных; t - время, независимая переменная; F - вектор-функция;
, где v - вектор фазовых переменных; t - время, независимая переменная; F - вектор-функция;  . Подобную систему уравнений в общем случае можно решить только с помощью численных методов интегрирования, поскольку эта система высокого порядка и нелинейна. Результат решения ММ системы (ММС) - зависимости фазовых переменных от времени.
. Подобную систему уравнений в общем случае можно решить только с помощью численных методов интегрирования, поскольку эта система высокого порядка и нелинейна. Результат решения ММ системы (ММС) - зависимости фазовых переменных от времени.
Обобщенная ММС может быть представлена в виде системы уравнений:
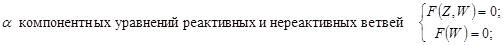
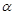
 (3)
(3)
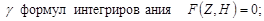
где Н - вектор переменных состояния, т. е. фазовых переменных, непосредственно характеризующих запасы энергии в системе (переменных типа разности потенциалов на ветвях типа С и переменных типа потока через ветви типа L); W - вектор остальных фазовых переменных; Z - вектор производных переменных состояния по времени.
Эти уравнения составлены при условии, что эквивалентная схема содержит  элементов из которых
элементов из которых  реактивных. Реактивными считаются элементы, способные накапливать энергию, т.е. типа С и L (емкости, индуктивности, массы, упругости ...).
реактивных. Реактивными считаются элементы, способные накапливать энергию, т.е. типа С и L (емкости, индуктивности, массы, упругости ...).
Количество неизвестных в этих уравнениях  , так как размерности векторов Н и Z равны
, так как размерности векторов Н и Z равны  , а вектора
, а вектора  . Таким образом, система уравнений (3) - замкнутая.
. Таким образом, система уравнений (3) - замкнутая.
Рекомендуемые материалы
Совокупность неизвестных переменных в уравнениях, описывающих поведение технической системы, называется вектором базисных координат или базисом метода.
Базис обобщенного метода составляют переменные типа разности потенциалов для всех элементов, переменные типа потока для всех ветвей и переменные типа производных переменных состояния.
В матричном виде ММС обобщенного метода можно записать следующим образом:
 (4)
(4)
где 1 - единичная подматрица; D3 и D4 - диагональные подматрицы, содержащие на диагонали 1 или 0.
Для подматрицы D3 компонентное уравнение  даст на диагонали 1, а компонентное уравнение
даст на диагонали 1, а компонентное уравнение  даст по диагонали 0, поскольку в нем отсутствует
даст по диагонали 0, поскольку в нем отсутствует  . Подматрица К31 связывает между собой
. Подматрица К31 связывает между собой  и Ux, т. е. ее элементы суть коэффициенты перед Ux в компонентных уравнениях хорд. Подматрица К42 связывает между собой Iв.д и Uв.д, т. е. ее элементы суть коэффициенты перед Iв.д в компонентных уравнениях ветвей дерева. Подвекторы
и Ux, т. е. ее элементы суть коэффициенты перед Ux в компонентных уравнениях хорд. Подматрица К42 связывает между собой Iв.д и Uв.д, т. е. ее элементы суть коэффициенты перед Iв.д в компонентных уравнениях ветвей дерева. Подвекторы  и
и  - постоянные члены в компонентных уравнениях. Подматрицы К32, К34, K41, К43 - нулевые только при наличии зависимых ветвей, например элемент с уравнением
- постоянные члены в компонентных уравнениях. Подматрицы К32, К34, K41, К43 - нулевые только при наличии зависимых ветвей, например элемент с уравнением  даст ненулевой элемент в подматрицу К34. Элементы подматриц К35 и К45 суть коэффициенты в компонентных уравнениях реактивных элементов перед Z. Подматрицы К51, …, К54 связывают между собой переменные состояния, которые могут принадлежать как ветвям дерева, так и хордам, с их производными (подвектор Z) через формулы интегрирования, в общем виде имеющие вид:
даст ненулевой элемент в подматрицу К34. Элементы подматриц К35 и К45 суть коэффициенты в компонентных уравнениях реактивных элементов перед Z. Подматрицы К51, …, К54 связывают между собой переменные состояния, которые могут принадлежать как ветвям дерева, так и хордам, с их производными (подвектор Z) через формулы интегрирования, в общем виде имеющие вид:  , тогда коэффициент
, тогда коэффициент  будет элементом подматриц К51, ..., К54, а коэффициент
будет элементом подматриц К51, ..., К54, а коэффициент  будет элементом подвектора
будет элементом подвектора  .
.
Решение подобной системы уравнений возможно итерационными методами, наиболее распространенным из которых является метод Ньютона. Алгоритм метода Ньютона предусматривает многократное решение линеаризованной системы уравнений:  , где
, где  матрица Якоби;
матрица Якоби;  - вектор поправок к неизвестным X;
- вектор поправок к неизвестным X;  - вектор невязок.
- вектор невязок.
Пример получения математической модели гидромеханической системы (обобщенным методом).
Эквивалентная схема гидромеханической системы представлена на рис. 3, а.
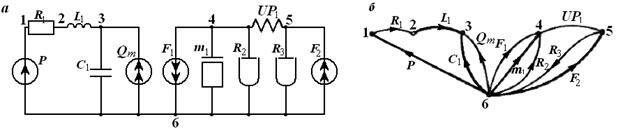
Рис. 3. Эквивалентная схема гидромеханической системы (а) и ее граф (б) с выделенным фундаментальным деревом.
Граф эквивалентной схемы изображен на рис. 3, б. Направления переменных типа потока в ветвях задаем произвольно (кроме источников потока). Если заданное и истинное направления не совпадают, то получим значения переменных типа потока со знаком минус. Дерево графа выделено жирными линиями. В обобщенном методе дерево выбирается произвольным, т.е. не обязательно нормальным.
Используя уравнения (1) и (2), получим топологические уравнения системы. М-матрица представлена в таблице 3. Нулевые элементы в ней не проставлены.
Таблица 3
| Р | L | C | M | F2 | |
| R1 | +1 | +1 | -1 | ||
| Qm | -1 | ||||
| F1 | -1 | ||||
| R2 | -1 | ||||
| UP | +1 | -1 | |||
| R3 | +1 |
Система топологических уравнений такова:

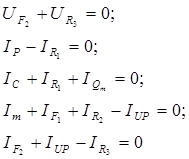
Вектор неизвестных для этого примера будет содержать следующие элементы:
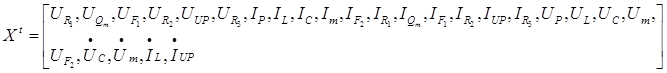
Расположение переменных в этом векторе следующее: подвектор Ux, подвектор IВ.Д, подвектор Ix, подвектор UВ.Д, подвектор производных переменных состояния для реактивных элементов. Система уравнений типа  представлена так, как показано на следующем рисунке.
представлена так, как показано на следующем рисунке.
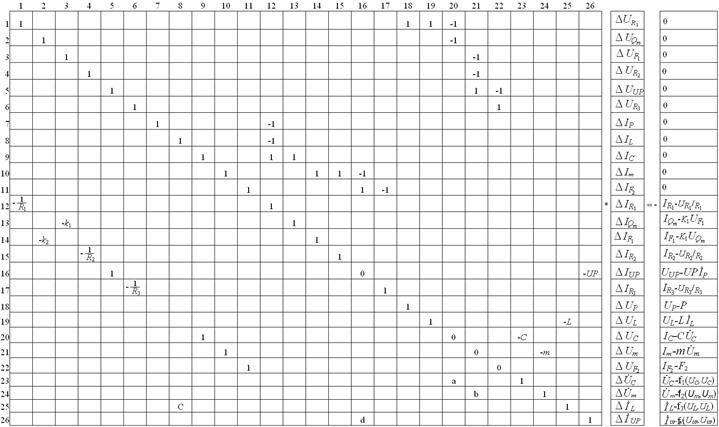
Вектор невязок составлен из следующих подвекторов: нулевой подвектор (уравнения 1, ..., 11); подвектор, получаемый из компонентных уравнений 12,...., 22; подвектор, получаемый из формул интегрирования (уравнения 23, ..., 26); f1, ..., f4 - формулы интегрирования соответствующего дифференциального уравнения, причем не обязательно одинаковые, для каждого реактивного элемента может быть использована своя формула интегрирования:  ,
,  ,
,  ,
,  - векторы значений соответствующих переменных состояния на предыдущих шагах интегрирования, поскольку формула интегрирования выглядит следующим образом:
- векторы значений соответствующих переменных состояния на предыдущих шагах интегрирования, поскольку формула интегрирования выглядит следующим образом:
Информация в лекции "Кэш-память" поможет Вам.
 (5)
(5)
где  зависит от порядка метода интегрирования и шага интегрирования
зависит от порядка метода интегрирования и шага интегрирования  , а
, а  зависит, кроме того, от вектора значений переменных состояния на одном или нескольких предыдущих шагах.
зависит, кроме того, от вектора значений переменных состояния на одном или нескольких предыдущих шагах.
Коэффициенты а, в, с, d в матрице Якоби суть коэффициенты, получаемые после дифференцирования формулы (3) по соответствующей переменной. Если используется один метод интегрирования для всех дифференциальных уравнений, то коэффициенты равны между собой.
Для неявного метода первого порядка - метода Эйлера, формула которого  , коэффициенты равны 1/h.
, коэффициенты равны 1/h.
Для метода Гира второго порядка, формула которого  , коэффициенты равны
, коэффициенты равны  .
.
Рассмотрим, как необходимо представить модели некоторых элементов при их включении в библиотеку комплекса анализа динамических систем, если в этом комплексе реализован обобщенный алгоритм формирования ММС.





















