Алгоритмы формирования случайной выборки
9. Алгоритмы формирования случайной выборки
9.1. Последовательное извлечение
Утверждение.
Следующая процедура отбора приводит к простой случайной выборке без возвращения:
· Извлечь первый элемент из совокупности N элементов с вероятностью равной 1/N;
· Извлечь второй элемент из оставшихся 
элементов с вероятностью равной 1/(
).
...
· Извлечь n-ый элемент из оставшихся 
элементов с вероятностью 
.
Комментарий:
Рекомендуемые материалы
Для практической реализации требуется n считываний файла, что имеет большие временные затраты при большом объеме файла (N).
9.2. Случайная сортировка
Следующая процедура отбора приводит к простой случайной выборке:
1. Каждой единице совокупности присвоить случайное число (реализацию) u из равномерного распределения на отрезке [0,1]. Для этого можно воспользоваться генератором случайных чисел.
2. Ранжировать единицы в порядке убывания (или возрастания) присвоенных значений u.
3. Выбрать n первых единиц.
Доказательство.
Вероятность отбора выборки
равна:
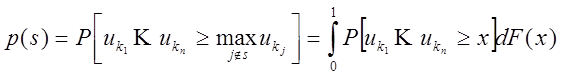
где F(x) - функция распределения 
:
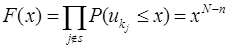
Поэтому
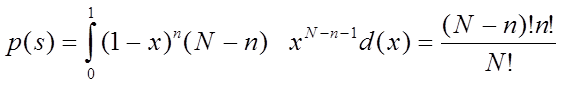
Комментарий :
- сортировка относительно долгая по времени при большом N;
- Однако этот метод позволяет делать несколько выборок без пересечения или с контролируемым пересечением списков единиц выборок.
9.3. Прямая реализация
1. Единицы совокупности, расположенные в случайном порядке или ранжированные по какому-либо признаку, пронумеровать значениями от 1 до N.
2. Получить n различных случайных чисел от 1 до N, в соответствии с законом равномерного распределения на {1,2, ..., N}.
3. Включить в выборку единицы с номерами, соответствующими значениям полученных случайных чисел.
Комментарий:
- требуется только одно считывание файла (в случае предварительного ранжирования полученных n случайных чисел);
- метод эффективен для небольших выборок;
- требует много времени для выборок большого объема (n).
9.4. Метод отбора-отказа
- независимые реализации случайной величины, полученные в соответствии с равномерным распределением на [0,1].
1. Если 
, то элемент k=1 извлекается, в противном случае - он пропускается.
2. Для k = 2, 3, ..., пусть j - число уже отобранных элементов (среди первых k-1 единиц).
Если 
, то элемент 
отбирается, в противном случае - пропускается.
3. Процедура заканчивается, когда j = n.
Доказательство:
Покажем рекуррентно, что 
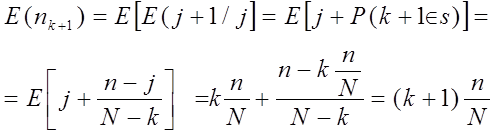
Значит:
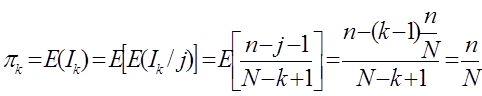
Но доказательство недостаточное!
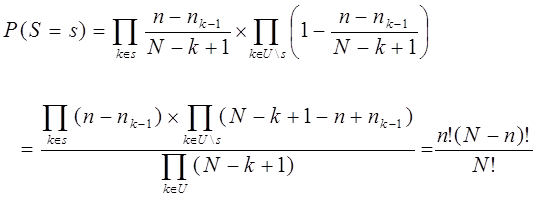
Комментарий:
требуется лишь одно считывание файла.
9.5. Актуализация выборки
Начинаем формирование выборки с n первых записей; затем этот первоначальный набор актуализируется, проверяя последовательно 
оставшихся единиц.
Алгоритм
Для 
:
1.Образовать случайное число u в промежутке от 0 до 1.
Если Вам понравилась эта лекция, то понравится и эта - 7 США в период президентства Эйзенхауэра 1952 - 1960.
2.Если 
: единица k вводится в выборку и заменяет уже существующую в ней единицу, определенную в результате равновероятностного извлечения среди n единиц выборки.
В противном случае, переходим к следующей единице.
Комментарий:
-не обязательно знать N заранее;
-требуется лишь одно считывание файла;
-отсутствует строгий критерий отбора заменяемых единиц.
