Вспомогательная информация и ее использование
Тема 3. Расслоенная случайная выборка
1. Вспомогательная информация и ее использование
Определение
Вспомогательной информацией называется априорное знание об исследуемой генеральной совокупности (U).
Это могут быть:
- значения некоторого вспомогательного признака (x) для всех единиц (U):
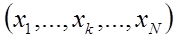
- функция этих величин, такая как суммарное значение:
Рекомендуемые материалы
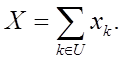
Вспомогательную информацию можно использовать для «улучшения»: 1) отбора; 2) оценки представляющего интерес параметра, рассчитанного на основе выборочных значений признака (y).
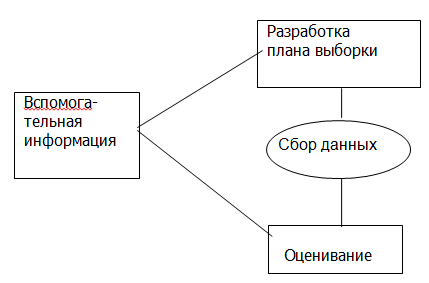
Рис. 1. Схема использования вспомогательной информации.
Цель – повысить точность оценивания, т.е оценить среднее или сумму с меньшей дисперсией.
Рассмотрим ситуацию, когда вспомогательная информация доступна на этапе разработки плана выборки.
В дисперсии оценки план выборки проявляется через вероятности включения элементов первого и второго порядков.
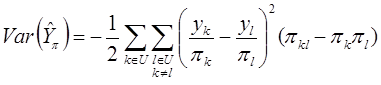
Существует две возможности оказать воздействие на дисперсию:
а) Повлиять на вероятности включения первого порядка:
можно положить вероятности извлечения единиц пропорциональными значениям признака (yk).
Тогда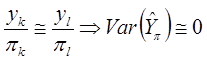 
Такой подход приводит к отбору с вероятностями пропорциональными размеру единиц.
б) Повлиять на вероятности включения второго порядка:
Положить значения 
малыми для больших отклонений 
. Например, для таких пар единиц совокупности можно положить 
. Это подразумевает их независимый отбор. Такой подход приводит к расслоенной случайной выборке.
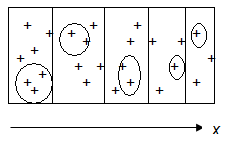
Принцип расслоения:
Если Вам понравилась эта лекция, то понравится и эта - Лекция 3.
· Расслаиваем совокупность (U) на H слоев 
, также называемых "стратами", так, чтобы в каждом h-ом слое дисперсия 
была бы по возможности небольшой;
· В каждом слое независимо осуществляем простой отбор единиц в выборку.
Замечание:
в отличие от простого случайного отбора этот метод требует наличия вспомогательных данных в основе выборки для целей расслоения.
Также предполагается, что объемы слоев 
известны.
