Метод сеток для уравнения параболического типа

Метод сеток для уравнения параболического типа.

В качестве примера уравнения параболического типа остановимся на уравнении теплопроводности для однородного стержня длиной :

                                                        (50)

где  - температура и  - время. Будем предполагать, что . То есть от уравнения (50) перейдем к уравнению

                                                            (51)

Пусть задано распределение температуры  в начальный момент времени  и законы изменения температуры в зависимости от времени на концах стержня  и :; . Требуется найти распределение температуры  вдоль стержня длиной  в любой момент времени . Функция  должна быть непрерывна и дважды непрерывно дифференцируема по своим переменным в области .

Область  заменим сеточной (Рис.14), разбивая ее с помощью шага  по  и с помощью шага  по . В результате замены непрерывной области  дискретным множеством узловых точек , исходная задача деформируется. Теперь будем искать решение  только на дискретном множестве . Т.е.  - двумерная таблица значений искомой функции в узловых точках.

Представим уравнение (51) в конечно-разностной форме, заменяя и  конечно-разностным аналогом в узловых точках :

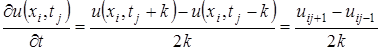
Рекомендуемые материалы

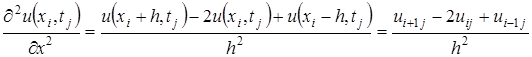
Получим конечно-разностный аналог исходной задачи: требуется найти значение функции , удовлетворяющего конечно-разностному уравнению вида:

,                   (52).

и дополнительным условиям:

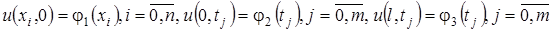
Получим систему линейных алгебраических уравнений, которую можно решить любым известным методом. Исследования показали, что значения  и  должны быть связаны между собой следующим образом: , где . Аппроксимируем уравнение (51) конечно-разностным

                                 (53)

Решая систему (53) с учетом дополнительных условий, получим  - искомую функцию в точках .

Второй вариант конечно-разностного аналога исходного дифференциального уравнения, т.н. явная схема, получается за счет того, что первые производные  в узловых точках  представлены в виде:

,

а вторая производная остается прежней. Получим исходное уравнение в конечно-разностной форме:

.

Считая, что , получим  или , . По этой формуле для каждого значения  для слоя  по оси  используются три значения  на предыдущем слое с номером . Для начала вычислений используем дополнительные условия.

В результате решения задачи в конечно-разностной форме мы получаем значения искомой функции в точках  (Рис.15), которые являются приближенным решением исходной задачи. На практике полагают , тогда расчетная формула упрощается и принимает следующий вид:

.

Данная расчетная формула дает наилучшее приближение к искомому решению, обеспечивая устойчивость конечно-разностной схемы и наилучшую аппроксимацию исходного уравнения конечно-разностным.

Заметим, что идея метода сеток, которая заключается в замене исходной области сеточной и замене исходной задачи конечно-разностным аналогом, используется при решении других типов уравнений в частных производных.

В случае неявной схемы используется другой вид аппроксимации и новое соотношение между шагами  и  в виде . Исходное дифференциальное уравнение (51) аппроксимируется конечно-разностным уравнением вида

Ещё посмотрите лекцию "Управление процессом паблик рилейшнз" по этой теме.

                                 (54)

Начальные и граничные условия остаются теми же, что в предыдущем случае. Для решения системы линейных алгебраических уравнений (54) применяется метод прогонки.

Суть метода прогонки состоит в том, что сначала вычисляются значения , выбирается значение  с целью получения требуемой скорости продвижения оси . Обозначим , , , . В прямом ходе на очередном  временном слое вычисляются вспомогательные функции:

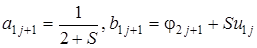
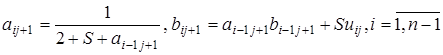
В обратном ходе вычисляются значения искомой функции на  слое по формуле . Величина  является значением искомой функции в точке , а  - в точке . Погрешность метода . Из анализа устойчивости неявной схемы вытекает, что следует назначать .