Метод сеток для уравнений гиперболического типа

Метод сеток для уравнений гиперболического типа.

Рассмотрим свободные колебания однородной ограниченной струны длины (). Поперечное сечение  при  для любого момента времени  удовлетворяет уравнению гиперболического типа вида:

                                                      (55)

где , и будем искать решение уравнения (55) при заданных начальных и краевых условиях:

, , при                             (56)

 при                                (57)

Решим эту задачу методом сеток. Как и в случае параболического уравнения, заменим прямоугольную область  и  сеточной , где , , . Шаг по оси  - , шаг по оси  - .

На сетке  приближенно заменим дифференциальное уравнение (55) конечно-разностным аналогом:

Люди также интересуются этой лекцией: РУБЛЁВ Андрей.

                            (58)

При  уравнение (58) упрощается и принимает вид:

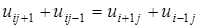
откуда

                                     (59)

Из уравнения (59) видно, что для получения значений  в -м слое используются значения  в двух предыдущих слоях -м и -м. Для начала вычислений по формуле (59) также необходимо знать значения и  на нулевом слое . Используя начальное условие , можно определить значения  на фиктивном слое с номером . Для этого заменим производную в условии конечно-разностным соотношением: , где . Отсюда находим . Зная значения  на слое , можно начать вычисления. Краевые условия (59) используются для получения значений  и .