Дифференциалы высших порядков

Дифференциалы высших порядков

            Общая теория производных высших порядков (или высших производных) в многомерном анализе весьма сложна и выходит за рамки нашего курса. Сложность этой теории обусловлена тем, что - в существенном отличии от одномерного анализа -  производная функция векторной функции есть функция, принимающая значения совсем в другом линейном пространстве, а именно в пространстве линейных операторов, действующих из  в (см. п. 2.4). Следовательно, производная этой функции, т.е. производная второго порядка, есть функция, принимающая значения в пространстве линейных операторов, действующих из пространства  в пространство линейных операторов, действующих из  в . Тогда построение теории высших производных требует рассмотрения сложной иерархии линейных пространств. Мы оставляем эти рассмотрения за рамками наших лекций. Здесь мы введем только понятие дифференциала второго и более высокого порядков для числовой функции.

            Коль скоро первый дифференциал функции , как было замечено в п. 2.5, есть функция точки

            ,                                                    (1)

можно поставить вопрос об ее дифференцируемости. Предполагая условия дифференцируемости выполненными, найдем первый дифференциал от выражения (1). Вычисляя этот дифференциал, мы, во-первых, используем формулу для дифференциала произведения двух функций:  (это предлагается доказать читателю); во-вторых, мы считаем приращения  независимых переменных  не зависящими от точки . Это предположение разумно, если рассматривать указанные переменные действительно как независимые - тогда в любой точке приращения переменных могут быть выбраны как угодно. Заметим, что отказ от этого предположения, т.е. рассмотрение переменных как функций, в свою очередь зависящих от некоторых переменных, существенно меняет получаемый результат (свойство инвариантности формы перестает выполнятся).

            Дифференцируем (1):

            (2)         

Так как (согласно нашему второму предположению) все , то получаем:

                                             (3)

Рекомендуемые материалы

            Внутренняя сумма в (3) есть первый дифференциал частной производной . Выражение (3)  называется дифференциалом второго порядка (или вторым дифференциалом) функции в точке и обозначается . Его можно записать несколько проще:

                                              (4)

            Коэффициенты в двойной сумме (4) - это всевозможные частные производные второго порядка вида , вычисленные в текущей точке  (указание на которую мы будем часто опускать). Эти производные обычно записываются в виде:

            .

            Вторые производные образуют квадратную матрицу -ого порядка, называемую матрицей Гессе функции . Как и матрица Якоби, матрица Гессе есть функция точки. В общем случае матрица Гессе не является симметричной, т.е. в общем случае значение второй производной зависит от порядка дифференцирования: . Но имеет место следующее утверждение, известное под названием леммы Шварца:

            Утверждение 2.11 (лемма Шварца). Если производные  непрерывны в некоторой окрестности точки , то .

            Доказательство опускается.

            Итак, в случае непрерывности «смешанных» производных второго порядка их значение не зависит от порядка дифференцирования, и матрица Гессе симметрична. В дальнейшем, как правило, мы предполагаем, что условия леммы Шварца выполняются. Тогда второй дифференциал можно рассматривать как квадратичную форму от приращений независимых переменных,  матрицей которой является  матрица Гессе.

            (По умолчанию, напомним, считается фиксированным канонический базис пространства ).

            Вернемся теперь к равенствам (2) и допустим, что переменные  сами суть функции от некоторых переменных . Обозначая , получим, что . Тогда из (2) следует

                 (5)

            Таким образом, во втором дифференциале сложной функции (в (5)) появляется дополнительное слагаемое, учитывающее вторые дифференциалы функций, от которых непосредственно зависит анализируемая сложная функция. Это значит, что второй дифференциал не обладает свойством инвариантности формы.

            Дифференциалы третьего и более высоких порядков могут быть далее определены согласно формуле:

            Можно доказать индукцией, что -ый дифференциал представляется в виде суммы:

 .       (6)

При (первый дифференциал) выражение (6) есть линейная (1-) форма, при  (второй дифференциал) - квадратичная (2-)форма. В общем случае это выражение называется степенной (-) формой от переменных  . Коэффициенты в сумме (6), содержащей, очевидно, слагаемых, называются частными производными порядка  функции . По определению

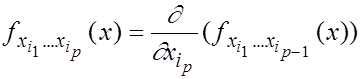
Бесплатная лекция: "Приложение Д Обратные матрицы" также доступна.

Эта производная обозначается также и как . В случае непрерывности этих производных их значение не зависит от порядка дифференцирования.

            Определение 2.23. Функция называется функцией класса  (записывают ), если она имеет в каждой точке множества все дифференциалы до -ого включительно, причем дифференциал непрерывен в каждой точке множества .

            Нетрудно понять, что при  мы получим непрерывно дифференцируемую на функцию, т.е. функцию класса (определения 2.17 и 2.18, п. 2.6).

                        Функцию класса  называют также гладкой функцией класса гладкости  (на множестве ). Говорят, что функция есть функция класса гладкости ¥, если она принадлежит множеству  для каждого (это записывают еще так: ). Такую функцию называют также просто гладкой.

            Поверхность , где , называют гладкой поверхностью класса гладкости , если , где - область определения функции . Если , то указанная поверхность называется просто гладкой. При  получаем гладкую кривую.

            Практически все поверхности и кривые, которые мы рассматриваем, являются гладкими - таковы, в частности, все линейные многообразия и поверхности второго порядка.