Приложение Д Обратные матрицы
П.5. Обратные матрицы
Квадратная матрица полного ранга является невырожденной. Невырожденная матрица А имеет единственную обратную матрицу A–1 с которой выполняются следующие равенства
АA–1=A–1А=I (П.5.1)
Если квадратная матрица А не имеет полный ранг, то она не имеет обратной матрицы и является вырожденной. Заметим, что прямоугольные матрицы полного ранга не имеют единственных обратных. Из выражения (П.5.1) следует, что обратной матрицей для A–1 является А, то есть,
(A–1)–1=A. (П.5.2)
Пример П.5. Пусть A=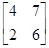 , тогда A–1=
, тогда A–1=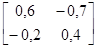 и
и
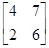
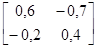 =
=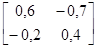
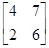 =
=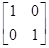
□
В приложениях обратные матрицы обычно находятся с использованием компьютера. Многие калькуляторы также вычисляют обратные матрицы. Алгоритмы расчета обратных небольших матриц можно найти в книгах по матричной алгебре.
Рекомендуемые материалы
Если матрица B невырожденная и AB=CB, то можно умножить обе части этого уравнения справа на B–1 и получить A=C. (Если В вырожденная или прямоугольная, то матрицу В в AB=CB невозможно сократить с обеих сторон, см. пример П.4.2 и абзац перед примером.) Аналогично, если А невырожденная, то система уравнений Ах=с имеет единственное решение, так как обе её части можно умножить слева на A–1 и получить
A–1Ах=A–1с
x=A–1c. (П.5.3)
Два свойства обратных матриц приведены в следующих теоремах.
Теорема П.5.1. Если матрица А невырожденная, то AТ тоже невырожденная и обратную ей матрицу можно найти из выражения
(AТ)–1=(A–1)Т (П.5.4)
Доказательство: Матрица AТ невырожденная по определению, так как её строки являются столбцами матрицы А. Чтобы показать, что (AТ)–1=(A–1)Т, транспонируем обе части равенства AA–1=I и получим (AA–1)Т=IТ или (A–1)ТAТ=I. Умножая обе части справа на (AТ)–1 получаем требуемый результат.
□
Теорема П.5.2. Если А и В невырожденные матрицы одинаковых размеров, то AB невырожденная и
(AB)–1=B–1A–1 (П.5.5)
Доказательство: По пункту 2 теоремы П.4 матрица (AB)–1 существует. Тогда
AB(AB)–1=I,
A–1AB(AB)–1=A–1,
B–1B(AB)–1=B–1A–1,
(AB)–1=B–1A–1.
□
Рассмотрим теперь обратные матрицы некоторых специальных матриц. Если симметричная и невырожденная матрица А разделена на подматрицы в виде
А=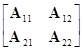
и если B=A22–A21A11–1A12, то при условии существования A11–1 и B–1 обратная матрицы А задается выражением
A–1= . (П.5.6)
. (П.5.6)
В качестве применения выражения (П.5.6) найдём обратную матрицу симметричной невырожденной матрицы
А= ,
,
где A11 - квадратная матрица, a22 - скаляр и a12 - вектор. Если существует A11–1, то матрицу A–1 можно представить в виде
A–1= , (П.5.7)
, (П.5.7)
где b=a22–a12ТA11–1a12.
Другим случаем применения выражения (П.5.6) является
 =
= . (П.5.8)
. (П.5.8)
Если квадратная невырожденная матрица вида B+ccТ, где с - вектор и B - невырожденная матрица, то
(B+ccТ)–1=B–1–B–1ccТB–1(1+cТB–1c)–1 (П.5.9)
[Abadir, Magnus (2005) стр.87, 248]. Это проверяется умножением. Пусть b=(1+cТB–1c)–1, тогда
(B+ccТ)(B+ccТ)–1=(B+ccТ)(B–1–B–1ccТB–1b)
=BB–1–BB–1ccТB–1b+ccТB–1–c(cТB–1c)cТB–1b
=I–(b–1+bcТB–1c)ccТB–1
=I–(b+bcТB–1c–1)ccТB–1
=I,
так как квадратичная форма cТB–1c является просто числом и b(1+cТB–1c)=1.
В более общем виде, если матрицы A, B и А+PBQ невырожденные, то
(А+PBQ)–1=А–1–А–1РB(B+BQА–1РB)–1BQА–1 (П.5.10)
Это выражение также проверяется умножением
(А+PBQ)[А–1–А–1РB(B+BQА–1РB)–1BQА–1]
=АА–1+PBQА–1–АА–1РB(B+BQА–1РB)–1BQА–1–PBQА–1РB(B+BQА–1РB)–1BQА–1
=I+P[I–B(B+BQА–1РB)–1–BQА–1РB(B+BQА–1РB)–1]BQА–1
=I+P[I–(B+BQА–1РB)(B+BQА–1РB)–1]BQА–1
=I+P[I–I]BQА–1
=I.
П.6. Определённые матрицы
Квадратичная форма была определена выражением (П.2.25). Например, квадратичная форма 3y12+y22+2y32+4y1y2+5y1y3–6y2y3 может быть записана в виде уТАу, где
у= и А=
и А= .
.
Однако ту же квадратичную форму можно представить с симметричной матрицей получаемой из исходной А по формуле
(А+АТ)/2= .
.
В общем, любая квадратичная форма уТАу может быть представлена в виде
уТАу=уТ[(А+АТ)/2]у. (П.6.1)
Поэтому матрица квадратичной формы всегда может быть выбрана так, чтобы быть симметричной и, следовательно, однозначно определённой.
Встречаемые в регрессии и дисперсионном анализе суммы квадратов могут быть представлены в виде квадратичной формы уТАу, где у - вектор результатов наблюдений. Такие квадратичные формы остаются положительными (или, по крайней мере, неотрицательными) для всех возможных значений элементов вектора у. Рассмотрим теперь квадратичные формы этого типа.
Если симметричная матрица А удовлетворяет условию уТАу>0 то для всех возможных у≠0 квадратичная форма уТАу является положительно определённой и входящая в неё матрица А тоже положительно определённая. Если же уТАу<0, то для всех возможных у≠0 квадратичная форма уТАу является отрицательно определённой и входящая в неё матрица А тоже отрицательно определённая.
Аналогично, если уТАу≥0 для всех у и есть по крайней мере один вектор у≠0 такой, что уТАу=0, то квадратичная форма уТАу и матрица А неотрицательно определённые. Если же уТАу≤0 для всех у и есть по крайней мере один вектор у≠0 такой, что уТАу=0, то квадратичная форма уТАу и матрица А неположительно определённые.
Положительно и неотрицательно определённые матрицы показаны в следующем примере.
Пример П.6. В качестве примера положительно определённой матрицы рассмотрим
А=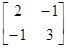
и связаную с ней квадратичную форму
уТАу=2у12–2у1у2+3у22=2(у1–у2/2)2+5у22/2,
которая явно положительна если у1 и у2 не равны нулю.
В качестве примера неотрицательно определённой матрицы возмём выражение
(2у1–у2)2+(3у1–у3)2+(3у2–2у3)2,
которое может быть представлено в виде квадратичной формы уТАу с матрицей
А= .
.
Если 2y1=y2, 3y1=y3 и 3y2=2y3, то (2y1–y2)2+(3y1–y3)2+(3y2–2y3)2=0. Таким образом, уТАу=0 для любого вектора у, значения элементов которого соответствуют уравнениям 2y1=y2, 3y1=y3 и 3y2=2y3, например, уТ= [1, 2, 3]. В противном случае уТАу>0 (кроме, у=0).
□
В матрицах примера П.6 диагональные элементы положительные числа. В общем, для положительно определённых матриц это справедливо.
Теорема П.6.1.
- Если матрица А положительно определённая, то все её диагональные элементы aii положительные.
- Если матрица А неотрицательно определённая, то все aii ≥0.
Доказательство:
- Пусть уT= [0,..., 0, 1, 0,..., 0] с 1 в i-й позиции и 0 в остальных. Тогда уТАу=aii >0.
- Пусть уT= [0,..., 0, 1, 0,..., 0] с 1 в i-й позиции и 0 в остальных. Тогда уТАу=aii ≥0.
□
Некоторые дополнительные свойства положительно и неотрицательно определённых матриц даны в следующих теоремах.
Теорема П.6.2. Пусть Р - невырожденная матрица.
- Если А положительно определённая, то и PТАР положительно определённая.
- Если А неотрицательно определённая, то и PТАР неотрицательно определённая.
Доказательство:
- Чтобы показать, что уТPТАРу >0 при у≠0, заметим, что уТ(PТАР)у=(Ру)ТA(Ру). Так как А положительно определённая, то (Ру)ТA(Ру)>0, при условии, что Ру≠0. В силу (П.5.3), Ру=0 только если у=0, так как P–1Py=y=0. Отсюда, если у≠0, то уТPТАРу>0.
- Доказательство аналогично проведённому в пункте 1, где знак > необходимо заменить на ≥.
□
Следствие 1. Пусть матрицы А=Aпп положительно определённая и В=Вkп - любая матрица ранга k ≤ п. Тогда матрица BABТ положительно определённая.
Доказательство: Квадратичная форма уТBABТу=(BТу)ТA(BТу)>0, если BТу≠0, так как А положительно определённая. Вектор BТу=у1b1+y2b2+…+ykbk, где b1, b2,…, bk – столбцы матрицы BТ или строки матрицы В. Так как матрица В ранга k, то её строки линейно независимы и не существует такого ненулевого вектора у чтобы BТу=0.
□
Следствие 2. Пусть матрица А=Aрр положительно определённая и В=Вkр - любая. Если k > р или ранг(B)=r, где r <k и r <р, то матрица BABТ неотрицательно определённая.
Доказательство: Подобно доказательству следствия 1.
□
Теорема П.6.3. Симметричная матрица А положительно определённая, если и только если существует невырожденная матрица P такая, что А=PТР.
Доказательство: Докажем часть «если». Для невырожденной матрицы P пусть А=PТР. Тогда
уТАу=уТPТРу=(Ру)Т(Ру)
это произведение вектора на себя или сумма квадратов является положительной, кроме случая Ру=0. В силу (П.5.3), равенство Ру=0 соблюдается, только если у=0.
В части «только если» докажем, что если А положительно определённая, то А=PТР, где Р невырожденная. По теореме П.12.4 имеем A=MLMT, где M ортогональная и L=диаг[l1, l2, …, ln] со всеми li>0. В силу (П.12.17) и (П.12.18), A=MLMT=ML1/2L1/2MT =(L1/2MT)T(L1/2MT)=PТР, где L1/2=( ,
,  , ...,
, ...,  ). Матрица L1/2 и ортогональная матрица невырожденные, поэтому по теореме П.5.2 матрица Р=L1/2MT невырожденная.
). Матрица L1/2 и ортогональная матрица невырожденные, поэтому по теореме П.5.2 матрица Р=L1/2MT невырожденная.
□
Следствие 1. Любая положительно определённая матрица является невырожденной.
Доказательство: Это следует из теоремы П.6.3 и пункта 2 теоремы П.4.
□
Один из методов представления положительно определенной матрицы А в виде произведения PТР, как в теореме П.6.3, обеспечивается разложением Холецкого [Seber, Lee (2003) стр.335-337] с помощью которого можно однозначно разложить матрицу А в виде A=TTT, где T - невырожденная верхняя треугольная матрица.
Для любой квадратной или прямоугольной матрицы B матрица BTB положительно или неотрицательно определённая.
Теорема П.6.4. Пусть матрица В=Вnр имеет р ≤ n. Тогда:
- Если ранг(B)=р, то матрица BTB положительно определённая.
- Если ранг(B) < р, то матрица BTB неотрицательно определённая.
Доказательство:
- Чтобы показать, что уТBTBу >0 при у≠0, заметим, что
уТBTBу=(Bу)Т(Bу)
является суммой квадратов и поэтому положительна, за исключением когда Bу=0. В силу (П.3.3), Bу можно представить в виде
Bу=y1b1+y2b2+...+ypbp.
Эта линейная комбинация не равна 0 (для любого у≠0), так как ранг(B)=p и, следовательно, столбцы матрицы B линейно независимы.
- Если ранг(B) < p, то можно найти такой вектор у≠0, что
Bу=y1b1+y2b2+...+ypbp=0,
так как столбцы матрицы B линейно зависимы [см. (П.4.1)]. Поэтому уТBTBу≥0.
□
Заметим, что если матрица B квадратная, то матрица BB=B2 необязательно будет неотрицательно определённой. Например, пусть
B= , тогда B2=BB=
, тогда B2=BB= и BTB=
и BTB= .
.
В этом случае, B2 не является неотрицательно определённой, но BTB - неотрицательно определённая, так как уТBTBу=2(y1–2y2)2.
Следствие 1. Матрица BBT положительно определённая, если В имеет полный ранг по строкам, в противном случае матрица BBT - неотрицательно определённая.
□
Два дополнительных свойства положительно определённых матриц даны в следующих теоремах.
Теорема П.6.5. Если матрица А положительно определённая, то и A–1 положительно определённая.
Рекомендуем посмотреть лекцию "4.5 Период дворцовых переворотов".
Доказательство: По теореме П.6.3 имеем A=РTР, где Р - невырожденная матрица. С учётом теорем П.5.1 и П.5.2, получаем A–1=(РTР)–1=P–1(РT)–1=P–1(P–1)T. По теореме П.6.3 эта матрица положительно определённая.
□
Теорема П.6.6. Если матрица А положительно определённая и разделена на подматрицы в виде
А=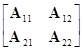 ,
,
где подматрицы A11 и A22 квадратные, то они положительно определённые.
Доказательство: Матрицу A11 можно записать, например, в виде A11=[В, O]A , где В тех же размеров, что и A11. Тогда по следствию 1 теоремы П.6.2, матрица A11 положительно определённая.
, где В тех же размеров, что и A11. Тогда по следствию 1 теоремы П.6.2, матрица A11 положительно определённая.






















