Приложение Г Ранг матрицы

П.4. Ранг матрицы

Перед определением ранга матрицы введём понятие линейной зависимости и независимости векторов. Совокупность векторов а₁, а₂, …, а_m называется линейно зависимой, если можно найти наборы не равных нулю скалярных чисел с₁, с₂,..., с_m, для которых выполняется равенство

с₁а₁+с₂а₂+…+с_mа_m=0.                                               (П.4.1)

При этом нулевой вектор 0 раскладывается неединственным образом в линейную комбинацию векторов а₁, а₂, …, а_m. Но, если нулевой вектор 0 раскладывается в линейную комбинацию ненулевых векторов а₁, а₂, …, а_n единственным образом, то есть, только когда с₁=с₂=…=с_m=0, то эта совокупность векторов называется линейно независимой [Беклемишев (2006) стр.13].

В силу (П.3.3), линейную независимость ненулевых столбцов матрицы А можно определить следующим образом. Столбцы матрицы А линейно независимы, если равенство Ас=0 означает, что вектор с=0. Если хотя бы один столбец матрицы А является нулевым вектором, то все её столбцы линейно зависимы. Поэтому матрица, в которой столбцы (или строки) линейно зависимы, называется вырожденной. Единичная матрица является невырожденной.

В матрице А=А_пр квадратная подматрица размеров rxr или порядка r называется базисной, если она невырожденная, а все существующие квадратные подматрицы больших размеров - вырожденные. Рангом матрицы называется порядок её базисной подматрицы или наибольший порядок её невырожденных квадратных подматриц и обозначается ранг(А). Число линейно независимых столбцов любой матрицы всегда равно числу линейно независимых её строк, то есть, ранг любой матрицы равен её строчному рангу и её рангу по столбцам [Беклемишев (2006) стр.133].

Если матрица А имеет один ненулевой элемент со всеми другими элементами равными 0, то ранг(A)=1. Ранг вектора 0 и матрицы O равен 0.

Положим, что прямоугольная матрица А=А_пр ранга р, где р<n. В этом случае матрица А имеет максимально возможный ранг и говорят, что она полного ранга по столбцам или имеет полный ранг по столбцам. В общем, максимально возможный ранг матрицы А=А_пр равен минимальному значению n или р. Поэтому в прямоугольной матрице строки или столбцы (или оба) линейно зависимы. Покажем это на следующем примере.

Пример П.4.1. Ранг матрицы А=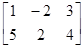 равен 2 потому, что две строки линейно независимы (нет такого числа умножение на которое превращало бы одну строку в другую). Следовательно, по определению ранга, число линейно независимых столбцов также равно 2. Таким образом столбцы матрицы А линейно зависимы и существуют такие постоянные с₁, с₂ и с₃, что

Рекомендуемые материалы

с₁+с₂+с₃=.

В силу (П.3.3) это уравнение можно записать в виде

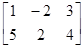
= или Ас=0                           (П.4.2)

Решением уравнения (П.4.2) является вектор с^Т= [14, –11, –12]. Здесь произведение Ac=0 несмотря на то, что A≠O и с≠0. Это получается потому, что столбцы матрицы А линейно зависимы.

□

Уравнение (П.4.2) применимо и для произведения матриц. Можно найти матрицы A≠O и B≠O такие, что

AВ=O,                                                                       (П.4.3)

например,

=.

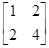
Можно использовать также линейные зависимости строк или столбцов матриц для создания таких выражений как АВ=СВ, где А≠С. Поэтому в матричном уравнении, в общем, нельзя сокращать матрицу с обеих его сторон. Но существуют два исключения из этого правила:

1. Если B - квадратная матрица полного ранга, то AB=CB означает А=C;
2. Другой особый случай возникает, когда выражение справедливо для всех возможных значений общей для обеих сторон уравнения матрицы, например,

если Ах=Вх для всех возможных значений х,                            (П.4.4)

то А=В. Чтобы убедиться в этом, пусть х^Т= [1, 0, ..., 0]. Тогда, в силу (П.3.3), первый столбец матрицы А равен первому столбцу матрицы B. Пусть теперь х^Т= [0, 1, 0, ..., 0], и второй столбец матрицы А равен второму столбцу матрицы B. Продолжая таким образом, получим A=B.

Пример П.4.2. Покажем существование матриц A, B и С таких, что АВ=СВ, где A≠C. Пусть

А=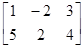,        В=,     С=.

Тогда

АВ=СВ=.

Лекция "Особенности использования операций ++ и --" также может быть Вам полезна.

□

Следующая теорема дает общий случай и два частных случая для ранга произведения двух матриц.

Теорема П.4

1. Если матрицы А и В имеют соответствующие размеры для умножения, то ранг(AB)≤ ранг(А) и ранг(AB)≤ ранг(B).
2. Умножение А на квадратную матрицу полного ранга не меняет её ранг, то есть, если B и C квадратные матрицы полного ранга, то ранг(AB)=ранг(CA)=ранг(А).
3. Для любой матрицы А, ранг(A^ТA)=ранг(АА^Т)=ранг(А^Т)=ранг(А).

Доказательство:

1. Все столбцы AB являются линейными комбинациями столбцов матрицы А (см. комментарий после примера П.3). Следовательно, число линейно независимых столбцов AB меньше или равно числу линейно независимых столбцов A, и ранг(АВ) ≤ ранг(А). Точно так же, все строки AB являются линейными комбинациями строк B [см. комментарий после (П.3.4)] и, следовательно, ранг(AB)≤ ранг(B).
2. Если матрица B квадратная (невырожденная) и полного ранга, то существует такая её обратная матрица B^–1, что BB^–1=I. Тогда по пункту 1 имеем

ранг(A)=ранг(ABB^–1) ≤ ранг(AB) ≤ ранг(А).

Таким образом, оба неравенства обращаются в равенства и ранг(A)=ранг(AB). Аналогично, ранг(A)=ранг(CA) для невырожденной матрицы C.

1. Если принять А^Т=C или А^Т=В, то доказательство следует из пункта 2. А транспонирование любой матрицы не меняет её ранга, так как число линейно независимых строк и столбцов остаётся прежним.