Независимость линейных и квадратичных форм

5.6. Независимость линейных и квадратичных форм

В этом разделе обсуждается статистическая независимость линейной и квадратичной форм, двух квадратичных форм и нескольких квадратичных форм. В качестве примеров независимости линейной и квадратичной форм могут рассматриваться усреднённое  и выборочная дисперсия s² простой случайной выборки или оценка  параметра линейной модели и выборочная дисперсия s². Примером независимости двух квадратичных форм является независимость регрессионной суммы квадратов и суммы квадратов остаточных ошибок. Примером независимости нескольких квадратичных форм могут служить суммы квадратов благодаря главным эффектам и взаимодействиям в сбалансированном двухфакторном анализе дисперсии.

Рассмотрим статистическую независимость линейной и квадратичной форм.

Теорема 5.6.1. Пусть вектор у имеет нормальное распределение N_п(y, S), матрица B некоторых числовых значений размеров kхп, а матрица A некоторых числовых значений симметричная и размеров пхп. Тогда линейная форма Ву и квадратичная форма у^TAy распределены независимо, если и только если BSA=O.

Прежде чем доказывать теорему сделаем два примечания. Для применения этой теоремы квадратичная форма у^TAy не должна иметь нецентральное распределение c². Эта теорема не рассматривает произведение ASB, которого может не существовать. При доказательстве следуем [Searle (1971) стр.59].

Докажем достаточность, что BSA=О означает независимость Ву и у^TAy.

Так как матрица А симметричная, то по теореме П.12.9 она может быть представлена так А=LL^T, где L - некоторая матрица полного ранга по столбцам. Следовательно, если BSA=О, то и BSLL^T=О. Так как L имеет полный ранг по столбцам, то существует (L^TL)^–1 [см. пункт 1 теоремы П.2.3] и поэтому, умножив BSLL^T=О справа сначала на L, а затем на (L^TL)^–1, получаем

BSLL^TL(L^TL)^–1=О, то есть BSL=О.

Следовательно, ковариация векторов By и (y^TL)^T принимает значение

Рекомендуемые материалы

С[(By, (y^TL)^T]=Е[(Вy–Вy)(L^Ty–L^Ty)^T]

=Е[В(y–y)(y–y)^TL]

=BSL=О.

Так как у - вектор нормально распределенных переменных, то по следствию 2 теоремы 4.5.4 векторы Ву и (y^TL)^T=L^Ty распределены независимо друг от друга. Следовательно, Bу и квадратичная форма у^TAу=у^TLL^Tу, являющаяся непрерывной функцией вектора L^Ty, распределены независимо [Себер (1980) стр. 26, 40-41].

Докажем необходимость, что независимость у^TAу и Ву означает BSA=О.

Если у^TAу и Ву статистически независимы, то С(Bу, у^TAу)=0 и по следствию 1 теоремы 5.2.4 имеем С(Bу, у^TAу)=2BSAy. Следовательно, 2BSAy=0 и, так как это верно для любых значений вектора y, то BSA=O. Доказательство теоремы закончено.

□

Пример 5.6.1. Если матрица А симметричная и идемпотентная, то независимость Ву и у^TAy доказывается проще.

Положим, что BSA=O. Если А симметричная и идемпотентная, то у^TAy можно записать в виде произведения двух векторов

у^TAy=у^TA^TАy=(Ay)^TAy.

Если BSA=O, то, в силу (3.6.11),

BSA=С(Ву, Ау)=O.

Поэтому по следствию 2 теоремы 4.5.4 векторы Ву и Ау независимы, и следовательно Ву и (Ay)^TAy, как непрерывная функция вектора Ay, также независимы [Себер (1980) стр. 26, 40-41].

Докажем теперь обратное, а именно, если Ву и у^TAy независимы, то BSA=O. В силу следствия 1 теоремы 5.2.4, имеем C(By, y^TAy)=2BSAy и при независимости Ву и у^TAy получаем С(Ву, у^TAy)=0. Отсюда выходит, что

2BSAy=0.

Поскольку это верно для всех возможных значений вектора y, то в силу (П.4.4), равенство 2BSAy=Оy подтверждает BSA=O.

□

Обратим внимание, что BSA=O не значит ASB=O. В самом деле, произведение ASB не будет определено, если B не имеет п строк.

Следствие 1. Когда у ~ N_п(y, s²I), то Ву и у^TAy распределены независимо, если и только если BA=O.

Доказательство: BSA=B(s²I)A=s²BA, что равно О, если BA=O.

□

Пример 5.6.2. Для применения следствия 1 рассмотрим s²= и =, где вектор у^T=[y₁, y₂, ..., у_n] распределен в виде N_n(y1, s²I). Как и в примере 5.1, статистики  и s² можно записать в виде =1^Tу/n и s²=y^Т(I–E/n)y/(n–1). По следствию 1 усреднённое  не зависит от выборочной дисперсии s², так как (1/n)1^T(I–E/n) =0^T.

□

Следующая теорема о независимости двух квадратичных форм подобна только что рассмотренной теореме 5.6.1 и ее доказательство следует той же схеме.

Теорема 5.6.2. Пусть А и В симметричные матрицы некоторых числовых значений. Если вектор у имеет нормальное распределение N_п(y, S), то квадратичные формы у^TAy и у^TВy распределены независимо, если и только если ASB=O (или, что то же самое, BSA=О).

Заметим, что законы распределений квадратичных форм у^TAy и у^TВy в этой теореме не указаны. Она справедлива независимо от того какие распределения имеют эти квадратичные формы. Условие только одно, что вектор у случайных переменных распределён по нормальному закону. На практике эта теорема обычно применяется в ситуациях, где квадратичные формы имеют распределения c², как определено теоремой 5.5, но это не является обязательным условием применения теоремы 5.6.2. При доказательстве следуем [Searle (1971) стр. 59-60].

Доказательство: Условие ASB=О эквивалентно условию BSA=О, так как матрицы А, B и S симметричные. Следовательно, каждое условие подразумевает другое.

Докажем достаточность, что ASB=О означает независимость у^TAy и у^TВy.

Так как матрицы А и В симметричные, то по теореме П.12.9 можно написать A=LL^T и B=СС^T, где матрицы L и С имеют полный ранг по столбцам. Таким образом, если ASB=О, то LL^ТSСС^Т=О. Так как существуют обратные матрицы (L^TL)^–1 и (С^TС)^–1, то умножая LL^ТSСС^Т=О слева на L^Т и справа на С, а затем слева на (L^TL)^–1 и справа на (С^TС)^–1, получаем L^TSС=О. Ковариация векторов L^Tу и (у^TС)^T

С[L^Tу, (у^TС)^T]=Е[(L^Ty–L^Ty)(С^Tу–С^Ty)^T]

=L^TЕ[(y–y)(у–y)^T]С

=L^TSС=О.

Отсюда, так как у - вектор нормально распределенных переменных, то L^Tу и (у^TС)^T=С^Tу распределены независимо друг от друга. Следовательно, непрерывные функции у^TAу=у^TLL^Tу и Bу=у^TССу^T соответственно векторов L^Tу и С^Tу распределены независимо [Себер (1980) стр. 26, 40-41].

Докажем необходимость, что независимость у^TAy и у^TВy означает ASB=О.

Когда квадратичные формы у^TAy и у^TВy распределены независимо, то их ковариация С(x^TAx, x^TBx)=0, так что

D(у^TAy+у^TВy)=D(у^TAy)+D(у^TВy),

то есть,

D[y^T(A+B)y]=D(у^TAy)+D(у^TВy).

Использование выражения (5.2.6) для преобразования трёх членов этого уравнения после показанного ниже небольшого упрощения

2след{[(A+B)S]²}+4y^T(A+B)S(A+B)y=2след[(AS)²]+4y^TASAy+2след[(BS)²]+4y^TBSBy.

2след[(AS+BS)²]+4y^T(AS+BS)(A+B)y=2след[(AS)²]+4y^TASAy+2след[(BS)²]+4y^TBSBy.

2след[(AS)²+2ASBS+(BS)²]+4y^T(AS+BS)(A+B)y

=2след[(AS)²]+4y^TASAy+2след[(BS)²]+4y^TBSBy.

2след[(AS)²]+2след[2ASBS]+2след[(BS)²]+4y^T(AS+BS)(A+B)y

=2след[(AS)²]+4y^TASAy+2след[(BS)²]+4y^TBSBy.

2след[2ASBS]+4y^TASAy+4y^TBSAy+4y^TASBy+4y^TBSBy=4y^TASAy+4y^TBSBy

приводит к выражению

след(ASBS)+2y^TASBy=0.                                     (5.6.1)

Оно верно для всех значений вектора y, включая y=0, что приводит к след(ASBS)=0 и, подставляя это обратно в (5.6.1) получаем 2y^TASBy=0. Полученное равенство верно для всех значений вектора y и, так как y^TASBy=y^TОy, то ASB=О. Этим теорема доказана.

□

Следствие 1. Если вектор у имеет нормальное распределение N_п(y, s²I), то у^TAy и у^TВy статистически независимы, если и только если AB=O (или, что то же самое, ВА=O).

Доказательство: ASB=A(s²I)B=s²AB, что равно O, если AB=O.

□

Пример 5.6.3. Если матрицы А и В симметричные и идемпотентные, то независимость у^TAy и у^TВy доказывается проще. Положим, ASB=O. Так как А и В симметричные и идемпотентные, то квадратичные формы у^TAy и у^TВy можно записать в виде у^TAy=у^TA^TAy=(Ay)^TAy и у^TВy=y^TB^TВy=(Вy)^TВy. Так как ASB=O, то, в силу (3.6.11),

ASB=С(Ay, By)=O.

Поэтому по следствию 2 теоремы 4.5.4 векторы Ay и By независимы. Отсюда следует, что непрерывные функции (Ay)^TAy=у^TAy и (Вy)^TВy=у^TВy этих векторов тоже независимы [Себер (1980) стр.26, 40-41].

□

Заметим, что ASB=O эквивалентно BSA=O с перестановкой обеих сторон ASB=O дает BSA=O (матрицы A и B симметричные).

Пример 5.6.4. Применяя следствие 1 теоремы 5.6.2, рассмотрим разложение суммы квадратов =+n, которое выражением (5.1.3) представлено в виде квадратичных форм

y^ТIy=y^Т(I–Е/n)y+y^Т(Е/n)y.

Когда вектор у~N_п(y1, s²I), то по следствию 1 квадратичные формы y^Т(I–E/n)y и y^Т(E/n)y независимы, если и только если (I–E/n)(E/n)=О, что и показано в разделе 5.1.

□

Прежде чем перейти к заключительной теореме о статистической независимости нескольких квадратичных форм, напомним, что теоремы 5.6.1 и 5.6.2 касаются только независимости распределений и применимы независимо от того имеют квадратичные формы распределение c² или нет. Теорема о независимости нескольких квадратичных форм в этом смысле отличается от теорем 5.6.1 и 5.6.2. Она рассматривает статистическую независимость квадратичных форм в их сумме и описывает условия, при которых эти формы имеют нецентральные распределения c². По существу, она включает рассмотрение идемпотентных матриц. Эта теорема о распределении и независимости нескольких квадратичных форм. Её доказательство дано в [Searle (1971) стр. 61-64].

Теорема 5.6.3. Пусть вектор у имеет нормальное распределение N_п(y, S), а квадратичная форма у^TAy=(i =1, 2, ..., k), где матрица А= симметричная ранга r и все матрицы A_i симметричные размеров пхп и соответствующих рангов r_i. Тогда:

1. Квадратичные формы у^TA_iy имеют нецентральные распределения c²(r_i, y^TA_iy/2),

2. Квадратичные формы у^TA_iy попарно статистически независимы,

3. Квадратичная форма у^TAy имеет нецентральное распределение c²(r, y^TAy/2),

если и только если

I: любые два из следующих трех утверждений верны:

(a) Каждая матрица A_iS идемпотентная,

(b) Произведение A_iSA_j=O для всех i≠j (j =1, 2, ..., k),

(c) Матрица АS идемпотентная;

или

II: верны утверждения пунктов (с) и

(d) Ранг матрицы А равен сумме рангов матриц A_i, то есть, r=,

или

III: верны утверждения пунктов (с) и

(e) Матрицы A₁S, ..., A_(k-1)S идемпотентные и A_kS - неотрицательно определённая.

Доказательство этой теоремы из области статистики, но опирается на теорему о матрицах, которая, в свою очередь, основывается на лемме. Приведенная ниже теорема о матрицах является продолжением теорем, данных в [Graybill (1961) теоремы 1.68 и 1.69]. Приведённое здесь доказательство следует более короткому доказательству [Banerjee (1964)], улучшенному в [Loynes (1966)] и основанному на лемме. Поэтому сначала сформулируем лемму и приведём её доказательство.

Лемма 5.6. Если матрица В симметричная и идемпотентная, матрица Q симметричная и неотрицательно определенная и матрица I–B–Q неотрицательно определённая, то BQ=QB=О.

Доказательство: Пусть вектор а – любой соответствующих размеров, а вектор b=Ва. Тогда

b^TBb=b^TB²a=b^TBa=b^Tb

и поэтому

b^T(I–B–Q)b=b^Tb–b^TBb–b^TQb=–b^TQb.

Кроме того, поскольку матрица I–B–Q неотрицательно определенная, то

b^T(I–B–Q)b0.

Отсюда также –b^TQb0 и поэтому, так как Q тоже неотрицательно определенная, то b^TQb=0. Кроме того, поскольку Q является симметричной, то для некоторой матрицы L имеем Q=L^TL и, следовательно, b^TQbb^TL^TLb=0 означает Lb=0 и поэтому L^TLb=0, то есть, Qb=QBa=0. Поскольку это верно для любых значений вектора a, то QB=О и отсюда также

(QB)^T=B^TQ^T=BQ=О.

□

Далее рассмотрим теорему о матрицах.

Теорема 5.6.4. Пусть дано следующее:

Матрицы B_i размеров nxn симметричные и соответственно рангов k_i (i =1, 2, ..., p).

Матрица B= симметричная и ранга k.

Тогда, при следующих утверждениях:

(a) Матрицы B_i идемпотентные для всех i,

(b) Произведение B_iB_j=О при i ≠ j (j =1, 2, ..., p),

(c) Матрица B идемпотентная,

(d) k=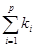

истинно то, что

I: из двух утверждений пунктов (а), (b) и (c) следует одно утверждение из пунктов (а), (b), (c) и (d);

II: из утверждений пунктов (с) и (d) следуют утверждения пунктов (а) и (b);

III: утверждение пункта (с) и то, что матрицы B₁, B₂, ..., B_p-1 идемпотентные, а матрица B_p неотрицательно определенная, значит, что B_p также идемпотентная и, следовательно, справедливо утверждение пункта (а), а поэтому справедливы и утверждения пунктов (b) и (d).

Обе теоремы 5.6.3 и 5.6.4 основаны на рассмотрении матриц. Если теорема 5.6.4 доказана, то доказательство теоремы 5.6.3 является относительно коротким. Роль теоремы 5.6.4 состоит в показе того, что в ситуациях, когда любой из разделов I, II или III теоремы 5.6.3 является верным, то все утверждения пунктов (а), (b) и (c) раздела I будут соблюдаться. Результаты теоремы 5.6.3, то есть независимость квадратичных форм и их распределений c², получаются непосредственно по теоремам 5.5 и 5.6.2.

Доказательство теоремы 5.6.4.

Приведём сначала доказательство раздела I, разделяя его на четыре части.

Раздел I часть 1: При справедливости утверждения пункта (с), т.е., матрица B идемпотентная, матрица I–B тоже идемпотентная и поэтому неотрицательно определённая. При данном утверждении пункта (а), т.е., матрицы B_i идемпотентные для всех i, матрица B–B_i–B_j = неотрицательно определенная. Поэтому сумма матриц I– B+B–B_i–B_j=I–B_i–B_j неотрицательно определенная и, следовательно, по лемме 5.6 получаем B_iB_j=О, что является утверждением пункта (b), т.е., произведение B_iB_j=О при i≠j. Следовательно, из утверждений пунктов (а) и (с) следует утверждение пункта (b).

Раздел I часть 2: Пусть l - собственное значение и u - соответствующий собственный вектор матрицы B_1. Тогда для l≠0 из уравнения B₁u=lu получаем u=B₁u/l. При справедливости утверждения пункта (b) для i≠1 получаем вектор B_iu=B_iB₁u/l равный 0. Следовательно, Bu=B₁u=lu и поэтому l - собственное значение матрицы B. Но, при справедливости утверждения пункта (с), матрица B идемпотентная и поэтому l равно 0 или 1. Следовательно, по теореме П.12.6 матрица B₁ идемпотентная. Точно так же другие матрицы B_i тоже идемпотентные и, таким образом, получено утверждение пункта (а). Следовательно, из утверждений пунктов (b) и (с) следует утверждение пункта (а).

Раздел I часть 3: При справедливости утверждений пунктов (а) и (b) имеем B²===B, что является утверждением пункта (с). Таким образом, из утверждений пунктов (а) и (b) следует утверждение пункта (с).

Раздел I часть 4: При справедливости утверждения пункта (с) имеем ранг(X)=след(X) и поэтому

k=ранг(B)=след(B)=след()=,

а при справедливости утверждения пункта (а), имеем =. Поэтому k =, что является утверждением пункта (d). Таким образом, из утверждений пунктов (а) и (с) следует утверждение пункта (d).

Раздел II: Доказательство этого раздела следует тому, что дано в [Loynes (1966)]. При справедливости утверждения пункта (с), т.е., что матрица B идемпотентная, матрица I–B является идемпотентной и поэтому B–I имеет ранг n–k, то есть B–I имеет n–k линейно независимых строк. Следовательно,

выражение (B–I)x=0 представляет n–k линейно независимых уравнений;

выражение B₂x=0 представляет k₂ линейно независимых уравнений;

....

выражение B_px=0 представляет k_p линейно независимых уравнений.

Тем не менее, эти наборы линейно независимых уравнений не все взаимно линейно независимы. Например, k₂ линейно независимых уравнений в B₂x=0 могут быть линейно зависимы от k_p линейно независимых уравнений в B_px=0. Таким образом, в

=0

максимальное число линейно независимых уравнений, при справедливости утверждения пункта (d), находится из выражения

n–k+k₂+…+k_p=n–k₁

и уравнения сводятся к B₁x=x. Таким образом, минимальное число линейно независимых решений для B₁x=x равно n–(n–k₁)=k₁, то есть, по меньшей мере, k₁ линейно независимых векторов х и уравнение собственных значений-векторов имеет вид B₁x=x=lx. Таким образом l – собственное значение матрицы B₁ кратности равной, по меньшей мере, k_1. Но ранг(B₁)=k₁ и B₁ имеет только k₁ ненулевых собственных значений, поэтому по теореме П.12.6 является идемпотентной. Точно так же и другие матрицы B_i и, следовательно, получается утверждение пункта (а). Таким образом, из утверждений пунктов (с) и (d) следует утверждение пункта (а) и, как доказано в части 1 раздела I, следует также утверждение пункта (b) и этим раздел II доказан.

Раздел III: При справедливости утверждения пункта (с), матрица B неотрицательно определённая и тогда также матрица I–B. При идемпотентных матрицах B₁, ..., B_p-1, и, поэтому, положительно определённых, матрица B_p также неотрицательно определённая. Тогда матрица =B–B_i–B_j является неотрицательно определённой. Поэтому матрица I–B+B–B_i–B_j=I–B_i–B_j является неотрицательно определённой и, следовательно, по лемме 5.6 имеем B_iB_j=О, то есть, утверждение пункта (b) верно. Таким же образом получаются утверждения пунктов (а) и (d) и этот раздел, а также вся теорема доказаны.

□

Теперь с использованием теоремы 5.6.4 докажем теорему 5.6.3.

Доказательство теоремы 5.6.3.

Так как матрица S симметричная и положительно определённая, то по теореме П.6.3 она может быть представлена в виде S=T^TT, где T некоторая невырожденная матрица. Тогда, поскольку A_i симметричная, то также и матрица TA_iT^T, а ранг(A_i)=ранг(TA_iT^T). Матрица A_iS идемпотентная, если и только если TA_iT^T идемпотентная, и A_iSA_j=О, если и только если TA_iT^TTA_jT^T=O. Таким образом, теорема 5.6.4 остаётся в силе и при использовании TA_iT^T вместо B_i (и TAT^T вместо B). Тогда разделы I, II и III теоремы 5.6.4 применяемые к TA_iT^T и TAT^T показывают, что когда разделы I, II или III теоремы 5.6.3 имеют место, то утверждения пунктов (а), (b) и (с) всегда имеют место. Но, по теореме 5.5 квадратичная форма у^TA_iу имеет нецентральное распределение c²(k_i, y^TA_iy/2), если и только если утверждение пункта (а) верно. Кроме того, квадратичная форма y^TAy имеет нецентральное распределение c²(k, y^TAy/2), если и только если утверждение пункта (c) верно. А по теореме 5.6.2 квадратичные формы y^TA_iy и y^TA_jy статистически независимы, если и только если утверждение пункта (b) верно. Этим теорема 5.6.3 доказана.

□

Теорема 5.6.3 описывает разделение суммы квадратов на несколько составляющих сумм квадратов. Следующее её следствие рассматривает частный случай, где А=I, то есть случай разделения общей суммы квадратов y^Ty на несколько сумм квадратов.

Следствие 1. Пусть у ~ N_п(y, s²I), матрицы A_i (i =1, 2, ..., k) симметричные рангов r_i и y^Ty=. Тогда квадратичные формы у^TA_iy/s² имеет соответственно нецентральные распределения c²[r_i, y^TA_iy/(2s²)] и взаимно независимы, если и только если выполняется любое из следующих условий:

Ø Каждая матрица A_i идемпотентная.

Ø Произведение A_iA_j=O для всех i≠j (j=1, 2, ..., k).

Ø n=.

□

Это следствие 1 теоремы 5.6.3 было доказано в статье [Cochran (1934)].

Упражнения

5.1. Получите выражение для D(s²) указанными ниже способами (а) и (б), считая, что у^T=[y₁, y₂, ..., у_n] имеет распределение N_n(y1, s²I) и s² вычисляется по формуле s²=.

(а) Выразить s² в виде s²=y^Т(I–E/n)y/(n–1) и воспользоваться теоремой 5.2.3.

(б) Учесть, что переменная u =(n–1)s²/s² имеет распределение c²(n–1) и поэтому D(u)=2(n–1). Тогда D(s²)=D[s²u/(n–1)].

5.2. Покажите, что у^TAy–y^TAy=(y–y)^TA(y–y)+2(y–y)^TAy, как в (5.2.9).

5.3.      (а) Покажите, что  в (5.2.12) равна  в (5.2.13).

(б) Покажите, что =x^T(I–Е/n)y, как в (5.2.13) в примере 5.2.2.

5.4. Если переменная v имеет распределение c²(n, g), то пользуясь теоремой 5.2.3 покажите, что D(v)=2n+8g, как в (5.3.7).

5.5. Если v имеет распределение c²(n, g), то используйте функцию производящую моменты по формуле (5.3.8) чтобы найти E(v) и D(v). [Совет: Используйте ln[M_v(t)], затем d{ln[M_v(0)]}/dt =E(v) и d²{ln[M_v(0)]}/dt²=D(v). Запись d{ln[M_v(0)]}/dt означает, что d{ln[M_v(t)]}/dt оценивается при t=0, обозначение d²{ln[M_v(0)]}/dt² определяется аналогично.]

5.6. Если вектор у ~ N_n(y, S), то, используя теорему 5.5, проверьте, что квадратичная форма (у–y)^Т S^–1(у–y) имеет распределение c²(n), как в (5.3.8). Какое распределение имеет квадратичная форма у^ТS^–1у?

5.7. Докажите следующие дополнительные следствия теоремы 5.5:

1. Если у ~N_p(y, s²S), то у^TAy/s² имеет распределение c²[r, y^TAy/(2s²)], если и только если AS идемпотентная и ранга r.
2. Если у ~N_p(y, s²S), то отношение у^ТS^–1у/s² ~ c²[р, y^TS^–1y/(2s²)].

5.8. Покажите, что 1^T(I–Е/n)=0^T, как в примере 5.6.2.

5.9. Пусть y₁, y₂, ..., у_n - случайная выборка из популяции с распределением N(y, s²), так что у^Т= [y₁, y₂, ..., у_n] имеет распределение N_n(y1, s²I). В примере 5.5 показано, что (n–1)s²/s²= имеет распределение c²(n–1). В примере 5.6.2 показано, что  и s²= статистически независимы.

1. Покажите, что  имеет распределение N(y, s²/n).
2. Покажите, что t_у=(–y)/() имеет распределение t(n–1).
3. При условии y₀≠y, покажите, что t₀=(–y₀)/() имеет распределение t(n–1, d). Найдите d.

5.10. Положим, что у ~ N_n(y1, s²I). Найдите распределение статистики

u=.

(Эта статистика может быть использована для проверки гипотезы H₀: y=0)

5.11. Пусть у ~ N_p(y, S), где y=y1 и

S=s².

Таким образом, E(y_i)=y и D(y_i) =s² для всех i и C(y_i, y_j)=s²r для всех i ≠j, то есть переменные y_i являются одинаково коррелированными.

1. Покажите, что S можно записать в виде S=s²[(1–r)I+rЕ].
2. Покажите, что  имеет распределение c²(n–1).

5.12. Положим, что у ~ N₃(y, S), где

y=,        S=.

Пусть

A=.

1. Найдите E(у^TAy).

2. Найдите D(у^TAy).

3. Имеет ли у^TAy распределение c²?

4. Если S=s²I, то имеет ли у^TAy/s² распределение c²?

5.13. Полагая, что у ~ N₃(y, S), где

y= и S=.

Найдите симметричную матрицу А такую, что у^TAy имеет распределение c²(3, y^TAy/2). Что такое y^TAy/2?

5.14. Полагая, что у ~ N₄(y, S), где

y= и S=,

найдите матрицу А такую, что у^TAy имеет распределение c²(4, y^TAy/2). Что такое y^TAy/2?

5.15. Допустим, что у ~ N₃(y, s²I) и пусть

y=, A=, В=.

1. Какое распределение имеет у^TAy/s²?

"1 часть" - тут тоже много полезного для Вас.

2. Являются ли у^TAy и Ву независимыми?

3. Являются ли у^TAy и y₁+y₂+y₃ независимыми?

5.16. Положим, что у ~ N₃(y, s²I), где y^T= [1, 2, 3], и пусть

B=.

1. Какое распределение имеет у^TВy/s²?
2. Является ли у^TВy зависимой от у^TAy, где А из упражнения 5.15?

5.17. Положим, что у ~ N_n(y,s²I) и X - матрица числовых значений размеров nхp и ранга р<n.

1. Покажите, что H=X(X^TX)^–1X^T и I–H=I–X(X^TX)^–1X^T идемпотентные и найдите ранги этих матриц.
2. Полагая, что y является линейной комбинацией столбцов X, то есть y=Xb для некоторого b [см. (П.3.3)], найдите E(у^THy) и E[у^T(I–H)y], где H такая, как определено в пункте 1.
3. Найдите распределения величин у^THy/s² и у^T(I–H)y/s².
4. Покажите, что у^THy и у^T(I–H)y независимы.
5. Найдите распределение отношения

.