Производящие моменты функции

4.4. Производящие моменты функции

Результаты раздела 4.1 можно использовать для нахождения функции, производящей моменты нормального распределения вектора случайных переменных. Во-первых, если вектор z имеет стандартное многомерное нормальное распределение N_n(0, I_n), то, благодаря независимости переменных z₁, z₂, …, z_n, производящая моменты распределения вектора z функция имеет вид

E[ехр(t^Тz)]=E[ехр]

=E[]

=

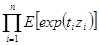
= [в силу (4.1.2)]

=exp(t^Tt/2).                                                    (4.4.1)

Теперь, если вектор y имеет нормальное распределение N_n(y, S), то, как показано выше, преобразование вектора z в вектор у записывается в виде у=S^1/2z+y. Следовательно, используя (4.4.1) и полагая s=S^1/2t, функция M_у(t)=E[ехр(t^Ty)], производящая моменты распределения вектора у, приобретает вид

E[ехр(t^Ty)] =E[ехр{t^T(S^1/2z+y)}]

Рекомендуемые материалы

=E[ехр(s^Tz)]ехр(t^Ty)

=ехр(s^Ts/2)ехр(t^Ty)                  [в силу (4.4.1)]

=ехр(t^TS^1/2S^1/2t/2+t^Ty)

=ехр(t^Ty+t^TSt/2).                                          (4.4.2)

Кроме этого, функция, производящая моменты распределения разности векторов у–y, имеет вид

M_у–y(t)=E[ехр{t^T(у–y)}]

=ехр(–t^Ty)E[ехр(t^Tу)]

=ехр(–t^Ty)ехр(t^Ty+t^TSt/2)

=ехр(t^TSt/2).                                                  (4.4.3)

Другой хорошо известный факт об одной нормально распределенной переменной состоит в том, что если у~N(y, s²), то её линейная функция ay+b имеет распределение в виде N(аy+b, а²s²), при условии a≠0. Аналогичный результат верен и для нормально распределенного вектора случайных переменных, что доказывается в следующей теореме [Seber, Lee (2003) стр.20].

Теорема 4.4.1. Пусть вектор y случайных переменных имеет нормальное распределение N_n(y, S), а матрица С размеров mхп и ранга т и вектор d размеров mх1 состоят из некоторых числовых значений, тогда вектор Cy+d имеет нормальное распределение N_m(Cy+d, CSC^T).

Доказательство: Функцией, производящей моменты распределения вектора Cy+d, является

E[ехр{t^T(Cy+d)}]=E[ехр{(C^Tt)^Ty+t^Td}]

=ехр[(C^Tt)^Ty+(C^Tt)^TSC^Tt/2+t^Td]     [по (4.4.2)]

=ехр[t^T(Cy+d)+t^TCSC^Tt/2].

Так как матрица CSC^T положительно определенная, то это выражение является функцией, производящей моменты распределения вектора Cy+d, имеющего распределение N_m(Cy+d, CSC^T). А так как многомерное нормальное распределение было определено только для положительно определенных дисперсионных матриц, то матрица C должна иметь полный ранг, чтобы матрица CSC^T была положительно определенной. Это подтверждается тем, что, например, для векторов а и b=C^Tа имеем а^TCSC^Tа=b^TSb≥0 при равенстве, если и только если b=0, C^Tа=0 и а=0 (так как столбцы матрицы C^T линейно независимы). Таким образом а^TCSC^Tа>0 для всех а≠0.

□

Следствие. Если у=Аz+y, где А - невырожденная матрица размеров пхп, то вектор y имеет нормальное распределение N_n(y, АА^T).

Доказательство: Функцией, производящей моменты распределения вектора Аz+y, является

E[ехр{t^T(Аz+y)}]=E[ехр{(А^Tt)^Tz+t^Ty}]

=ехр[(А^Tt)^TI_nА^Tt/2+t^Ty]       [по (4.4.2)]

=ехр[t^Ty+t^TАА^Tt/2].

Так как матрица АI_nА^T положительно определенная по тем же соображениям, что указаны в теореме, то полученное выражение является функцией, производящей моменты распределения вектора Аz+y~N_п(y, АА^T).

□

Пример 4.4.1. Предположим, что z~N_n(0, I_n) и M - ортогональная матрица. Тогда, по теореме 4.4.1 вектор х=M^Tz распределён также в виде N_n(0, I_n), так как M^TM=I_n.

□

Если вектор у случайных переменных размеров пх1 и вектор t некоторых числовых значений размеров пх1, то функция, производящая моменты распределения вектора у, определяется в виде

M_у(t)=E[ехр(t^Ту)]=E[ехр(t₁у₁+t₂у₂+...+t_nу_n)]

=E[ехр(t₁у₁)ехр(t₂у₂)...ехр(t_nу_n)].

Основным свойством производящей моменты функции является то, что, если M_у(t) существует для всех норм вектора ||t||≤t₀ (t₀>0) (то есть в области, содержащей начало отсчёта), то она однозначно определяет распределение вектора у [Seber, Lee (2003) стр.13]. К счастью, большинство обычных распределений имеют производящие их моменты функции. Одним исключением является распределение t (с некоторыми из своих моментов бесконечными, включая распределение Коши с 1 степенью свободы). Приведём пример, где эта уникальность применяется с пользой. Полагаем, что читатель знаком с функцией, производящей моменты распределения c²(r), а именно (1–2t)^–r/2.

Пример 4.4.2. Пусть переменные q₁~c²(r₁), q₂~c²(r₂) и переменная q=q₁–q₂ статистически независима от q₂. Теперь покажем, что q~c²(r), где r=r₁–r₂. Записывая

(1–2t)^–r1/2=E[ехр(tq₁)]

=E[ехр(tq+tq₂)]

=E[ехр(tq)]E[ехр(tq₂)]

=E[ехр(tq)](1–2t)^–r2/2,

имеем

E[ехр(tq)]=(1–2t)^{–(r1–r2)/2},

что является функцией, производящей моменты распределения c²(r).

□

Производящие моменты функции дают также удобный метод доказательства статистической независимости. Например, если существует функция M_у(t), производящая моменты распределения вектора у случайных переменных, и она разлагается на множители в виде

M_у(t) =M_у1(t₁, ..., t_r, 0, ..., 0)M_у2(0, ..., 0, t_r+1, ..., t_n),

то подвекторы у₁^T=[у₁, у₂, …, у_r] и у₂^T=[у_r+1, у_r+2, …, у_n] вектора у статистически независимы. Справедливым является также и то, что у₁ и у₂ независимы, если и только если для некоторых функций этих векторов их совместная производящая моменты функция раскладывается на множители, являющиеся функциями, производящими моменты распределений этих векторов.

Пример 4.4.3. Положим, что совместное распределение векторов х и у случайных переменных имеет совместную производящую моменты функцию, которая существует в области изменения вектора t, содержащей начало отсчёта. Тогда, если независимы векторы х и у, то независимы и любые (измеримые) функции от них. Это следует из того, что, если с(х) и d(у) соответствующие вектор-функции, то

E[ехр{t^Tc(х)+t^Td(у)}]=E[ехр{t^Tc(х)}]E[ехр{t^Td(у)}].

Этот результат, по сути, верен для любых векторов х и у, даже если не существует их производящих моменты функций, что можно доказать, используя характеристические функции [Seber, Lee (2003) стр.14].

□

Другой способ доказательства независимости основан на рассмотрении ковариации. Хорошо известно, что, в общем случае, С(х, у)=0 не означает независимость переменные х и у. Тем не менее, в важном случае двумерного нормального распределения переменных х и у они независимы, если и только если С(х, у)=0. Для большего числа переменных в многомерных нормальных распределениях переменные независимы друг от друга, если и только если они попарно независимы. Однако попарная независимость ещё не означает совместную независимость. Это показано в следующем примере.

Пример 4.4.4. Положим, что x₁, x₂ и x₃ имеют функцию совместной плотности

f(x₁, x₂, x₃)= (2p)^–3/2ехр[–(x₁+x₂+x₃)/2]{1+x₁x₂x₃ехр[–(x₁+x₂+x₃)/2]}

–∞<x_i<∞         (i =1, 2, 3).

Тогда второе слагаемое в фигурных скобках этого выражения - нечетная функция x₃, так что при –∞<x₃<∞ её интеграл равен нулю. Следовательно

f₁₂(x₁, x₂)=(2p)^–1ехр[–(x₁²+x₂²)/2]

=f₁(x₁)f₂(x₂),

и x₁ и x₂ являются независимыми переменными, распределёнными в виде N(0, 1). Таким образом, хотя x₁, x₂ и x₃ попарно независимы, они не являются совместно независимыми, так как получается неравенство

Информация в лекции "11.3 Основные направления внешней политики" поможет Вам.

f(x₁, x₂, x₃)≠(2p)^–3/2ехр[–(x₁²+x₂²+x₃²)/2]=f₁(x₁)f₂(x₂)f₃(x₃).

□

В итоге отметим два важных свойства производящих моменты функций.

1. Если два вектора случайных переменных имеют одинаковую функцию, производящую моменты их распределений, то они имеют одинаковую функцию плотности вероятности.

2. Два вектора случайных переменных независимы, если и только если их совместная производящая моменты функция представляется произведением их двух отдельных производящих моменты функций, то есть, если y^Т=[y₁^Т, y₂^Т] и t^Т=[t₁^Т, t₂^Т], то y₁ и y₂ независимы, если и только если

М_у(t)=М_у1(t₁)М_у2(t₂).                                                  (4.4.4)