Свойства многомерного нормального распределения

4.5. Свойства многомерного нормального распределения

Определение многомерного нормального распределения

Пусть вектор z имеет стандартное многомерное нормальное распределение N_n(0, I_n), а матрица А размеров пхт и вектор y размеров пх1 состоят из некоторых чисел. При замене матрицы S^1/2 на А в выводе выражения (4.4.2) видно, что функцией, производящей моменты распределения вектора у=Аz+y, является ехр(t^Ty+t^TSt/2), где S=АА^T. Распределения векторов одинаковы, если они имеют одну и ту же функцию, производящую моменты их распределений. Следовательно по этой функции распределение вектора у зависит только от A через матрицу АА^T. Заметим также, что E(у)=АE(z)+y=y и С(y)=AС(z)A^T=АА^T. Эти доводы обосновывают введение нового определения многомерного нормального распределения.

Определение 4.2. Случайный вектор у размеров пх1, имеющий вектор средних y и дисперсионную матрицу S, имеет многомерное нормальное распределение, если он имеет такое же распределение, как вектор Аz+y, где матрица А размеров пхт удовлетворяет равенству АА^T=S и вектор z~N_n(0, I_т). Обозначение у~Аz+y показывает, что векторы у и Аz+y имеют одинаковое распределение.

Докажем, что если матрица S положительно определенная, то новое определение эквивалентно старому определению 4.1. Как показано выражениями (4.3.7), распределение инвариантно к виду матрицы А до тех пор пока АА^T=S. Если матрица S имеет полный ранг (или, что то же самое, положительно определенная), то существует невырожденная матрица А такая, что S=АА^T. Если по определению 4.1 вектор у имеет многомерное нормальное распределение, то по теореме 4.4.1 вектор z=А^–1(y–y) имеет распределение N_n(0, I_т), так что y имеет многомерное нормальное распределение в смысле определения 4.2. И наоборот, если y по определению 4.2 имеет многомерное нормальное распределение, то функция, производящая моменты его распределения, дается формулой (4.4.2). Но она также и функция, производящая моменты распределения случайного вектора, имеющего функцию плотности (4.2.7), так что, ввиду единственности производящей моменты функции, распределение вектора у также имеет функцию (4.2.7) плотности вероятности.

Если матрица S имеет ранг т<п, то распределение вектора у не может быть выражено через функцию плотности вероятности. В обоих случаях, независимо от того, является ли S положительно или неотрицательно определенной, выше было показано, что для вектора у функцией, производящей моменты его распределения, является

М_у(t)=ехр(t^Ty+t^TSt/2).                                             (4.5.1)

Как и ранее, в случае невырожденной матрицы S пишем y~N_т(y, S). Когда матрица S имеет ранг меньше полного, то иногда говорят, что вектор у имеет сингулярное или вырожденное распределение. Далее не будет делаться допущения, что S положительно определенная, если это явно не указано.

Пример 4.5.1. Пусть y~N_т(y, S) и положим y^T= [y, –y]. Ковариационной матрицей распределения вектора y является

Рекомендуемые материалы

S=s².

Положим z=(y–y)/s. Тогда

y= z+=az+y

и

S=aa^T.

Таким образом, y имеет многомерное нормальное распределение.

□

Пример 4.5.2. Можно показать, что теорема 4.4.1 остается верной и для векторов случайных переменных, имеющих многомерные нормальные распределения по приведённому выше расширенному определению без ограничения на ранг матрицы А. Если y~N_п(y, S), то у~Аz+y. Следовательно, Cу~CАz+Cy=Вz+b и вектор Cу имеет многомерное нормальное распределение с Е(Cу)=b=Cy и С(Cу)=ВВ^T=CАА^TC^T=CSC^T.

□

Пример 4.5.3. В рамках расширенного определения, вектор некоторых числовых значений имеет многомерное нормальное распределение. (Возьмём матрицу О из нулей.) В частности, если 0_с - нулевой вектор строка, то при этом определении скалярная постоянная имеет (одномерное) нормальное распределение, так что числовые величины можно рассматривать как нормально распределённые (с нулевой дисперсией).

□

В итоге описание многомерного нормального распределения формулируется следующей теоремой.

Теорема 4.5.1. Вектор у случайных переменных с ковариационной матрицей S и вектором средних y имеет нормальное распределение N_п(y, S), если и только если переменная а^Tу имеет одномерное нормальное распределение для любых числовых элементов вектора а.

Доказательство: Сначала предположим, что y~N_п(y, S). Тогда у~Аz+y, так что а^Tу~а^TАz+а^Ty=(А^Tа)^Tz+а^Ty. Переменная а^Tу имеет (одномерное) нормальное распределение в смысле определения 4.2.

Обратно, допустим, что t^Tу является одномерной нормальной случайной переменной для любых числовых элементов вектора t. Она имеет среднее значение t^Ty и дисперсию t^TSt. Используя формулу (4.1.6) функции, производящей моменты нормального распределения одной переменной, находим

E[ехр{t_l(t^Tу)}]=ехр[t_l(t^Ty)+t_l²(t^TSt)/2].

Принимая t_l=1, получаем, что функция, производящая моменты распределения вектора у, задается выражением (4.5.1) и, таким образом, y~N_п(y, S).

□

Распределения линейных функций нормального вектора

Рассмотрим распределения линейных функций векторов случайных переменных, распределённых по нормальному закону.

Теорема 4.5.2. Пусть вектор y случайных переменных размеров nх1 имеет нормальное распределение N_n(y, S), а - любой вектор числовых значений размеров nх1 и А - любая матрица числовых значений размеров kхn и ранга k≤n. Тогда,

1. Переменная х=a^Ty имеет нормальное распределение N(a^Ty, a^TSa).
2. Вектор х=Ау имеет нормальное распределение N_k(Ay, ASA^T).

Доказательство:

1. Функция, производящая моменты распределения переменной х=a^Ty, задается в виде

М_х(t) =E[exp(tх)]=E[exp(ta^Ty)]=E[exp{(ta)^Ty}]

=E[exp{(ta)^Ty+(ta)^TS(ta)/2}]  [в силу (4.5.1)]

=exp[(a^Ty)t+(a^TSa)t²/2}.                                           (4.5.2)

Из сравнения выражений (4.5.2) и (4.1.6) ясно, что переменная х=a^Ty является одномерной нормально распределённой со средним a^Ty и дисперсией a^TSa.

1. Функция, производящая моменты распределения вектора x=Ay, задается выражением

М_x(t)=E[exp(t^Tx)]=E[exp(t^TAy)].

Так как E[exp(t^TAy)]=E{exp[(A^Tt)^Ty]}, то, используя (4.4.2) с вектором A^Tt вместо t, получаем

М_x(t)=exp[t^T(Ay)+t^T(ASA^T)t/2].                              (4.5.3)

По следствию 1 теоремы П.6.2, матрица ковариаций ASA^T положительно определённая. Таким образом, в силу (4.4.2) и (4.5.3), вектор x=Ay случайных переменных размеров kx1 распределён в виде N_k(Ay, ASA^T).

□

Следствие 1. Если b - любой вектор некоторых числовых значений размеров kх1, то вектор х=Ay+b имеет нормальное распределение N_k(Ay+b, ASA^T).

Доказательство: Функция, производящая моменты распределения вектора x=Ay+b, задается выражением

М_x(t)=E[exp(t^Tx)]=E{exp[t^T(Ay+b)]}=exp(t^Tb)E[exp(t^TAy)]

=exp(t^Tb)exp[t^T(Ay)+t^T(ASA^T)t/2]                          [в силу (4.5.3)]

=exp[t^T(Ay+b)+t^T(ASA^T)t/2],

которая является функцией, производящей моменты нормального распределения вектора х с вектором средних Ay+b и ковариационной матрицей ASA^T.

□

Распределения подвекторов нормального вектора

Подвекторы вектора случайных переменных, распределённых по нормальному закону, также распределены по нормальному закону. Это доказывается в следующей теореме.

Теорема 4.5.3. Если вектор у имеет нормальное распределение N_n(y, S), то любой его подвектор размеров rх1 имеет нормальное распределение соответственно c теми же средними, дисперсиями и ковариациями как в исходном нормальном распределении N_n(y, S).

Доказательство: Без ограничения общности, пусть вектор у разделён следующим образом y^T=[y₁^T, y₂^T], где y₁ - любой подвектор размеров rх1. Пусть соответствующим образом разделены вектор y и матрица S:

у=, y= и S=.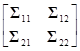

Обозначим разделённую матрицу А=[I_r, O], где I_r - единичная матрица размеров rхr и O - матрица нулей размеров rх(п–r). Тогда Ау=y₁ и по пункту 2 теоремы 4.5.2 вектор y₁ имеет нормальное распределение N_r(y₁, S₁₁).

□

Следствие 1. Если вектор y имеет нормальное распределение N_п(y, S), то любая переменная у_i вектора у имеет нормальное распределение N(y_i, s_ii).

□

Пример 4.5.4. (Безусловные распределения) Положим, что y~N_п(y, S) и векторы y, y и матрица S разделены, как показано в доказательстве теоремы 4.5.3. Тогда y₁~N_р(y₁, S₁₁). Это видно из записи y₁=Bу, где матрица B=[I_р, 0]. Тогда By=y₁ и ВSВ^T=S₁₁, поэтому результат следует из теоремы 4.4.1. Очевидно, что элементами подвектора y₁ может быть любое подмножество элементов вектора y. Другими словами, безусловные распределения многомерного нормального вектора являются многомерными нормальными.

□

В примере 4.5.4 показано, что многомерное нормальное распределение имеет безусловные нормальные и, в частности, его одномерные безусловные распределения являются нормальными. Тем не менее, обратное утверждение неверно. Это видно из следующего примера. Рассмотрим функцию

f(y₁, у₂) =(2p)^–1exp[–(y₁²+у₂²)/2]{1+y₁y₂exp[–(y₁²–y₂²)/2]},

являющуюся неотрицательной, так как 1+уexp(–y²)>0, и её интеграл равен 1, так как интеграл exp(–y²/2)dy=0. Таким образом, f(y₁, у₂) представляет собой функцию совместной плотности вероятности, но это не функция плотности вероятности двумерного нормального распределения. Тем не менее,

=exp(–y₁²/2)

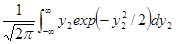
+y₁exp(–y₁²/2)

=exp(–y₁²/2),

так что безусловными распределениями являются N(0, 1). Пользуясь теоремой 4.5.1 для доказательства, что у имеет двумерное нормальное распределение, необходимо показать, что a^Tу имеет нормальное распределение для любых векторов а, а не только для векторов [1, 0] и [0, 1]. Известны многие другие примеры, такие как этот; смотрите, например, [Pierce, Dykstra (1969), Joshi (1970) и Kowalski (1970)].

Независимость подвекторов нормального вектора

В следующих двух теоремах будут использоваться обозначения из доказательства теоремы 4.5.3, где вектор у случайных переменных разделён на два подвектора у₁ размеров рх1 и у₂ размеров qх1 при соответствующем разделении вектора y и матрицы S.

В силу (3.2.13), если две случайные переменные у₁ и у₂ независимы, то s₁₂=0. Обратное для этого, в общем, неверно. В более широком смысле, если два вектора у и х случайных переменных статистически независимы (то есть, каждая переменная вектора у не зависит от каждой переменной вектора х), то S_yx=O (ковариации каждой переменной вектора у с каждой переменной вектора х равны 0). Обратное, в общем, тоже неверно, но для подвекторов у₁ и у₂ случайных переменных вектора у, распределённых совместно по нормальному закону с матрицей ковариаций S₁₂=O, обратное утверждение тоже верно.

Теорема 4.5.4. Если вектор у= имеет распределение по нормальному закону N_р+q(y, S), то его подвекторы у₁ и у₂ статистически независимы, если S₁₂=O.

Доказательство: Положим S₁₂=O. Тогда дисперсионная матрица

S=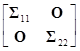

и показатель производящей моменты функции в выражении (4.4.2) принимает вид

t^Tm+t^TSt/2=[t₁^T, t₂^T]+[t₁^T, t₂^T]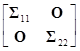/2

=t₁^Ty₁+t₂^Ty₂+t₁^TS₁₁t₁/2+t₂^TS₂₂t₂/2.                           (4.5.4)

Производящая моменты функция записывается так

M_v(t) =exp(t₁^Ty₁+t₁^TS₁₁t₁/2)exp(t₂^Ty₂+t₂^TS₂₂t₂/2),

что является произведением функций, производящих моменты распределений векторов у₁ и у₂. Следовательно, в силу (4.4.3), подвекторы у₁ и у₂ статистически независимы.

□

Следствие 1. Если вектор у распределён в виде N_п(y, S), то в нём любые две отдельные переменные у_i и у_j независимы, если их ковариация s_ij=0.

□

Условие независимости линейных функций случайного вектора приводится в следующем следствии.

Следствие 2. Если вектор у~N_п(y, S) и С(Ay, By)=ASB^T=O, где A и В - матрицы некоторых числовых значений, то случайные векторы u=Ay и v=By независимы.

Доказательство: Рассмотрим

w==y.

Тогда, по теореме 4.4.1 вектор w случайных переменных имеет многомерное нормальное распределение с ковариационной матрицей

С(w)=С(y)[A^T, B^T]=.

Таким образом, по теореме 4.5.4 векторы u и v независимы, если и только если ASB^T=О.

□

Пример 4.5.5. Пусть y~N_п(y, s²I_n) и 1_n - вектор единиц. Тогда выборочное усреднённое =n^–1не зависит от выборочной дисперсии s²= (п–1)^–1. Чтобы в этом убедиться, пусть Е_пn=1_n1_n^T - матрица единиц. Тогда =n^–11_n^Ty (=Ау) и

= (I_п–n^–1Е_пn)y=By.

Найдём

ASB^T=n^–11_n^Ts²I_n(I_п–n^–1Е_пn)= s²n^–11_n^TI_n–s²n^–1n^–11_n^T1_n1_n^T=s²n^–11_n^T–s²n^–11_n^T=0^T,

поэтому по теореме 4.5.4  не зависит от  и, следовательно, не зависит от s².

□

Пример 4.5.6. Для примера применения теорем 4.5.2 - 4.5.4 положим, что у~N₃(y, S), где

y= и S=.

Для переменной х=y₁–2у₂+у₃=[1, –2, 1]у=a^Ty имеем a^Ty=3 и a^TSa=19. Отсюда по пункту 1 теоремы 4.5.2 переменная х имеет распределение N(3, 19).

Линейные функции

x₁=y₁–у₂+у₃ и x₂=–3y₁+у₂–2у₃

можно записать совместно в виде

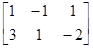
x===Ау.

Тогда по пункту 1 теоремы 3.6.2 и пункту 1 теоремы 3.6.4 получаем

Ay= и ASA^T=,

а по пункту 2 теоремы 4.5.2 имеем x с распределением в виде N₂.

Применяя теорему 4.5.3, получаем, что y₁ имеет распределение N(3, 4), у₃ имеет распределение N(2, 3), вектор  имеет распределение N₂ и вектор  имеет распределение N₂.

По теореме 4.5.4 заметим, что s₁₂=0 и, следовательно, y₁ и y₂ независимы.

□

Условное распределение подвектора нормального вектора

Пусть у= - разделённый вектор случайных переменных размеров (q+р)х1 и случайные переменные подвектора у₂ размеров рх1 имеют значения, представленные вектором у₂. Положим, вектор у имеет распределение по нормальному закону N_q+р(y, S), а вектор средних y и ковариационная матрица S разделены соответственно в виде

y= и S=.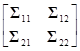

Тогда условное многомерное нормальное распределение вектора у₁ дается в следующей теореме.

Теорема 4.5.5. Если матрица S₂₂ положительно определённая, то распределение вектора у₁, при данном у₂=y₂, является условным многомерным нормальным у₁|(у₂=y₂)~N[E(у₁|у₂), С(у₁|у₂)] со следующими вектором средних и матрицей ковариаций

E(у₁|у₂)=y₁+S₁₂S₂₂^–1(у₂–y₂),                                    (4.5.5)

С(у₁|у₂)=S₁₁–S₁₂S₂₂^–1S₂₁.                                          (4.5.6)

Доказательство: [Boik (2011) стр.140] Пусть В - матрица размеров qхp некоторых числовых значений. Рассмотрим ковариацию С(у₁–Ву₂, у₂) двух векторов у₁–Ву₂ и у₂. Она представляется в виде:

С(у₁–Ву₂, у₂)=С{[I_q, –В]у, [O_pq, I_p]у},

так как у=, у₁–Ву₂=[I_q, –В]у и у₂=[O_pq, I_p]у. По пункту 2 теоремы 3.6.4

С{[I_q, –В]у, [O_pq, I_p]у}=[I_q, –В]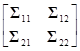

=S₁₂–ВS₂₂.

Допустим матрица S₂₂ положительно определённая и выберем матрицу В такой, чтобы С(у₁–Ву₂, у₂)=O. Отсюда получаем ВS₂₂=S₁₂ и В=S₁₂S₂₂^–1.

По пункту 2 теоремы 4.5.2 совместное распределение представляемых произведением

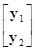
векторов у₁–Ву₂=у₁–S₁₂S₂₂^–1у₂ и у₂, имеет вид

~N(y*, S*),

где

y*==

и

S*=

=.

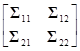
По теореме 4.5.4 следует, что векторы у₁–S₁₂S₂₂^–1у₂ и у₂ статистически независимы. При независимости условное распределение вектора у₁–S₁₂S₂₂^–1у₂, при у₂=y₂, имеет вид

у₁–S₁₂S₂₂^–1у₂|(у₂=y₂)~N(y₁–S₁₂S₂₂^–1y₂, S₁₁–S₁₂S₂₂^–1S₂₁)

и условное распределение вектора у₁–S₁₂S₂₂^–1у₂+S₁₂S₂₂^–1у₂=у₁, при у₂=y₂, имеет вид

у₁|(у₂=y₂) ~N(y₁–S₁₂S₂₂^–1y₂+S₁₂S₂₂^–1у₂, S₁₁–S₁₂S₂₂^–1S₂₁)

или

у₁|(у₂=y₂) ~N[y₁+S₁₂S₂₂^–1(у₂–y₂), S₁₁–S₁₂S₂₂^–1S₂₁].

□

Используя формулу (1.7.1), функция условной плотности вероятности вектора у₁ при данном y₂ следующая

f(у₁|у₂)=g(у)/h(у₂),                                          (4.5.7)

где g(у) - совместная функция плотности вероятности векторов у₁ и у₂, а h(у₂) - функция плотности вероятности безусловного распределения вектора у₂. Доказательство теоремы 4.5.5 может быть выполнено путем непосредственного вычисления отношения в правой части выражения (4.5.7) [Rencher, Schaalje (2008) стр. 95].

Поскольку в (4.5.5) E(у₁|у₂)=y₁+S₁₂S₂₂^–1(у₂–y₂) является линейной функцией у₂, то любая пара разных переменных у_i и у_j в нормально распределённом векторе у проявляет линейную тенденцию E(у_i|у_j) =y_i+(s_ij/ s_jj)(у_j–y_j). Таким образом, ковариация s_ij связана с наклоном линии, представляющей тенденцию, и s_ij является полезной мерой взаимосвязи между двумя переменными, распределёнными по нормальному закону. В случае если переменные распределены по другому закону и проявляют тенденцию отличную от линейной, то s_ij может дать очень искаженное представление их взаимосвязи.

Матрица условных ковариаций С(у₁|у₂)=S₁₁–S₁₂S₂₂^–1S₂₁ в выражении (4.5.6) не содержит вектор у₂. С другой стороны, для некоторых распределений отличных от нормального С(у₁|у₂) является функцией у₂.

Если есть только одна переменная у, включённая в вектор v, разделённый в виде v^T=[у, x₁, x₂,..., x_q] = [у, х^T], то его вектор средних m и ковариационная матрица S имеют вид

m= и S=,

где y и s_у² среднее и дисперсия переменной у, s_ух^Т= [s_у1, s_у2,..., s_уq] содержит ковариации s_уi=С(у, x_i) и S_xx содержит дисперсии и ковариации переменных x_i (i=1, 2, …, q). Условное распределение дается в следующем следствии к теореме 4.5.5.

Следствие 1. Если вектор v^T= [у, x₁, x₂,..., x_q] = [у, х^T] имеет вектор средних

m= и матрицу ковариаций S=,

то условное распределение у|х нормальное с

E(у|х) =y+s_ух^ТS_хx^–1(х–x)                                          (4.5.8)

и

D(у|х) =s_у²–s_ух^ТS_хx^–1s_ух                                            (4.5.9)

□

В (4.5.9) квадратичная форма s_ух^ТS_хx^–1s_ух≥0, так как S_хx^–1 положительно определённая. Отсюда

D(у|х)≤D(у).                                                  (4.5.10)

Пример 4.5.7. Демонстрируя применение теоремы 4.5.5, пусть вектор v случайных переменных распределен в виде N₄(m, S), где

m= и S=.

Если вектор v разделён в виде v^Т= [y₁, y₂, x₁, x₂], то y=, x=, S_yy=, S_yх=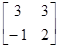 и S_хх=. В силу (4.5.5), получаем

E(у|х) =y+S_yxS_хx^–1(х–x)

=+

=+

=.

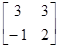
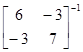
В силу (4.5.6), имеем

С(у|х) =S_yу–S_yxS_хx^–1S_ху

=–

=–

=.

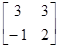
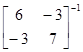
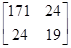
Таким образом, условное распределение у|х имеет вид

N₂.

□

Пример 4.5.8. Для применения следствия 1 теоремы 4.5.5, пусть вектор v~N₄(m, S), где m и S такие, как дано в примере 4.5.7. Если v разделяется так v^Т= [у, x₁, x₂, x₃], то m и S разделяются следующим образом:

m== и S==.

В силу (4.5.8), имеем

E(у|x₁, x₂, x₃) =y+s_ух^ТS_хx^–1(х–x)

=2+[0, 3, 3]

=95/7–12x₁/7+6x₂/7+9x₃/7.

В силу (4.5.9), получаем

D(у|x₁, x₂, x₃) =s_у²–s_ух^ТS_хx^–1s_ух

=9–[0, 3, 3]

=9–45/7=18/7.

Следовательно, условное распределение переменной у|x₁, x₂, x₃ имеет вид N(95/7–12x₁/7 +6x₂/7+9x₃/7, 18/7). Обратим внимание, что D(у|x₁, x₂, x₃) =18/7 меньше чем D(у) =9, что подтверждает неравенство (4.5.10).

□

Упражнения

4.1. Покажите, что E(z) =0 и D(z) =1, когда z имеет стандартную нормальную функцию (4.1.1) плотности вероятности.

4.2. Покажите, что =E(у), где  означает, что  определяется при t=0.

4.3. Рассмотрим некоторую случайную переменную с функцией М(t) производящей моменты её распределения. Покажите, что оцениваемая при t=0 вторая производная от ln[М(t)] является дисперсией этой случайной переменной.

4.4. Полагая, что вектор у имеет распределение N_p(y, s²I) и матрица M ортогональная, покажите, что вектор Mу распределён в виде N_p(My, s²I).

4.5. Пусть A=[I_r, O], как определено в доказательстве теоремы 4.5.3. Покажите, что Ау=y₁, Ay=y₁ и ASA^T=S₁₁.

4.6. Докажите теорему 4.5.5 посредством прямой оценки выражения (4.5.7).

4.7. Положим, что у имеет распределение в виде N₄(y, S), где

y=,        S=.

Найдите следующее:

1. Совместное безусловное распределение y₁ и y₃

2. Безусловное распределение у₂

3. Распределение x=y₁+2y₂–y₃+3y₄

4. Совместное распределение x₁=y₁+y₂–y₃–y₄ и x₂= –3y₁+y₂+2y₃–2y₄

5. f(y₁, y₂|y₃, y₄)

6. f(y₁, y₃|y₂, y₄)

7. r₁₃

8. r_13-24

9. f(y₁|y₂, y₃, y₄).

4.8. Пусть вектор у имеет распределение в виде N₃(y, S), где y= и S=.

Найдите следующее:

1. Распределение x=4y₁–6y₂+y₃

Вам также может быть полезна лекция "Черты эпического стиля в литературе XI-XIII вв".

2. Распределение x=

3. f(y₂|y₁, y₃)

4. f(y₁, y₂|y₃)

5. r₁₂ и r_12-3.

4.9. Если вектор у распределён в виде N₃(y, S), где S=, то какие переменные в у являются независимыми? (cм. следствие 1 теоремы 4.5.2)

4.10. Если вектор у имеет распределение в виде N₄(y, S), где S=, то какие переменные являются независимыми?