Основные задачи, связанные с плоскостью

  §15. Основные задачи, связанные с плоскостью.

I. Условия параллельности, перпендикулярности, угол между плоскостями.

Даны две плоскости: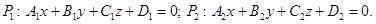

Все перечисленные условия следуют из геометрического смысла коэффициентов (§13).

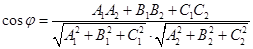
II. Расстояние от точки до плоскости.

Вычисляется так же, как в случае прямой на плоскости (§5).  Пусть произвольная точка пространства. Расстояние от точки до плоскости равно модулю проекции

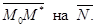
      После простых преобразований получим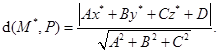

Рекомендуемые материалы

 (#) III.  Связка  и пучок плоскостей.

 Определение1. Множество плоскостей, проходящих через единственную общую точку  М₀ , называется связкой плоскостей с центром в т. М₀  ( Обозначение − S(M₀)).

      Рассмотрим три плоскости, принадлежащие  S(M₀):

                                     ……………………..(*)

Теорема.  Уравнение   описывает связку плоскостей с центром в данной точке.

{Нужно доказать 2 утверждения: 1)  2) .

1) Так как все слагаемые  Q  равны нулю в т. М₀ , то и Q = 0  в этой точке.

2) Так как  СЛАУ (*) имеет единственное решение  (x₀,y₀,z₀), то из правила Крамера следует,

Обратите внимание на лекцию "Обобщенные характеристики МП 8080".

 что определитель системы отличен от нуля, т.е. векторы   линейно независимы и

 . Значение  D = D^* , т.к. все плоскости проходят через т. М₀ }

Определение2. . Множество плоскостей, проходящих через общую прямую – ось плоскостей,

называется пучком плоскостей.

Теорема. Уравнение пучка плоскостей имеет вид:

, при условии