Сформулировать теоремы о связи типа особой точки с видом лорановского разложения и некоторые доказать
Сформулировать теоремы о связи типа особой точки с видом лорановского разложения. И некоторые доказать.
Рядом Лорана называется ряд  =
=  +
+ .
.
Второе слагаемое представляет собой степенной ряд и, как всякий степенной ряд, сходится в круге  . Это слагаемое называется правильной частью ряда Лорана и является, как сумма степенного ряда аналитической функцией.
. Это слагаемое называется правильной частью ряда Лорана и является, как сумма степенного ряда аналитической функцией.
Первое слагаемое называется главной частью ряда Лорана. Делая в нем замену  , запишем главную часть в виде
, запишем главную часть в виде  . Относительно переменной t
. Относительно переменной t
это – степенной ряд, сходящийся в некотором круге  . Возвращаясь к переменной z, получим, что главная часть сходится во внешности круга, радиуса r:
. Возвращаясь к переменной z, получим, что главная часть сходится во внешности круга, радиуса r:
 . Ряд Лорана сходится в области, представляющей собой пересечение областей сходимости правильной и главной частей. Поэтому область сходимости ряда Лорана представляет собой круговое кольцо
. Ряд Лорана сходится в области, представляющей собой пересечение областей сходимости правильной и главной частей. Поэтому область сходимости ряда Лорана представляет собой круговое кольцо  . Радиусы сходимости r, R определяются для степенных рядов обычным образом, сходимость на границах кольца также исследуется, как в степенных рядах. Кольцо может быть вырождено, представлять собой окружность, если r = R или пустое множество, если r > R.
. Радиусы сходимости r, R определяются для степенных рядов обычным образом, сходимость на границах кольца также исследуется, как в степенных рядах. Кольцо может быть вырождено, представлять собой окружность, если r = R или пустое множество, если r > R.
Теорема. Для того чтобы  была правильной точкой функции
была правильной точкой функции  , необходимо и достаточно, чтобы функции
, необходимо и достаточно, чтобы функции  была ограниченной в окрестности точки
была ограниченной в окрестности точки  .
.
Доказательство. Необходимость. Если  - правильная точка функции
- правильная точка функции  , то, доопределяя ее в точке
, то, доопределяя ее в точке  , сделаем функцию аналитической, следовательно, и непрерывной, (тогда
, сделаем функцию аналитической, следовательно, и непрерывной, (тогда  ). Непрерывная функция является ограниченной в некоторой окрестности точки
). Непрерывная функция является ограниченной в некоторой окрестности точки .
.
Достаточность. Пусть функция  - аналитическая в проколотой окрестности точки
- аналитическая в проколотой окрестности точки 
 и ограничена в окрестности
и ограничена в окрестности  .
.
Рекомендуемые материалы
Так как функция  аналитическая в круговом кольце
аналитическая в круговом кольце  , то по теореме Лорана ее можно разложить в этом кольце в сходящийся ряд Лорана
, то по теореме Лорана ее можно разложить в этом кольце в сходящийся ряд Лорана  . Справедливы неравенства Коши
. Справедливы неравенства Коши  . Рассмотрим
. Рассмотрим  .
.  . Следовательно,
. Следовательно,  .
. Тогда ряд Лорана для функции
Тогда ряд Лорана для функции  превращается в ряд Тейлора
превращается в ряд Тейлора  . Доопределим функцию в точке
. Доопределим функцию в точке 
 .Тогда функция
.Тогда функция  станет аналитической в окрестности
станет аналитической в окрестности  как сумма степенного ряда. Поэтому точка
как сумма степенного ряда. Поэтому точка  - правильная точка функции
- правильная точка функции  .
.
Следствие. Разложение функции в ряд Лорана в окрестности правильной точки представляет собой ряд Тейлора и не содержит членов с отрицательными степенями.
Теорема. Для того чтобы точка 
 была полюсом n-го порядка функции
была полюсом n-го порядка функции  , необходимо и достаточно, чтобы ее разложение в ряд Лорана по степеням
, необходимо и достаточно, чтобы ее разложение в ряд Лорана по степеням  не содержало степеней ниже (-n) и содержало слагаемое
не содержало степеней ниже (-n) и содержало слагаемое  .
.
Доказательство. Необходимость. Если точка 
 - полюс n-го порядка функции
- полюс n-го порядка функции  , то
, то  . Разложим аналитическую функцию
. Разложим аналитическую функцию  в ряд Тейлора
в ряд Тейлора  по степеням
по степеням  и подставим разложение.
и подставим разложение.  .
.  .
.
Достаточность. Пусть  . Тогда
. Тогда
 , где
, где 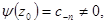
 - аналитическая в точке
- аналитическая в точке  функция (как сумма степенного ряда). Поэтому
функция (как сумма степенного ряда). Поэтому  - полюс n-го порядка функции
- полюс n-го порядка функции  .
.
Теорема. Разложение функции в ряд Лорана в окрестности существенно особой точки конечной плоскости  содержит бесконечное количество отрицательных степеней
содержит бесконечное количество отрицательных степеней  .
.
Доказательство. Если разложение в ряд Лорана в окрестности особой точки конечной плоскости  не содержит отрицательных степеней, то точка
не содержит отрицательных степеней, то точка  - правильная (доказанная выше теорема) - противоречие. Если разложение в ряд Лорана содержит конечное число отрицательных степеней, то точка
- правильная (доказанная выше теорема) - противоречие. Если разложение в ряд Лорана содержит конечное число отрицательных степеней, то точка  - полюс (.доказанная выше теорема) - противоречие. Остается только вариант наличия в разложении бесконечного числа слагаемых с отрицательными степенями.
- полюс (.доказанная выше теорема) - противоречие. Остается только вариант наличия в разложении бесконечного числа слагаемых с отрицательными степенями.
Классификация особой точки  (конечной плоскости) функции
(конечной плоскости) функции  по ее разложению в ряд Лорана в окрестности этой точки.
по ее разложению в ряд Лорана в окрестности этой точки.
Если разложение функции  в ряд Лорана в окрестности
в ряд Лорана в окрестности  (по степеням
(по степеням  ):
):
1. Не содержит отрицательных степеней, то  - правильная точка
- правильная точка  .
.
2. Содержит конечное число отрицательных степеней, то  - полюс
- полюс  , причем наинизшая отрицательная степень определяет порядок полюса.
, причем наинизшая отрицательная степень определяет порядок полюса.
3. Содержит бесконечное количество членов с отрицательными степенями, то  - существенно особая точка
- существенно особая точка  .
.
Это следует из доказанных выше теорем.
Классификация бесконечно удаленной особой точки 
 функции
функции  по ее разложению в ряд Лорана в окрестности этой точки.
по ее разложению в ряд Лорана в окрестности этой точки.
Разложение в ряд Лорана в окрестности точки 
 , т.е. в области
, т.е. в области  представляет собой ряд Лорана по степеням z:
представляет собой ряд Лорана по степеням z:  , в котором главная часть, определяющая особенности функции, содержит положительные степени, а правильная часть – отрицательные степени.
, в котором главная часть, определяющая особенности функции, содержит положительные степени, а правильная часть – отрицательные степени.
Если разложение в ряд Лорана в окрестности точки 
 , т.е. в области
, т.е. в области  :
:
1 Не содержит положительных степеней, то 
 - правильная точка
- правильная точка  .
.
2 Содержит конечное число положительных степеней, то 
 - полюс
- полюс  , причем наивысшая положительная степень определяет порядок полюса.
, причем наивысшая положительная степень определяет порядок полюса.
3 Содержит бесконечное количество членов с положительными степенями, то 
 - существенно особая точка
- существенно особая точка  .
.
Примеры.
Вместе с этой лекцией читают "13 - Бактериологический состав и радиоактивность".
1  . Это и есть разложение в ряд Лорана в окрестности точки
. Это и есть разложение в ряд Лорана в окрестности точки 
 , т.е. в области
, т.е. в области  , поэтому
, поэтому 
 - полюс
- полюс  второго порядка.
второго порядка.
2  . Разложение по степеням
. Разложение по степеням  :
:  справедливо в области
справедливо в области  , т.е. в окрестности точки
, т.е. в окрестности точки 
 . Оно содержит бесконечное количество членов с положительными степенями, поэтому
. Оно содержит бесконечное количество членов с положительными степенями, поэтому 
 - существенно особая точка
- существенно особая точка  .
.
3  . Запишем разложение в окрестности точки
. Запишем разложение в окрестности точки 
 , т.е. в области
, т.е. в области  .
.
 . Разложение не содержит положительных степеней
. Разложение не содержит положительных степеней  , поэтому точка
, поэтому точка 
 - правильная, точнее, нуль первого порядка.
- правильная, точнее, нуль первого порядка.
4.  . Запишем разложение по степеням
. Запишем разложение по степеням  в окрестности точки
в окрестности точки 
 .
. 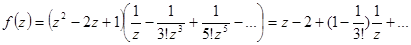
В разложении старшая положительная степень – первая, поэтому 
 - полюс первого порядка. Это же разложение справедливо в области
- полюс первого порядка. Это же разложение справедливо в области  , поэтому оно является разложением в окрестности точки
, поэтому оно является разложением в окрестности точки  . В нем бесконечное количество отрицательных степеней, поэтому точка
. В нем бесконечное количество отрицательных степеней, поэтому точка  - существенно особая.
- существенно особая.






















