Абсолютная непрерывность вероятностных мер, соответствующих скачкообразным процессам
§15 Абсолютная непрерывность вероятностных мер, соответствующих скачкообразным процессам.
15.1. Определение. Пусть на измеримом пространстве  заданы две вероятностные меры
заданы две вероятностные меры  , i = 1,2. Будем говорить, что мера
, i = 1,2. Будем говорить, что мера  абсолютно непрерывна относительно меры
абсолютно непрерывна относительно меры  и обозначать
и обозначать  , если из того, что
, если из того, что  следует, что
следует, что  .
.
Из этого определения следует: если  , то
, то
 . Очевидно, что достаточным условием
. Очевидно, что достаточным условием  является следующее:
является следующее:  для
для  .
.
Из теоремы Радона - Никодима следует, что если  , то существует F - измеримая функция
, то существует F - измеримая функция  такая, что
такая, что  , которую называют производной Радона - Никодима и обозначают
, которую называют производной Радона - Никодима и обозначают .
.
Везде ниже интеграл по мере  будем обозначать через
будем обозначать через  .
.
Пусть имеется измеримое пространство  с фильтрацией
с фильтрацией  , на котором заданы две вероятностные меры
, на котором заданы две вероятностные меры  , i = 1,2. Через
, i = 1,2. Через  обозначим сужение меры
обозначим сужение меры  на
на  , т. е.
, т. е.  . Пусть
. Пусть  , тогда существует в силу теоремы Радона – Никодима
, тогда существует в силу теоремы Радона – Никодима  - процесс
- процесс  называемый локальной плотностью
называемый локальной плотностью  .
.
Теорема 48. Пусть  - локальная плотность. Тогда
- локальная плотность. Тогда  неотрицательный мартингал относительно меры
неотрицательный мартингал относительно меры  , причем
, причем  для
для  .
.
Рекомендуемые материалы
Доказательство. Пусть  и
и  . В силу условий теоремы
. В силу условий теоремы  поэтому
поэтому  . Так как
. Так как  , то
, то 
 . Значит
. Значит
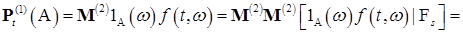
 .
.
Отсюда в силу произвольности  получаем, что
получаем, что 
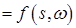
 - п. н. Для завершения доказательства осталось заметить, что при
- п. н. Для завершения доказательства осталось заметить, что при 
 для
для 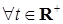 .
.
15.3. Рассмотрим опциональный случайный процесс  , опреде-ленный на стохастическом базисе
, опреде-ленный на стохастическом базисе  со значениями в
со значениями в  и для
и для  Р - п. н. допускающий представление
Р - п. н. допускающий представление
 , (17)
, (17)
где  опциональный случайный процесс с кусочно-постоянными траекториями и неслучайной
опциональный случайный процесс с кусочно-постоянными траекториями и неслучайной  матрицей интенсивности перехода
матрицей интенсивности перехода  , причем
, причем  ;
;  :
:  - предсказуемая случайная функция такая, что
- предсказуемая случайная функция такая, что
Р - п. н.  для
для  .
.
Сначала заметим, что  - предсказуемый процесс, так как
- предсказуемый процесс, так как
 - опциональный. Из свойств интегралов, стоящих в правой части (17) следует
- опциональный. Из свойств интегралов, стоящих в правой части (17) следует


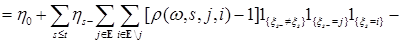
 . (18)
. (18)
Пусть  - последовательность марковских моментов, исчерпывающая скачки процесса
- последовательность марковских моментов, исчерпывающая скачки процесса  , ясно, что: а)
, ясно, что: а)  ; б)
; б)  на множестве
на множестве  ; в)
; в) 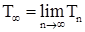
 . Тогда последнее равенство (18) можно записать в виде
. Тогда последнее равенство (18) можно записать в виде


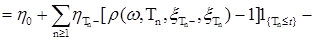
 . (18а)
. (18а)
Отсюда следует, что в момент времени  происходит скачек у процесса
происходит скачек у процесса  и его величина вычисляется по формуле
и его величина вычисляется по формуле  . Поэтому Р - п. н.
. Поэтому Р - п. н.
 . (19)
. (19)
Пусть  , из (18) следует, что Р - п. н.
, из (18) следует, что Р - п. н.
 .
.
Очевидно, что
 .
.
Далее в силу (18), имеем
 .
.
Заметим, что
 .
.
Поэтому
 ×
×
 .
.
Продолжая этот процесс далее, получаем, что P – п.н.
 ,(20)
,(20)
который является решением этого уравнения.
Легко показать, что
1)  если выполняются условия:
если выполняются условия:
а) Р - п. н.  , б) для
, б) для  Р - п. н.,
Р - п. н.,
в)  для
для  Р- п. н.;
Р- п. н.;
2)  если выполняются условия:
если выполняются условия:
а) Р - п. н.  , б) для
, б) для  Р -п. н., в) для
Р -п. н., в) для 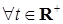
Р - п. н.  ;
;
3)  если выполняются условия:
если выполняются условия:
а)  Р - п. н., б) для
Р - п. н., б) для  Р - п. н.,
Р - п. н.,
в) для 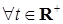 Р - п. н.
Р - п. н.  .
.
Таким образом, доказано утверждение.
Теорема 49. Пусть выполнены условия 1) , 3). Тогда уравнение (17) имеет единственное положительное решение, которое имеет вид (19), причем если выполнено условие 2), то Р - п. н.  для
для 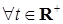 . Кроме того, если
. Кроме того, если  , то для
, то для 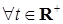 и
и  и является равномерно интегрируемым мартингалом (относительно меры Р).
и является равномерно интегрируемым мартингалом (относительно меры Р).
Замечание. Из теоремы 49 следует, что с помощью процесса  можно определить вероятностную меру
можно определить вероятностную меру  , где
, где  . Очевидно,
. Очевидно,  , а
, а  - производная Радона – Никодима меры Q относительно меры P.
- производная Радона – Никодима меры Q относительно меры P.
15.4. Теорема 50 (Гирсанов). Пусть  опциональный случайный процесс с конечным или счетным множеством состояний Е и матрицей интенсивности перехода
опциональный случайный процесс с конечным или счетным множеством состояний Е и матрицей интенсивности перехода  . Пусть
. Пусть  удовлетворяет условиями 1)-3) теоремы 44. Тогда относительно меры
удовлетворяет условиями 1)-3) теоремы 44. Тогда относительно меры  , где
, где  процесс
процесс  - опциональный с конечным или счетным числом состояний и матрицей интенсивности перехода
- опциональный с конечным или счетным числом состояний и матрицей интенсивности перехода  .
.
Доказательство. Пусть  - целочисленная случайная мера, построенная по скачкам процесса
- целочисленная случайная мера, построенная по скачкам процесса  . Из условий теоремы следует, что ее компенсатор относительно меры P имеет вид
. Из условий теоремы следует, что ее компенсатор относительно меры P имеет вид  , т. е.
, т. е.  является мартингалом относительно меры Р. Нам надо показать, что относительно меры Q процесс
является мартингалом относительно меры Р. Нам надо показать, что относительно меры Q процесс  - мартингал относительно потока
- мартингал относительно потока  , т. е. Q - п. н.
, т. е. Q - п. н.  . Последнее равенство выполнено тогда и только тогда, когда
. Последнее равенство выполнено тогда и только тогда, когда  для
для  . Из определения меры Q следует
. Из определения меры Q следует
 .
.
Из свойств условного математического ожидания, в силу того, что
 - измеримо, имеем
- измеримо, имеем
 .
.
Учитывая, что  - равномерно интегрируемый мартингал относительно меры Р, имеем
- равномерно интегрируемый мартингал относительно меры Р, имеем
 .
.
Применим теперь формулу Ито для произведения мартингалов
 , имеем P - п. н.
, имеем P - п. н.
 .
.
Рассмотрим  . Очевидно, что
. Очевидно, что
 ,
,  .
.
Поэтому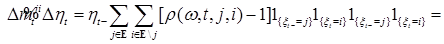
 .
.
Значит


 .
.
Ещё посмотрите лекцию "9 Оператор присваивания" по этой теме.
Таким образом, имеем
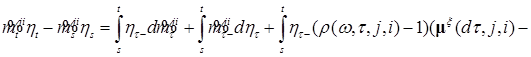
 . (21)
. (21)
Заметим, что второе и третье слагаемые правой части (21) являются стохастическими интегралами по мартингалам, имеющим ограниченную вариацию. Поэтому они являются мартингалами относительно меры Р, имеем
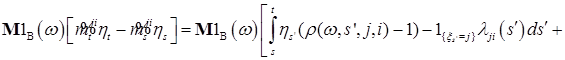
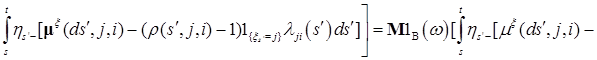
 .
.
Доказательство закончено.




















