Случайные меры и мультивариантные точечные процессы

§14 Случайные меры и мультивариантные точечные процессы.

14.1. Пусть - m - вариантный точечный процесс, a

 , - считающие процессы, где .

Пример. Пусть 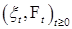- случайный процесс определённый соотно­шением   - пуассоновский случайный процесс с интенсивностью . Ясно, что процесс принимает два значения {-1, 1}, причём время пребывания в состоянии -1 или в состоянии 1 распределены экспонен-циально с параметром . Этот процесс имеет кусочно-постояные траектории и непрерывен справа, поэтому он опционален. Через  обозначим число попаданий в состояние 1(-1) за время t процессом 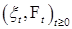. Очевидно, что если   для  , то  можно построить следующим образом:

,

.

Ясно также, что с помощью  и  можно описать процесс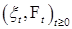

,

Рекомендуемые материалы

так как . Легко показать, что для 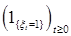 справедливо предста­вление

,

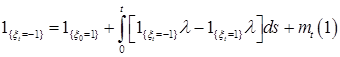
причем  - ограниченные мартингалы (относительно меры Р)  для .

Приведённый выше пример служит основой для дальнейших построений.

14.2. Перейдем теперь к построению целочисленной случайной меры k - вариантного точечного процесса и её компенсатора.

В предыдущих параграфах мы установили связь между скачко-образными и мультивариантными точечными процессами. Итак, пусть 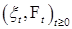 - скачкообразный опци­ональный случайный процесс со значениями в Е, причём . В соответствии с результатами параграфа 13 для процесса определена целочисленная случайная мера , где - последовательность марковских моментов, исчерпывающая скачки процесса ,  . Очевидно, что при фиксированных   это опциональный неубывающий процесс, т. е.  при t ³ s. Стало быть,  является субмартингалом и по теореме Дуба-Мейера существует компенсатор ,  т. е.  является мартингалом относительно потока и меры Р. Предположим дополнительно, что 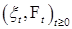 имеет неслучай­ную матрицу интенсивности перехода . Тогда в силу теоремы 35 допускает представление:

.                                             (9)

Обозначим  - число переходов процесс из состояния j в состояние i за время t. Ясно, что его можно представить в виде:

.

Найдём компенсатор  - случайной меры . Сначала заметим, что

.

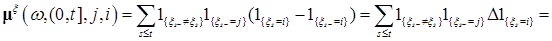
Отсюда, в силу (9), имеем:

.            (16)

Заметим: 1) для  Р - п. н.

;

2) так как  - ограниченный предсказуемый процесс, то

стохастический инте­грал  является мартингалом. Поэтому процесс  является компенсатором  - целочисленной случайной меры относительно меры P.

Очевидно, что

Dx_t = x_t - x_t- =  . Учитывая, что траектория процесса  кусочно-постоянна, получаем, . Поэтому

.

Таким образом, доказано утверждение.

Теорема 47. Пусть  опциональный процесс с кусочно-постоянными траекториями, конечным или счетным множеством состояний Е и матрицей интенсивности переходов  размера - . Тогда справедливы следующие утверждения:

1) целочисленная случайная мера  допускает представление  ,

где - последовательность марковских моментов (опциональных), исчерпывающая скачки процесса ;

2) компенсатор  целочисленной случайной меры  имеет вид

Ещё посмотрите лекцию "7 Мероприятия по регулированию выбросов при неблагоприятных метеорологических условиях" по этой теме.

;

3) процесс  допускает представление

 .

14.3. Замечание. В общем случае, если - опциональный скачкообразный процесс с кусочно-постоянными траекториями, со значениями в ,  как легко показать, допускает представление

x_t = x₀ + ,

где .