Классификация марковских цепей по асимптотическим свойствам

§10 Классификация марковских цепей по асимптотическим свойствам.

10.1. Пусть - марковская цепь. Обозначим - марковский момент первого попадания в состояние  после момента времени , т. е. . Обозначим

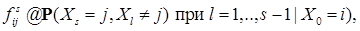
Очевидно, что  при  это переходная вероятность за один шаг из состояния  в .

Обозначим .

Предложение 44.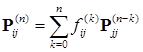

Доказательство. Пусть  - момент первого попадания в состояние . Из этого определения следует, что . Очевидно, что , так как

Рекомендуемые материалы

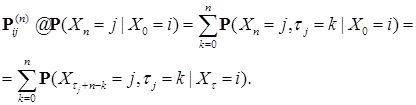
Заметим, что , поэтому в силу строго марковского свойства, имеем

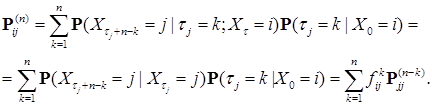
Доказательство закончено.

10.2. Обозначим - вероятность того, что за бесконечное число шагов однородная марковская последовательность  попадет из состояния  в .

Определение. Состояние  называется возвратным, если . Если , то состояние называется невозвратным.

Определение.  называется средним временем до возвращения в состояние . Говорят, что состояние  положительно, если . Состояние  называется нулевым, если .

Теорема 45 (критерий возвратности). 1) Пусть имеется однородная марковская цепь (ОМЦ). Состояние  возвратно тогда и только тогда, когда .

2) Если  - возвратное состояние и   сообщается с , то  - возвратное состояние.

Доказательство. 1) Так как , то

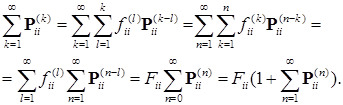
Вам также может быть полезна лекция "2.4. Двоичные числа в дополнительном коде".

 Значит

.

Отсюда следует, что  тогда и только тогда, когда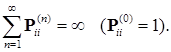

Утверждение ii) очевидным образом следует из i).

Следствие 46. Если ряд  сходится, то состояние  - невозвратное.