Эргодические марковские цепи

§11 Эргодические марковские цепи.

11.1. Определение. Однородная марковская последовательность называется эргодической, если существует предел , который не зависит от состояния  и выполняются условия:

1) , 2)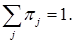

Замечание. Эргодические процессы, в отличие от обычных марковских процессов, "не помнят" точку старта.

Теорема 47 (достаточные условия существования эргодического распределения). Пусть - переходная вероятность за один шаг. Пусть существует  такое, что . Тогда существует вектор , компоненты которого  и , причем для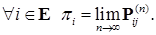

Доказательство. Из соотношения Чепмена-Колмогорова, имеем

.

Обозначим:  Покажем, что  при . Действительно
,т. е. .

Аналогично устанавливается неравенство .

Рекомендуемые материалы

Из соотношения Чепмена - Колмогорова следует, что

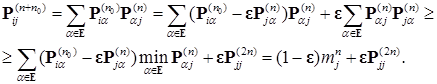
Таким образом для  и , имеем  отсюда следует неравенство

.                                                               (27)

Аналогичным образом легко показать

                                                              (28)

Вычтем из (27) (28), имеем . Выбирая  кратное  (например ), получаем, что . Отсюда следует  при .

Доказательство закончено.

11.2. Теорема 48. Пусть имеется однородная марковская цепь , а - переходная вероятность за один шаг. Пусть . Тогда

1) ;

2)  либо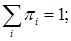

3) если , то эргодического распределения не существует;

4) если   то эргодическое распределение существует и единственно.

Доказательство. 1) .В силу леммы Фату .Рассмотрим
т. е.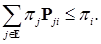

Пусть существует индекс :

 Следовательно

Мы пришли к противоречию. Значит наше предположение неверно, поэтому .                                                                                                        (29)

2) Из утверждения 1) теоремы имеем

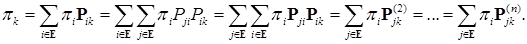
Значит для  

"7. Экстремальные события на производстве" - тут тоже много полезного для Вас.

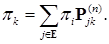
Устремляя в (29) , получаем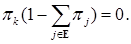

1) Если вектор , то он не является распределением вероятностей. Следовательно пункт 3) - доказан.

2) , следовательно  - распределение вероятностей.

Доказательство закончено.