Функция плотности вероятности многомерного распределения

4.2. Функция плотности вероятности многомерного распределения

Теперь рассмотрим вектор у^Т=[у₁, у₂, ..., у_п] случайных переменных, заданный в n-мерном выборочном пространстве. Понятие непрерывной функции плотности вероятности вектора у случайных переменных вводится следующим образом [Линник (1962) стр.40-41]. Если имеется n-мерный параллелепипед P_d=[у_i, у_i+d_i] (i=1, 2, …, n), где (у₁, у₂, ..., у_n) – координаты любой фиксированной точки, а d_i - любые положительные числа, то можно считать, что определена вероятность Рr(уP_d) нахождения вектора у в параллелепипеде P_d и существует предел

=f(у₁, у₂, ..., у_n),

где f(у₁, у₂, ..., у_n) - непрерывная функция плотности вероятности распределения вектора у. Так как вероятность неотрицательна, то и функция f(у₁, у₂, ..., у_n)≥0.

Если W - некоторая область в n-мерном пространстве, допускающая по ней интегрирование, то вероятность нахождения вектора у в этой области определяется выражением

Рr(уW)=.                        (4.2.1)

А если область W представляет всё n-мерное пространство, то интеграл (4.2.1) равен единице

=1.                    (4.2.2)

Вектор у случайных переменных является обобщением понятия одной случайной переменной на п случайных переменных. Функция (4.1.5) плотности вероятности распределения по нормальному закону одной переменной может быть записана в виде

Рекомендуемые материалы

f(у)=exp[–(у–y)(s²)^–1(у–y)/2].                      (4.2.3)

Здесь выражение (у–y)(s²)^–1(у–y) представляет квадратичную форму от одной случайной переменной. При п случайных переменных можно также найти квадратичную форму от формируемого случайными переменными вектора у в виде (у–y)^TS^–1(у–y), где S - ковариационная матрица и y - вектор средних для случайных переменных вектора у.

В (4.2.3) s² является дисперсией или ковариацией одной случайной переменной (у). Для п случайных переменных ковариационная матрица имеет вид

S=E[(у–y)(у–y)^T].                                                   (4.2.4)

где вектор y средних находится следующим образом

y=Е==.

Матрица S положительно определенная, если и только если существует невырожденная матрица А такая, что S=АА^T. При этом её обратная матрица S^–1 также положительно определенная, так как S^–1=(АА^T)^–1=(А^T)^–1А^–1=(А^–1)^TА^–1=SS^T, где матрица S=(А^–1)^T тоже невырожденная. Таким образом, по аналогии с функцией (4.2.3), функцию плотности вероятности распределенных по нормальному закону п случайных переменных можно записать в виде

f(у₁, у₂, …, у_п)=С₀ехр[–(у–y)^TS^–1(у–y)/2],                          (4.2.5)

где постоянная С₀, в силу (4.2.2), находится из уравнения

С₀=1.       (4.2.6)

Так как матрица S^–1 положительно определенная, то квадратичная форма (у–y)^TS^–1(у–y) неотрицательна и функция f(y₁, у₂, …, y_n) ограничена, имея при y=y максимальное значение С₀. Эта постоянная определяется выражением

С₀=,

где det(S) - определитель матрицы S [Линник (1962) теорема 2.2.1, стр.46-50].  Следовательно, функция плотности вероятности распределения п случайных переменных имеет вид

f(у₁, у₂, …, у_п)=ехр[–(у–y)^TS^–1(у–y)/2].                        (4.2.7)

Это выражение можно использовать для нахождения функции плотности вероятности п случайных переменных, используя вектор y их средних и ковариационную матрицу S с det(S)>0.

Определение 4.1. Распределение, имеющее функцию (4.2.7) плотности вероятности, называется многомерным нормальным распределением.

Функцию (4.2.7) можно получить также, используя функцию плотности вероятности независимых случайных переменных z₁, z₂, ..., z_п, распределённых по стандартному нормальному закону со средними z_i=0, дисперсиями s_i²=1 (i=1, 2, …, п) и ковариациями s_ij=0, где i≠j (j=1, 2, …, п). При этом переменные z₁, z₂, ..., z_п преобразуются в случайные переменные у₁, у₂, ..., у_п, распределённые нормально с произвольными средними, дисперсиями и ковариациями.

Вектор z^T= [z₁, z₂, ..., z_п] случайных переменных имеет E(z)=0 и C(z)=I. В нём каждая переменная имеет стандартное нормальное распределение N(0, 1) и функцию плотности вероятности, данную выражением (4.1.1). Необходимо преобразовать вектор z в вектор у^T= [у₁, у₂, ..., у_п] случайных переменных, распределённых нормально с Е(у)=y и C(у)=S, где y - любой вектор размеров nх1 и S - любая положительно определённая матрица размеров nхn.

В силу (3.2.11) и (4.1.1), имеем

g(z₁, z₂, ..., z_n)=g(z)=g₁(z₁)g₁(z₁)...g_n(z_n)

=exp(–z₁²/2)exp(–z₂²/2)…exp(–z_n²/2)

=exp[–(z₁²+z₂²+…+z_n²)/2]

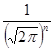=exp(–z^Tz/2).                                                            (4.2.8)

Таким образом, вектор z имеет многомерную нормальную функцию (4.2.8) плотности вероятности, вектор средних Е(z)=0 и матрицу ковариаций C(z)=I или просто имеет стандартное многомерное нормальное распределение z~N_n(0, I), где n - размерность распределения, соответствующая числу переменных в векторе z.

Для преобразования вектора z в вектор у с произвольными вектором средних Е(у)=y и положительно определенной матрицей ковариаций С(у)=S, по аналогии с выражением у=sz+y для одной переменной, определим преобразование в виде

у=S^1/2z+y,                                                     (4.2.9)

где S^1/2 - симметричная матрица квадратного корня, определённая выражением (П.12.17). При таком преобразовании, в силу (3.6.7) и (3.6.12), имеем

Е(у)=Е(S^1/2z+y)=S^1/2Е(z)+y=S^1/20+y=y,

С(у)=С(S^1/2z+y)=S^1/2С(z)(S^1/2)^T=S^1/2I(S^1/2)^T=S.

В силу (4.2.2), кратный интеграл функции (4.2.8) в п-мерном пространстве равен единице

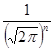
=1.                      (4.2.10)

При вычислении этого интеграла перейдем к переменным у₁, у₂,..., у_n. Областью интегрирования будет снова п-мерное пространство (–∞<у_i<∞). Как известно из теории кратных интегралов, при переходе к новым переменным в (4.2.10) нужно dz₁dz₂...dz_n заменить на dy₁dy₂...dy_n, умноженным на абсолютную величину якобиана |det(J)|, где матрица J=(∂z_i/∂y_j) [Линник (1962) стр.47]. В данном случае, в силу (4.2.9), имеем

Информация в лекции "2.2 Принцип обратной связи" поможет Вам.

z=S^–1/2(y–y),                                                 (4.2.11)

так что производная ∂z/∂y=(S^–1/2)^Т [Searle (1982) стр.329] и ∂z/∂y=S^–1/2, так как S^–1/2 симметричная матрица. Значит матрица J=S^–1/2 и, так как матрица S^–1/2 ещё и положительно определенная, то

|det(J)|=det(S^–1/2).                                         (4.2.12)

Следовательно, замена переменных в интеграле (4.2.10) с использованием выражений (4.2.11), (4.2.12) и (П.12.18) даёт

[det(S)]^–1/2=1,

где функция под интегралом такая же, как и в (4.2.7).