Линейные формы
Линейные формы
Как мы уже знаем, линейный функционал - это линейное отображение некоторого линейного пространства  в
в  - множество вещественных чисел, рассматриваемое как одномерное арифметическое пространство. Предполагая всюду в дальнейшем, что
- множество вещественных чисел, рассматриваемое как одномерное арифметическое пространство. Предполагая всюду в дальнейшем, что  конечномерно (
конечномерно ( ), рассмотрим более подробно структуру пространства
), рассмотрим более подробно структуру пространства  , называемого сопряженным пространством (см. п. 1.8).
, называемого сопряженным пространством (см. п. 1.8).
Утверждение 1.17 Для всякого линейного функционала  и любого произвольно фиксированного базиса
и любого произвольно фиксированного базиса  в пространстве
в пространстве  однозначно определен вектор-строка
однозначно определен вектор-строка  такой, что для всякого
такой, что для всякого 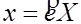
 .
.
Доказательство. Действительно,  ,
,
где строка  имеет вид:
имеет вид:
 ,
,
представляя собой, очевидно, строку значений функционала  на базисных векторах пространства
на базисных векторах пространства  (ее можно рассматривать как обычную в такой ситуации векторную матрицу-строку, состоящую из векторов размерности 1, т.е., просто чисел).
(ее можно рассматривать как обычную в такой ситуации векторную матрицу-строку, состоящую из векторов размерности 1, т.е., просто чисел).
В сущности, строка  есть не что иное, как матрица линейного оператора
есть не что иное, как матрица линейного оператора  , принимающего значения в одномерном пространстве.
, принимающего значения в одномерном пространстве.
Рекомендуемые материалы
Представление линейного функционала  в виде
в виде  называют линейной формой.
называют линейной формой.
Покажем, что на самом деле линейная форма есть разложение представляемого ею функционала по некоторому базису сопряженного пространства.
Относительно фиксированного базиса  пространства
пространства  введем функционалы
введем функционалы  следующим образом:
следующим образом:
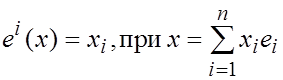
Линейность функционалов  легко проверяется. Тогда произвольный линейный функционал
легко проверяется. Тогда произвольный линейный функционал  может быть представлен в виде:
может быть представлен в виде:
 (1)
(1)
Подчеркнем, что формула (1) дает выражение для самого функционала, а не для его значения на каком-то векторе - это запись линейной комбинации функционалов из сопряженного пространства. Числа  , компоненты строки
, компоненты строки  образуют коэффициенты данной линейной комбинации. Значение же функционала
образуют коэффициенты данной линейной комбинации. Значение же функционала  на произвольном векторе
на произвольном векторе 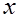 будет тогда выражаться в виде:
будет тогда выражаться в виде:
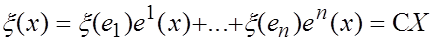
Тем самым доказана теорема:
Теорема 1.7 Функционалы  , образуют базис сопряженного пространства
, образуют базис сопряженного пространства  (он называется базисом, сопряженным к базису
(он называется базисом, сопряженным к базису  пространства
пространства  ). Тем самым
). Тем самым  .
.
Выясним теперь, как преобразуются координаты линейного функционала в сопряженном базисе при преобразовании базиса исходного пространства  .
.
Перепишем (1) в виде:
 (2)
(2)
где  .
.
Введем в  новый базис
новый базис  , где
, где  - матрица перехода.
- матрица перехода.
Тогда
 ,
,
откуда
 (3)
(3)
или ( с учетом (2)):
 (4)
(4)
Из (3) и (4) видно, что координаты ковектора (линейного функционала) в сопряженном базисе преобразуются при переходе от одного базиса исходного пространства  к другому не как координаты вектора из
к другому не как координаты вектора из  , а как сами базисы
, а как сами базисы  . Эта «зеркальность» закона преобразования координат ковекторов по сравнению с законом преобразования координат самих векторов (в данном случае, элементов пространства
. Эта «зеркальность» закона преобразования координат ковекторов по сравнению с законом преобразования координат самих векторов (в данном случае, элементов пространства  ) и обусловила сам термин «ковектор» (двойственный, сопряженный вектор).
) и обусловила сам термин «ковектор» (двойственный, сопряженный вектор).
Обсудим теперь вопрос о линейных формах в евклидовом пространстве.
Теорема 1.8 Для любого линейного функционала  , определенного на конечномерном евклидовом пространстве
, определенного на конечномерном евклидовом пространстве  может быть однозначно определен такой вектор
может быть однозначно определен такой вектор  , что
, что  .
.
Доказательство. Согласно утверждению 1.16 имеем:
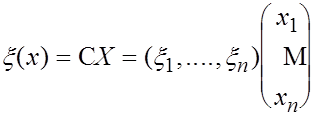
Тогда, полагая, что базис  в
в  является ортонормированным, получим, вводя вектор
является ортонормированным, получим, вводя вектор  как
как  , что
, что  .
.
Поскольку по теореме об ортогонализации (теорема 1.1, п. 1.6) любой базис евклидова пространства может быть преобразован к ортонорму (т.е., ортонормированному базису), приведенные выше рассуждения не зависят от выбора конкретного базиса.
Докажем теперь единственность вектора  . Пусть для данной линейной формы существует еще какой-то вектор
. Пусть для данной линейной формы существует еще какой-то вектор  , такой, что
, такой, что  . Тогда для любого
. Тогда для любого 
 ,
,
Рекомендуем посмотреть лекцию "Модернизм".
откуда  .
.
Теорема доказана.
Обратим как раз внимание на инвариантность формулировки теоремы 1.8: представление линейного функционала в евклидовом пространстве как скалярного произведения некоторого постоянного вектора на переменный вектор (векторный аргумент) не зависит от выбора конкретного базиса, но следует, однако, иметь в виду, что равенство  имеет место, конечно, только при разложении векторов по ортонормированному базису.
имеет место, конечно, только при разложении векторов по ортонормированному базису.
Скалярное произведение  называют линейной формой в евклидовом пространстве. Геометрический смысл линейной формы состоит в том, что уравнение
называют линейной формой в евклидовом пространстве. Геометрический смысл линейной формы состоит в том, что уравнение
 (5)
(5)
определяет в  геометрическое место точек, называемое линейным многообразием. В частности, при
геометрическое место точек, называемое линейным многообразием. В частности, при  получаем плоскость в пространстве, а при
получаем плоскость в пространстве, а при  - прямую на плоскости. В общем случае линейное многообразие, определенное уравнением (5), называется
- прямую на плоскости. В общем случае линейное многообразие, определенное уравнением (5), называется  - мерной гиперплоскостью. Интересно заметить, что линейное многообразие, будучи некоторым подмножеством множества векторов
- мерной гиперплоскостью. Интересно заметить, что линейное многообразие, будучи некоторым подмножеством множества векторов  , не является подпространством в
, не является подпространством в  , если только
, если только  .
.























