Приложение В Разделение матриц

П.3. Разделение матриц

Иногда требуется разделить матрицу на подматрицы. Например, разделение матрицы А на четыре (квадратные или прямоугольные) подматрицы необходимых размеров может быть представлено следующим образом:

А=.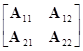

Для примера, пусть матрица А размеров 4х5 разделена на блоки в виде

А==,

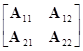где

А₁₁=, А₁₂=, А₂₁= и А₂₂=.

Если матрицы А и В имеют соответствующие размеры для умножения и разделены таким образом, что их подматрицы также имеют соответствующие размеры для умножения, то произведение АВ можно найти с помощью обычной схемы умножения строк на столбцы с подматрицами, как если бы они были единичными элементами, например,

АВ=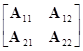

Рекомендуемые материалы

=.     (П.3.1)

Если матрицу B заменить вектором b, разделённым на два подвектора b₁ и b₂, а матрица А разделена соответственно на две подматрицы А₁ и А₂, то произведение Аb можно записать в разделённом виде

Аb=[A₁, A₂]=A₁b₁+A₂b₂,                                (П.3.2)

где число столбцов матрицы A₁ равно числу элементов вектора b₁ и матрица А₂ с вектором b₂ также имеют соответствующие размеры для умножения. Заметим, что разделение матрицы А=[A₁, A₂] обозначается с использованием запятой.

Данное в (П.3.2) умножение разделённых матрицы и вектора может применяться к отдельным столбцам матрицы А и отдельным элементам вектора b:

Аb=[а₁, а₂, …, а_р]=b₁а₁+b₂а₂+…+b_ра_р.          (П.3.3)

Здесь Ab является линейной комбинацией столбцов матрицы А, где коэффициентами служат элементы вектора b. Покажем это в следующем примере.

Пример П.3. Пусть A= и b=, тогда Ab=.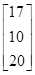

Используя линейную комбинацию столбцов А, как показано в (П.3.3), получаем

Ab=b₁а₁+b₂а₂+b₃а₃=4+2–=+–=

□

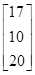
На основании полученных в (П.2.20) и (П.3.3) выражений АВ= [Аb₁, Аb₂, …, Аb_р] и Аb=b₁а₁+b₂а₂+…+b_ра_р столбцы матрицы AB являются линейными комбинациями столбцов матрицы А. Коэффициентами линейной комбинации j-го столбца матрицы AB являются элементы j-го столбца матрицы B.

Произведение вектора строки а_с и матрицы B можно представить в виде линейной комбинации строк матрицы B, в которой коэффициентами являются элементы строки а_с:

Рекомендуем посмотреть лекцию "9 Завершение процесса антропогенеза и расогенез".

а_сB=[а₁, а₂, …, а_n]=а₁b_1с+a₂b_2с+…+a_nb_nс.                 (П.3.4)

Поэтому на основе полученного в (П.2.19) выражения АВ= и (П.3.4) строки матрицы AB являются линейными комбинациями строк матрицы B, а коэффициентами линейной комбинации i-й строки AB являются элементы i-й строки матрицы А.

Наконец отметим, что если матрица A разделена в виде [А₁, А₂], то

A^Т=[А₁, А₂]^Т=                                                 (П.3.5)

и её произведение на саму себя имеет вид

A^ТA=[А₁, А₂]=.                  (П.3.6)