Приложение Б Операции с матрицами
П.2. Операции с матрицами
Определим сумму и произведение матриц, а также рассмотрим некоторые их свойства.
Сумма двух матриц
Если две матрицы имеют одинаковые размеры, то с ними можно выполнить операцию сложения. Сумма матриц находится путем сложения их соответствующих элементов. Так, если А и В размеров nxр, то С=А+B - матрица тех же размеров nxр и находится в виде C=(cij)=(aij+bij), например,
 +
+ =
= .
.
Разность G=А–B двух матриц А и В находится в виде: G=(gij)=(aij–bij).
Два свойства сложения матриц приведены в следующей теореме.
Теорема П.2.1. Если матрицы А и В обе размеров nxm, то
- A+B=B+A. (П.2.1)
- (A+B)Т=AТ+BТ. (П.2.2)
Доказательство: Пункт 1 следует из коммутативности действительных чисел
Рекомендуемые материалы
aij+bij=bij+aij.
Для пункта 2 пусть С=А+В. Тогда, в силу (П.1.3),
СТ=(сij)Т=(сji)=(aji+bji)=(aji)+(bji)=АТ+ВТ.
□
Произведение матрицы на число
Любая матрица может быть умножена на любое скалярное число. Произведение матрицы на скаляр с определяется, как произведение каждого элемента матрицы на этот скаляр
сА=(сaij)= . (П.2.3)
. (П.2.3)
Так как caij=aijc, то произведение скаляра и матрицы коммутативно
cA=Ac. (П.2.4)
Произведение двух матриц
Для того чтобы произведение АВ было определено необходимо чтобы число столбцов матрицы A было равно числу строк матрицы B. Тогда (ij)-й элемент произведения С=АВ находится в виде
cij= , (П.2.5)
, (П.2.5)
что является суммой произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Таким образом, каждая строка матрицы A умножается на каждый столбец матрицы B. Если матрица A размеров nxm и матрица В размеров mxp, то матрица С=АВ получается размеров nxр. Покажем умножение матриц на следующем примере.
Пример П.2.1. Пусть А= и В=
и В= , тогда
, тогда
АВ= =
=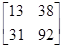
ВА= =
=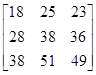
□
Если для матриц А=Аnm и B=Вmр имеем р≠n, то произведение АВ определено, а произведение ВА неопределенно. Для матриц А=Аnр и B=Врn произведение AB имеет размеры nхn, а произведение ВА имеет размеры рхр. В этом случае, конечно АВ≠ВА, как показано в примере П.2.1. Если А и В обе одинаковых размеров nхn, то AB и BA имеют одинаковые размеры, но в общем
АВ≠ВА. (П.2.6)
[Есть несколько исключений из этого правила, например, две диагональные матрицы или квадратная и единичная матрицы.] Таким образом, умножение матриц не является коммутативным и некоторые знакомые операции с вещественными числами не могут быть выполнены с матрицами. Тем не менее, умножение матриц дистрибутивно для их сложения или вычитания:
А(B±C)=AB±AC, (П.2.7)
(A±B)C=AC±BC. (П.2.8)
Используя (П.2.7) и (П.2.8) можно преобразовать произведение (А–B)(C–D) следующим образом
(А–B)(C–D)=(А–B)C–(А–B)D [в силу (П.2.7)]
=АC–BC–АD+BD [в силу (П.2.8)]. (П.2.9)
Умножение матрицы на вектор выполняется по тем же правилам, что и умножение матриц. Положим, что матрица А=Аnр и векторы b=bр1, с=cр1 и d=dn1. Тогда произведения: Ab - вектор размеров nх1, dТA - вектор строка размеров 1хр, bТс - скалярное число, bсТ - матрица размеров рхр и cdТ - матрица размеров рхn. Так как bТс - скалярное число, то оно равно сТb:
bТс=b1с1+b2с2+...+bрср, сТb=с1b1+с2b2+...+срbр, bТс=сТb. (П.2.10)
Матрица cdТ получается в виде
cdТ= . (П.2.11)
. (П.2.11)
Аналогично
bТb=b12+b22+...+bр2, (П.2.12)
bbТ= . (П.2.13)
. (П.2.13)
Таким образом, bТb - сумма квадратов и bbТ - симметричная квадратная матрица.
Квадратный корень из суммы квадратов значений элементов вектора b размеров рх1 является расстоянием от начала координат в пространстве р измерений до точки в этом пространстве, координаты которой определены значениями элементов вектора b. Положительное значение этого квадратного корня является длиной или нормой вектора b:
Длина вектора b= =
= . (П.2.14)
. (П.2.14)
Если 1 - вектор единиц размеров nх1, то, в силу (П.2.12) и (П.2.13), получаем
1Т1=n и 11Т= =E, (П.2.15)
=E, (П.2.15)
где E=Еnn - квадратная матрица размеров nхn. Если вектор а=аn1 и матрица А=Аnр, то
аТ1=1Та= , (П.2.16)
, (П.2.16)
1ТА= и А1=
и А1= . (П.2.17)
. (П.2.17)
Таким образом, аТ1 - сумма элементов вектора а, 1ТА – вектор строка сумм элементов столбцов матрицы A и A1 - вектор столбец сумм элементов строк матрицы А. Заметим, что в аТ1 и 1ТА вектор 1 размеров nх1, а в A1 вектор 1 размеров рх1.
Транспозиция произведения двух матриц равна произведению транспозиций сомножителей в обратном порядке.
Теорема П.2.2. Для матриц А=Аnр и В=Врm имеем
(AB)Т=BТAТ. (П.2.18)
Доказательство дано в [Беклемишев (2006), стр.125].
□
Покажем применение теоремы П.2.2 для матриц А=А23 и B=В32:
AB=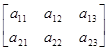
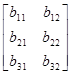
= ,
,
(AB)Т=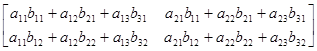
=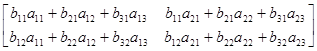
=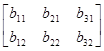
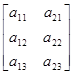
=BТAТ
Если последовательно применять выражение (П.2.18) к произведению любого числа матриц, то получаем
(ABС...Z)Т=ZТ…CТBТAТ.
Любая матрица А может быть умножена на свою транспозицию для образования произведений AТA или AAТ. Некоторые свойства этих двух произведений приведены в следующей теореме.
Теорема П.2.3. Пусть А=Аnр - любая матрица. Тогда произведения AТA и AAТ имеют следующие свойства:
- Матрица AТA имеет размеры рхр и её элементы равны произведениям столбцов А.
- Матрица AAТ имеет размеры nхn и её элементы равны произведениям строк А.
- Обе матрицы AТA и AAТ симметричные.
- Если AТA=O, то А=О.
Доказательство:
Доказательства пунктов 1 и 2 следуют из определения умножения матриц.
3. (AТA)Т=AТ(AТ)Т=AТA и (AAТ)Т=(AТ)ТAТ=AAТ.
4. Число аiTаi является i–м диагональным элементом матрицы AТA, где аi - i-й столбец матрицы А. Так как аiTаi= =0, то имеем аi=0.
=0, то имеем аi=0.
□
Положим, матрицы А=Аnm и В=Вmр. Пусть aiс будет i-й строкой матрицы А, bj будет j-м столбцом матрицы В и эти матрицы можно представить в виде
А= и В=[b1, b2, …, bp].
и В=[b1, b2, …, bp].
Тогда, по определению, (ij)-м элементом произведения AB является aiсbj, то есть,
АВ= .
.
Результат произведения можно записать с использованием строк матрицы А:
АВ= =
= =
= В. (П.2.19)
В. (П.2.19)
С помощью матрицы А первый столбец произведения AB записывается в виде
Ab1= b1=
b1= .
.
Аналогично, второй столбец можно записать в виде Ab2 и так далее. Таким образом, AB можно записать посредством столбцов матрицы B следующим образом:
АВ=А[b1, b2, …, bр]=[Аb1, Аb2, …, Аbр]. (П.2.20)
Пусть матрица A=Аnn и матрица D=диаг[d1, d2,..., dn]. Тогда в произведении DА элементы i-й строки матрицы А умножаются на di, а в произведении AD элементы j-го столбца матрицы А умножаются на dj. Например, если n=3, то имеем
DA=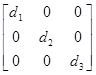
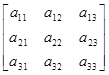 =
= , (П.2.21)
, (П.2.21)
AD=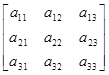
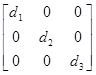 =
= , (П.2.22)
, (П.2.22)
DAD= . (П.2.23)
. (П.2.23)
Обратим внимание, что DA≠AD. Тем не менее, в случае, когда диагональная матрица единичная, то (П.2.21) и (П.2.22) сводятся к выражению
IA=AI=A. (П.2.24)
Если матрица А прямоугольная, то (П.2.24) остается в силе, но единичные матрицы для умножения слева и справа должны быть соответствующих размеров. Это также справедливо и для выражений (П.2.21), (П.2.22) и (П.2.23), где диагональные матрицы также должны быть соответствующих размеров [Беклемишев (2006) стр.126].
Если А - симметричная матрица и у - вектор, то произведение
уТАу= +
+ (П.2.25)
(П.2.25)
называется квадратичной формой. Если векторы х=хn1, у=ур1 и матрица А=Аnр, то произведение
хТАу= (П.2.26)
(П.2.26)
называется билинейной формой.
Произведение Адамара
Обратите внимание на лекцию "Сарматы".
Иногда применяется третий тип произведения матриц, называемый поэлементным или произведением Адамара. Если две матрицы или два вектора имеют одинаковые размеры, то их произведение Адамара находится простым умножением их соответствующих элементов:
А◦В=(аijbij)= . (П.2.27)
. (П.2.27)
Произведение Кронекера
Если матрица А имеет размеры тхn и матрица В имеет размеры pхq, то их произведение Кронекера определяется матрицей размеров тpхnq
А B=
B= . (П.2.28)
. (П.2.28)
В общем случае, А B≠В
B≠В А и матрицы могут быть векторами [Seber (2008) cтр.234].
А и матрицы могут быть векторами [Seber (2008) cтр.234].





















