Приложение А Обозначения векторов и матриц
Приложение: Элементы матричной алгебры
В приложении рассматриваются элементы теории матриц, используемые в статистических методах. Приводятся доказательства только того, что представляется полезным. Другие доказательства можно найти в [Searle (1982), Harville (2008), Schott (2016), Беклемишев (2006)], а также в других книгах по теории матриц.
П.1. Обозначения векторов и матриц
Матрицы, векторы и скаляры
Если линейную модель (2.5.5) записать для каждого из n опытов эксперимента, то n полученных моделей можно представить системой уравнений
 . (П.1.1)
. (П.1.1)
Эту систему уравнений можно записать в компактном матричном виде
у=Xq+e,
где у= , X=
, X= , q =
, q = и e=
и e= . На основе данных эксперимента с помощью теории матриц можно оценить параметры этой модели и осуществить её статистическую проверку.
. На основе данных эксперимента с помощью теории матриц можно оценить параметры этой модели и осуществить её статистическую проверку.
Рекомендуемые материалы
Матрицей является прямоугольная или квадратная таблица чисел или переменных. Для обозначения матриц используются заглавные буквы жирным шрифтом. Все рассматриваемые здесь элементы матриц - действительные числа или переменные, значения которых - действительные числа. Для представления элементов матрицы А в виде переменных используются следующие обозначения:
А=(aij)= . (П.1.2)
. (П.1.2)
Первый подстрочный индекс i в обозначении aij указывает номер строки, а второй j – номер столбца. Обозначение А=(aij) представляет матрицу её типичным элементом.
Одно действительное число называется скаляром, то есть 2,5, –9 и 7,26 - скаляры. Переменная, имеющая скалярные значения, будет обозначаться строчной буквой, например, с.
Чтобы подчеркнуть, что матрица А имеет п строк и р столбцов, то есть имеет размеры пхр, иногда будем писать А=Апр. Матрицу А11=(а11) будем отождествлять со скалярным числом а11.
Вектор является матрицей, состоящей из одного столбца элементов. Элементы вектора могут иметь один подстрочный индекс, например,
х= .
.
Для обозначения вектора столбца используется строчная буква жирным шрифтом, например х, а для обозначения вектора строки используется строчная буква жирным шрифтом с подстрочным символом с, например хс. Вектор строка может быть получена транспонированием вектора столбца, например, хТ= [х1, х2, х3] = [x1 x2 x3], где Т - символ транспонирования. Для разделения элементов вектора используются запятые или пробелы.
Элементы вектора размеров рх1 могут рассматриваться как координаты конца геометрического вектора в пространстве р измерений, если начало этого вектора находится в начале координат.
Две матрицы или два вектора равны, если они одинаковых размеров и их элементы в соответствующих позициях равны, например,
 =
= , но
, но  ≠
≠ .
.
Транспонирование
Если в матрице А поменять по порядку местами строки и столбцы, то в результате получится транспонированная матрица обозначаемая АТ. Так, если А определяется A=(aij), то АТ определяется в виде
АТ=(aij)Т=(aji). (П.1.3)
Это обозначение указывает, что элемент в i-й строке и j-м столбце матрицы А находится в j-й строке и i-м столбце матрицы АТ. Если матрица А размеров pxn, то матрица АТ имеет размеры nxp.
Если матрица транспонируется два раза, то получается исходная матрица.
Теорема П.1. Если А - любая матрица, то
(АТ)Т=А. (П.1.4)
Доказательство: В силу (П.1.3), АТ=(aij)Т=(aji). Тогда (АТ)Т=(aji)Т=(aij)=А.
□
Матрицы специального вида
Если транспонированная матрица А является такой же, как и исходная матрица, то есть, если АТ=А или, что то же самое, (aji)=(aij), то матрица А является симметричной. Например, матрица
А=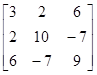
симметричная. Очевидно, что все симметричные матрицы квадратные.
Диагональ квадратной матрицы А=Арр состоит из элементов a11, a22, ..., aрр
А= .
.
Если матрица содержит нули во всех позициях за пределами диагонали, то это диагональная матрица. Например, диагональная матрица
D=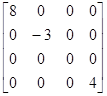
обозначаться также в виде
D=диаг(8, –3, 0, 4).
Диагональная матрица с диагональными элементами равными 1 называется единичной матрицей и обозначается I, например,
I= . (П.1.5)
. (П.1.5)
Верхняя треугольная матрица представляет собой квадратную матрицу с нулями ниже диагонали, например,
Т= .
.
Нижняя треугольная матрица является квадратной матрицей с нулями выше диагонали.
"4.1 Доарийский период - индская цивилизация" - тут тоже много полезного для Вас.
Вектор, все элементы которого равны 1, обозначим единицей жирным шрифтом:
1= . (П.1.6)
. (П.1.6)
Квадратную матрицу, все элементы которой равны 1, обозначим Е, например,
Е= . (П.1.7)
. (П.1.7)
И наконец, вектор нулей обозначим 0 и матрицу нулей обозначим O, например,
0= и О=
и О= . (П.1.8)
. (П.1.8)




















