Функциональные ряды

Функциональные ряды.

18.2.1. Основные определения. Пусть дана бесконечная последовательность функций .

независимой переменной х, имеющих общую область определения D. Ряд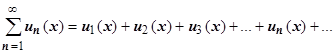

называется функциональным рядом.

            Примеры: 1. ;

2. ;

3. .

Для каждого значения  функциональный ряд превращается в числовой ряд, сходящийся или расходящийся. Так, первый из примеров - геометрическая прогрессия со знаменателем х, этот ряд сходится при х=1/2 и расходится при х=2.

Определение. Значение , при котором функциональный ряд сходится, называется точкой сходимости функционального ряда. Множество всех точек сходимости функционального ряда называется областью сходимости этого ряда. Область сходимости обозначим .

Рекомендуемые материалы

Так, для первого из приведённых примеров область сходимости - интервал (-1, 1); для второго - ряда Дирихле - область сходимости - полуось х>0; третий ряд абсолютно сходится в любой точке х, так как при любом х справедливо ; следовательно, область сходимости третьего ряда  ).

Для каждого  мы получаем сходящийся числовой ряд, свой для каждого х, поэтому сумма функционального ряда есть функция , определённая на области . Так, для первого примера, как мы знаем, , т.е.  на интервале

(-1, 1); вне этого интервала равенство не имеет места; так, в точке х=2 ряд расходится, а .  Сумма второго ряда - знаменитая функция Римана , определённая на полуоси ; эта функция играет важную роль в теории чисел. Сумма третьего ряда, как мы увидим дальше при изучении рядов Фурье, равна функции периода , получающаяся в результате периодического повторения функции , определённой на отрезке , по всей числовой оси.

            Коль скоро мы осознали, что сумма функционального ряда - функция, встаёт вопрос о свойствах этой функции. Так, члены ряда могут иметь свойства непрерывности, дифференцируемости, интегрируемости и т.д. Будет ли обладать этими свойствами сумма ряда? То, что это не праздный вопрос, показывает следующий пример. Пусть , , , , …, , …. Ряд  состоит из непрерывных членов, найдём его область сходимости и сумму. Частичная сумма ряда  . Последовательность  при  имеет конечный предел только, если  (это и есть область сходимости ряда), при этом  Таким образом, для ряда, члены которого - непрерывные функции, мы получили разрывную на области сходимости сумму.

Сумма ряда сохраняет хорошие свойства своих членов в том случае, если ряд сходится равномерно.

            18.2.2. Равномерная сходимость функционального ряда. Факт сходимости ряда  к своей сумме  в точке сходимости х означает, в соответствии с определением предела, то, что для любого числа  существует такое натуральное N, что при n>N  верно . Здесь  - частичная сумма ряда в точке х. Число N  зависит, естественно, от , но оно зависит и от х, т.е. . В некоторых точках области сходимости ряд может сходиться к своей сумме быстро, т.е. неравенство  будет выполняться при не очень больших значениях N, в других точках эта сходимость может быть медленной. Если ряд сходится к своей сумме примерно с одинаковой скоростью во всех точках х, то сходимость называется равномерной. Более точно, говорят, что ряд  сходится равномерно на области G, если для любого числа  существует такое натуральное число , одно и то же для всех точек ,что при n>N  выполняется неравенство  (или, что тоже самое, , где  - остаток ряда после n-го члена).

        

Понятие равномерной сходимости - одно из фундаментальных понятий функционального анализа. Именно равномерная сходимость обеспечивает сохранение суммой ряда хороших свойств своих членов. Чтобы осознать смысл и значение этого понятия, требуется время, которого у нас, к сожалению, нет. К счастью, имеется простой и понятный достаточный признак равномерной сходимости - признак Вейерштрасса.

            Признак Вейерштрасса. Если существует такой  положительный сходящийся числовой ряд , что члены функционального ряда  в любой точке  удовлетворяют неравенству , то функциональный ряд сходится равномерно в области G.

            Числовой ряд, удовлетворяющий неравенству , называется мажорирующим рядом, или мажорантой функционального ряда; про функциональный ряд говорят, что он мажорируется числовым рядом.

           

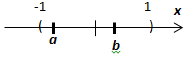
            Рассмотрим примеры, приведённые в начале раздела. Геометрическая прогрессия  равномерно сходится на любом отрезке , целиком лежащем в области сходимости (-1,1). Действительно, построим мажоранту для геометрической прогрессии на . Из чисел а, b выберем большее по модулю. Пусть, например, . Тогда для любого  выполняется . Таким образом, сходящийся (так как ) числовой ряд  мажорирует на  функциональный ряд , откуда, по признаку Вейерштрасса, следует равномерная сходимость этого функционального ряда.

            Ряд  равномерно сходится на любой полуоси , так как на этом множестве он мажорируется рядом .

            Ряд  равномерно сходится на всей числовой оси (мажоранта для этого ряда уже получена - это ряд ).

            18.2.3. Свойства равномерно сходящихся рядов.

            18.2.3.1. Теорема о непрерывности суммы равномерно сходящегося ряда непрерывных функций. Если члены функционального ряда  - непрерывные функции, и этот ряд равномерно сходится на отрезке , то сумма этого ряда непрерывна на .

            18.2.3.2. Теорема о почленном интегрировании равномерно сходящегося ряда. Пусть члены функционального ряда непрерывны на отрезке , и ряд равномерно сходится к своей сумме  на этом отрезке: . Тогда , т.е. интеграл от суммы ряда равен сумме ряда, составленного из интегралов от членов равномерно сходящегося ряда.

            18.2.3.3. Теорема о почленном дифференцировании равномерно сходящегося ряда. Пусть члены сходящегося ряда  - дифференцируемые на отрезке  функции, и ряд, составленный из производных , равномерно сходится на . Тогда ряд  можно почленно дифференцировать, и , т.е. производная суммы ряда равна сумме ряда из производных.

Отметим тонкость, заключённую в этой теореме: для того, чтобы ряд можно было почленно дифференцировать, требуется равномерная сходимость не самого этого ряда, а ряда, составленного из производных его членов. 

            Эти свойства равномерно сходящихся рядов по нашей программе принимаются без доказательства; мы будем ими пользоваться при изучении степенных рядов. Однако уже сейчас мы можем сделать из этих теорем тонкие и важные выводы. Ряд  - геометрическая прогрессия со знаменателем , поэтому его сумма равна : . Мы доказали, что этот ряд равномерно сходится на любом отрезке , целиком лежащем в области сходимости (-1,1), поэтому его можно почленно проинтегрировать в пределах от 0 до : . Вычисляя интегралы, получаем  . Это не только неожиданное и красивое представление числа  в виде ряда , но и удобный способ его вычисления с любой точностью с простой оценкой остатка по первому отброшенному члену, так как получен ряд Лейбницевского типа (см. раздел 18.1.4.2).

Степенные ряды.

            18.2.4.1. Определение. Степенным рядом называется функциональный ряд вида ,

где  - постоянные (коэффициенты ряда),  - фиксированное число (центр сходимости). Степенной ряд имеет по меньшей мере одну точку сходимости - точку .

            Все содержательные сведения о степенном ряде содержатся в теореме Абеля.

            18.2.4.2. Теорема Абеля. Если степенной ряд сходится в точке , то

1. он абсолютно сходится в любой точке х, удовлетворяющей неравенству  (т.е. находящейся ближе к точке , чем );

2. он сходится равномерно на любом отрезке , целиком лежащем на интервале  (т.е. на интервале с центром в  радиуса ).

3. Если этот ряд расходится в точке , то он расходится в любой точке х, удовлетворяющей неравенству  (т.е. находящейся дальше от точки , чем ).

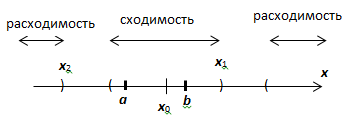
            Доказательство. 1. Из сходимости ряда  в точке  следует, что его общий член  стремится к нулю при ; любая последовательность, имеющая предел, ограничена, следовательно, существует число С такое, что . Пусть точка х удовлетворяет неравенству , тогда . Оценим член ряда в точке х:

. Члены ряда в точке х по абсолютной величине не превосходят членов сходящейся геометрической прогрессии, следовательно, ряд сходится абсолютно в точке х, следовательно, он сходится абсолютно в любой точке интервала .

             2. Пусть отрезок , целиком лежит на интервале . Из точек а, b выберем ту, которая находится дальше от точки , примем для определённости, что это - точка а: . Тогда для любого х из этого отрезка . В точке  ряд , по доказанному, сходится абсолютно, но он является на  мажорантой для ряда , следовательно, степенной ряд сходится равномерно на отрезке .

            3. Пусть степенной ряд расходится в точке , и . То, что ряд расходится в точке х, докажем от противного. Если предположить, что он сходится в точке х, то, по доказанному, он сходится во всех точках, расположенных ближе к , чем х, следовательно, он сходится в точке , что противоречит условию.

       

18.2.4.3. Радиус сходимости, интервал сходимости и область сходимости степенного ряда. Из теоремы Абеля следует, что существует такое число R  (возможно, ) такое, что при  степенной ряд сходится, при  ряд расходится. Действительно, пусть в точке  ряд сходится, в точке  ряд расходится. Рассмотрим точку , расположенную между областями, в которых установлена сходимость и расходимость. В точке  числовой ряд  либо сходится, либо расходится. Если он сходится, то мы можем перенести точку  в точку ; если ряд в точке  расходится, мы переносим в  точку . Продолжая этот процесс, мы сблизим точки  и , эта граница и определит число R.

            Определение. Число R  такое, что при  степенной ряд сходится, при  ряд расходится, называется радиусом сходимости. Интервал  называется интервалом сходимости степенного ряда.

            Сходимость ряда в концевых точках интервала сходимости должна исследоваться отдельно. В  зависимости от поведения ряда на концах интервала сходимости область сходимости степенного ряда может быть одной из следующих: , , , .

            Итак, для определения области сходимости степенного ряда надо найти его интервал сходимости R, затем исследовать поведения ряда в концевых  точках интервала сходимости .

Свойства степенного ряда и его суммы.

1. Почленное интегрирование или дифференцирование степенного ряда не меняют его радиус сходимости.

            Доказательство. Под почленным интегрированием понимается интегрирование ряда  по отрезку . Результат этой операции: .

Это тоже степенной ряд, его радиус сходимости  равен радиусу сходимости исходного ряда.

            Ряд, получающийся в результате почленного дифференцирования тоже степенной ряд: . Его радиус сходимости  тоже равен радиусу сходимости исходного ряда.

            2. (Почленное интегрирование степенного ряда). Пусть сумма степенного ряда на области сходимости равна функции , т.е. . Тогда для  .

            Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда на отрезке  и Теоремы 18.2.3.2 о почленном интегрировании равномерно сходящегося ряда.

3. (Почленное дифференцирование степенного ряда). Степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и .

            Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда, составленного из производных членов исходного ряда, на любом отрезке, лежащем в интервале сходимости   и Теоремы 18.2.3.3 о почленном дифференцировании равномерно сходящегося ряда.

4. (Бесконечная дифференцируемость суммы степенного ряда). Сумма  степенного ряда в любой точке интервала сходимости имеет производные любого порядка; эти производные могут быть получены последовательным почленным дифференцированием исходного ряда.

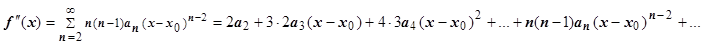
Доказательство. Справедливость этого утверждения следует из доказанной теоремы о почленном дифференцировании степенного ряда; последовательное применение этой теоремы даёт   и т.д.

18.2.5. Ряд Тейлора. Мы доказали, что сумма  степенного ряда в любой точке интервала сходимости бесконечно дифференцируема. Выразим коэффициенты ряда через производные суммы (похожую задачу мы решали в разделе 7.7. Формула Тейлора).

. Положим здесь . Все члены ряда, кроме нулевого, исчезают, и .

. Положим  , тогда .

. .

. .

Продолжая этот процесс, получим . Заменив коэффициенты полученными выражениями, представим ряд как

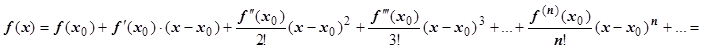
. Ряд, стоящий в правой части этой формулы, называется рядом Тейлора функции . В частном случае, когда  и ряд принимает вид

, его принято называть рядом Маклорена. Напомним, что эти ряды получены в предположении, что  - сумма степенного ряда и х - точка интервала сходимости.

           

            Теперь рассмотрим обратную задачу: какой должна быть функция , чтобы её можно было представить в виде суммы степенного ряда? Первое, что очевидно, это то, что  должна быть бесконечно дифференцируемой функцией (так как сумма ряда          бесконечно дифференцируема). Второе - то, что коэффициенты ряда должны быть равны . Поэтому предположим, что дана бесконечно дифференцируемая функция , мы нашли коэффициенты ряда по формуле , составили формальный ряд  и нашли область его сходимости. Будет ли сумма этого ряда на области сходимости равна ? Это тот вопрос, которым мы будем заниматься дальше.

            Приведём пример, когда ряд Маклорена функции  сходится не к , а к другой функции. Пусть  Мы докажем, что все производные этой функции в точке х=0 равны нулю. При  . . Такие неопределённости придётся раскрывать при вычислении любой производной; заменой t=1/x они сводятся к неопределённостям, содержащим степенные и показательные функции, значение предела во всех случаях определяется пределом показательной функции и равно нулю. Значение производной в точке х=0 находим по определению производной:

. Итак, производная  непрерывна в точке х=0 и равна нулю.  и т.д. Так доказывается, что все производные в точке х=0 равны нулю. Как следствие, все коэффициенты ряда Тейлора этой функции равны нулю, и на всей числовой оси ряд сходится к функции, тождественно равной нулю, а не к .

            Сформулируем условия, при которых ряд Тейлора функции  сходится к этой функции. Эти условия удобно сформулировать в терминах остаточного члена формулы Тейлора. Напомним результаты раздела 7.7. Формула Тейлора: если  имеет в окрестности точки  все производные до n+1-го порядка включительно, то  может быть представлена в виде формулы Тейлора с остаточным членом в форме Лагранжа: , где  - остаточный член в форме Лагранжа;  - точка, расположенная между х и , .

            Теорема. Для того, чтобы бесконечно дифференцируемая функция  в окрестности точки  разлагалась в ряд Тейлора, необходимо и достаточно, чтобы .

            Доказательство. Необходимость. Пусть в окрестности точки  функция  представлена в виде сходящегося к этой функции ряда Тейлора 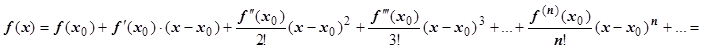, где  - частичная сумма ряда,  - его остаток. Так как  имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа: . Сравнивая эти представления, получаем . Из сходимости ряда к  следует, что , что и требовалось доказать.

            Достаточность. Если , то , т.е. остаток ряда стремится к нулю при , т.е. ряд сходится к функции .

. Применения степенных рядов.

18.2.6.3.1. Приближённое вычисление значений функций. Идея таких вычислений простая. Пусть известно значение функции в точке , и функция разлагается в окрестности точки  в ряд Тейлора. Тогда значение функции в точке , которое надо найти, равно , и принимается . Естественно, мы должны гарантировать, что погрешность такого приближения не превышает заданной величины . Погрешность равна остатку ряда после n-го члена (или остаточному члену формулы Тейлора), поэтому необходимо строить оценку сверху для  (или ). При оценке  принципиально отличны два случая. Если остаток - знакочередующийся ряд, то  просто оценивается по своему первому члену. Если остаток не является знакочередующимся рядом, то необходимо оценивать всю его сумму. Обычно в этом случае остаток мажорируют сходящейся геометрической прогрессией. В разделе 18.4.2. Знакочередующиеся ряды мы рассмотрели и тот, и другой случай при нахождении значений  и ; в разделе 7.9.2. Приближённые вычисления с помощью формулы Тейлора приведён пример вычисления значения  с погрешностью . Другие примеры будут рассмотрены ниже.

18.2.6.3.2. Интегрирование функций.

1. Как мы знаем, интеграл  аналитически не берётся. Это специальная функция, называемая интегральным синусом и обозначаемая . Получим разложение этой функции в степенной ряд. , ,  почленно интегрируем: .  Ряд сходится к  при . Теперь легко вычислить значение этой функции в любой точке. Пусть, например, надо найти  с погрешностью . . Ряд знакочередующийся, первый член, меньший , третий, поэтому .

            2. Найти . Этот интеграл берётся аналитически. Надо разложить знаменатель на множители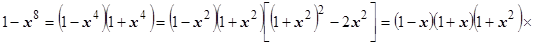

2 Свойства определённого интеграла - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

, разложить подынтегральную функцию на пять простых дробей, найти восемь неопределённых коэффициентов и т.д., и после этого вычислять значение первообразной в начальной и конечной точках. Поступим по другому. Разложим подынтегральную функцию в ряд Маклорена и почленно проинтегрируем: , . Остаток ряда после n-го члена  . Если , достаточно взять n=2, и .

18.2.6.3.3. Интегрирование дифференциальных уравнений с помощью степенных рядов. Пусть дана задача Коши: ,

                                    

Решение этой задачи в виде ряда Тейлора ищется так.  . Первые n коэффициентов ряда известны из начальных условий, остальные находятся последовательным дифференцированием уравнения.

            Примеры. 1. . Из уравнения находим . Дифференцируем уравнение: . Далее дифференцируем уравнение и находим значение производной в точке : , . Так мы можем вычислить производные любого порядка. Решение задачи Коши: .

            2. . Находим:     Закономерность понятна. Производные порядка 3n-1 и 3n равны нулю, производная порядка 3n+1 равна , поэтому  С помощью признака Даламбера легко убедится, что этот ряд сходится при , следовательно, даёт решение задачи Коши на всей числовой оси.