Метод простых итераций для решения систем линейных алгебраических уравнений
Метод простых итераций для решения систем линейных алгебраических уравнений.
Рассмотрим решение этой системы методом простых итераций. Для применения этого метода необходимо предварительно преобразовать систему (12) к виду
 , (13)
, (13)
где матрица  такова, что выполнены достаточные условия сходимости итерационного процесса :
такова, что выполнены достаточные условия сходимости итерационного процесса :  или
или  .
.
Зададим произвольно начальный вектор приближения  и подставим его в правую часть преобразованной системы уравнений. Получим первое приближение
и подставим его в правую часть преобразованной системы уравнений. Получим первое приближение  . Аналогично получим
. Аналогично получим  . Итак, итерационная формула
. Итак, итерационная формула
 (14)
(14)
или в координатной форме:
 (15)
(15)
осуществляет итерации по “совокупности координат”. Последовательность векторов  , полученных по этой формуле, сходится к решению, если выполнены вышеприведенные достаточные условия сходимости.
, полученных по этой формуле, сходится к решению, если выполнены вышеприведенные достаточные условия сходимости.
Рекомендуемые материалы
Пусть  , тогда, переходя к пределу в равенстве (14), имеем
, тогда, переходя к пределу в равенстве (14), имеем
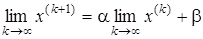
или имеет место формула (13). Следовательно, вектор  - решение системы.
- решение системы.
Если в исходной системе (12) преобладание диагональных элементов  над остальными коэффициентами значительное, то сходимость итерационного процесса обеспечена. В этом случае переход от исходной системы (12) к виду (13) можно осуществить путем деления каждого уравнения системы (12) на коэффициент
над остальными коэффициентами значительное, то сходимость итерационного процесса обеспечена. В этом случае переход от исходной системы (12) к виду (13) можно осуществить путем деления каждого уравнения системы (12) на коэффициент  , формирования столбца
, формирования столбца  в левой части и переноса остальных членов в правую часть. Введем обозначения
в левой части и переноса остальных членов в правую часть. Введем обозначения  . Тогда
. Тогда
Вместе с этой лекцией читают "В чем разница между конфуциоцами и легистами".
 .
.
Рабочая формула итерационного процесса имеет в этом случае следующий вид:
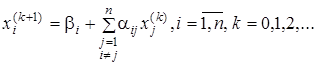
Начальное приближенное решение можно взять произвольно, например, равным столбцу свободных членов  . Далее последовательно получаются приближения
. Далее последовательно получаются приближения  . Если для преобразованной системы (13) выполнено по меньшей мере одно из достаточных условий сходимости, то процесс итераций (14) сходится к единственному решению этой системы, независимо от выбора начального приближения.
. Если для преобразованной системы (13) выполнено по меньшей мере одно из достаточных условий сходимости, то процесс итераций (14) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Для системы (12) метод итераций сходится, если выполнены неравенства  , т.е. модули диагональных коэффициентов в каждом уравнении больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
, т.е. модули диагональных коэффициентов в каждом уравнении больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
Итерационный процесс следует закончить, когда два последовательных приближения близки между собой по норме  , где
, где  - заданная точность.
- заданная точность.





















