Газодинамические функции потока
Газодинамические функции потока
1.1. Полная энтальпия потока.
Из термодинамики известна связь между теплоемкостями:
 ;
; 
Теплосодержание или энтальпия:
 или
или 
Тогда:
 →
→  , или
, или 
Принимая во внимание что:  , можно записать:
, можно записать:
Рекомендуемые материалы
 (1)
(1)
Уравнение энергии:

С учётом (1) можно представить:


В случае энергетически изолированного течения:
 , или:
, или:

Из последнего уравнения видно, что если газовую струю затормозить полностью, то теплосодержание газа достигает максимально возможного значения:
 – полное теплосодержание.
– полное теплосодержание.
1.2. Соответствующая полному теплосодержанию температура  называется температурой торможения.
называется температурой торможения.

Для воздуха  .
.
Истинная температура обтекаемой газом поверхности отличается от температуры торможения за счёт теплоизлучения в пространство:
 ,
,
где φ – коэффициент торможения.
При замере температуры газа, движущегося с большой скоростью, термометром:


1.3. Максимальная скорость потока. Число Маха.
Из уравнения полного теплосодержания  следует, что максимальная скорость потока получится в том случае, когда:
следует, что максимальная скорость потока получится в том случае, когда:

Число Маха характеризует степень преобразования энтальпии в кинетическую энергию потока.
· При М<1 – течение газа называется дозвуковым;
· При М>1 – сверхзвуковым;
· При М=1 – режим критический и температура – критическая.
 ;
; 
 ;
; 

Отношение скорости потока к критической скорости звука под коэффициент скорости, так же как и М характеризует степень энтальпии потока в кинетическую энергию.
Данному числу Маха М соответствуем вполне определимые значения  .
.
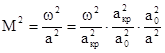

1.4. Механическая форма уравнения энергии.
Уравнение энергии для единицы массы газа при отсутствии теплообмена с окружающей средой в дифференциальной форме:
 – механическая форма уравнения энергии.
– механическая форма уравнения энергии.

После интегрирования:
 – обобщенное уравнение Бернулли
– обобщенное уравнение Бернулли
Рекомендация для Вас - Абылай Хан.
Если  и
и  , то:
, то:
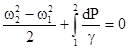
Для несжимаемой жидкости, когда γ=const:
 , или:
, или:























