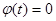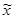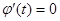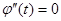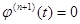Погрешность интерполяционного многочлена Лагранжа
2020-06-032021-03-09zzyxelСтудИзба
Погрешность интерполяционного многочлена Лагранжа
Пусть f(x) — непрерывная, имеющая непрерывные производные до (n+1) порядка.
Ln(x) — многочлен Лагранжа: Ln(xi)=f(xi) для всех i=0,...,n.
[a,b] — отрезок, содержащий узлы x0, x1, ..., xn.
Найдем оценку отличия значения f(x) от значения Ln(x) в точке 
, не совпадающей ни с одним из узлов.
Запишем равенство
, где 
.
Рассмотрим функцию
.
Рекомендуемые материалыFREE Бараненков Г. С., Демидович Б. П., Ефименко В. А. - Задачи и упражнения по математическому анализу для втузов - 2004 -61% Решение 4 билетов из РК-1 FREE рк тфкп модуль 1 иу4 примеры билетов РК1 Для СМ 14 Вариант "Кратные Интегралы ФН-2" FREE Решенные задачки из Демидовича по рядам Раабе 2598-2604 FREE Домрина. Лекции (2009) v4.0
| если t= x0, x1, ..., xn, | всего (n+2) точки | по т. Роля, если ф-ия в двух точках равна 0, то существует точка, в которой производная обращается в 0 |
|
| (n+1) точка на [a,b] | ||
|
| n точек на [a,b] | ||
| ... | |||
|
| 1 точка на [a,b] | ||
Рекомендуем посмотреть лекцию "14 Ряды Тейлора и Маклорена".
Т.е. существует 
: 
.
Т.к. 
, и 
, получаем
, следовательно 
.
Þ 
.
.
.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
