Системы нелинейных уравнений - метод простых итераций

Системы нелинейных уравнений: метод простых итераций

Задача: Дано:    (7),

где  – столбец неизвестных,  – столбец, состоящий из скалярных функций от n переменных.

Метод простых итераций:

1) Преобразовать уравнение (7) в уравнение вида   (8) ;

2) Составить рекуррентную формулу:  (9);

3) Выбрать любое начальное приближение . По формуле (9) найти , , …, ;

4) Если норма разности  уменьшается, то метод сходится, и последнее найденное приближение  приблизительно равно решению системы (7).

Опр. Метрическое пространство H — множество, на котором задана функция метрики (расстояния) r(a,b), удовлетворяющая условиям:

Рекомендуемые материалы

1) r(a,b) ³ 0, и r(a,b) = 0 Û a = b;

2) r(a,b)  = r(b,a);

3) r(a,b) + r(b,c) ³ r(a,c).

В нашем случае H = úⁿ, .

Опр. Отображением в метрическом пространстве называется функция

g : H ® H.

Опр. Отображение называется сжимающим, если существует число q:

0 ≤ q < 1, такое, что для любых x₁, x₂ Î H выполняется

r(g(x₁),g(x₂)) ≤ q×r(x₁, x₂).

Теорема.

Если отображение  является сжимающим, то уравнение  имеет единственное решение  и .

Док-во:

1. Поскольку  является сжимающим, то

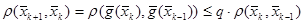
   (обозначили ).

Тогда для l > k выполняется

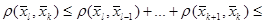
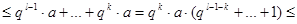
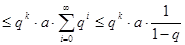
Т.о. при l ® ¥,  k ® ¥ выполняется , следовательно последовательность , , …, ,… сходится к предельному значению .

2.

.

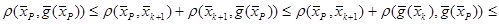
Это неравенство верно для любого k, т.е.  меньше сколь угодно маленького положительного числа, т.е. .

Следовательно,  — точное решение уравнения (8).

3. Предположим, что уравнение (8) имеет два точных решения  и .

.

 .

Теорема доказана.

Частный случай. Пусть n = 1, т.е. система состоит из одного уравнения 

f(x) = 0 с одной неизвестной x.

Уравнению равносильно x = g(x). Решение x_T — точка пересечения графиков функций y = x и y = g(x).

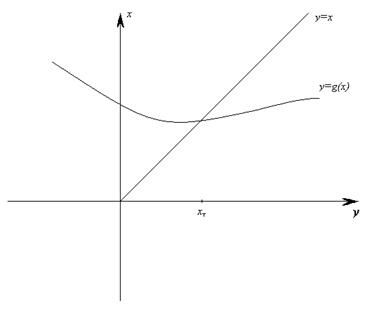
x₁ = g(x₀),    x₂ = g(x₁), …

Если Вам понравилась эта лекция, то понравится и эта - 9. Организация как функция менеджмента.

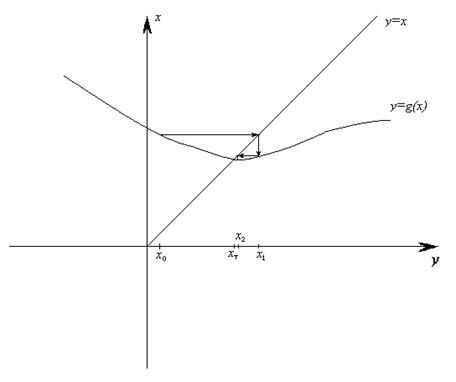
На этом рисунке метод простых итераций сходится.

На следующем — нет.

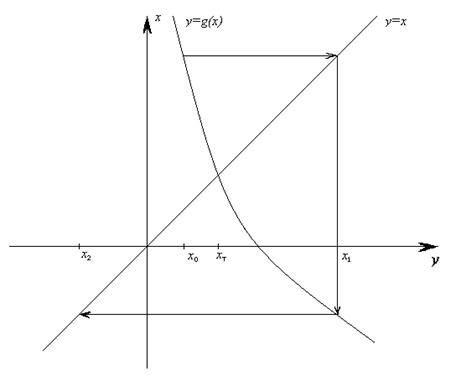
Аналогом метода Зейделя является способ, когда координаты нового приближения  вычисляются по очереди из одного уравнения системы:

.