Градиент
Градиент
В этом параграфе мы обсудим специально производную числовой функции векторного аргумента, т.е. функции вида (1) (введение к гл. 2) при  .
.
Из предыдущих рассмотрений ясно, что матрица Якоби такой функции является матрицей-строкой, в каждой точке  , в которой функция дифференцируема, имеющую вид:
, в которой функция дифференцируема, имеющую вид:
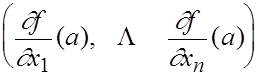
Введем вектор, имеющий в соответствующем ортонорме пространства  вид
вид

Этот вектор называется градиентом функции  в точке
в точке  и обозначается
и обозначается  (или
(или  ).
).
Тогда равенство (1) из п. 2.4 (с учетом условия (2) того же параграфа) перепишется в виде:
Рекомендуемые материалы
 , (1)
, (1)
где  . Мы можем теперь написать вместо вектора
. Мы можем теперь написать вместо вектора  просто бесконечно малую по сравнению с нормой вектора
просто бесконечно малую по сравнению с нормой вектора  , так как сама функция и ее приращение являются скалярами.
, так как сама функция и ее приращение являются скалярами.
Стоящая в равенстве (1) линейная форма называется первым дифференциалом функции  в точке
в точке  и обозначается
и обозначается  .
.
Итак,
 (2)
(2)
и
 (3)
(3)
С использованием вектора градиента мы можем переписать (3) в виде:
 (4)
(4)
Таким образом, первый дифференциал функции в точке равен скалярному произведению вектора градиента в этой точке на вектор приращения аргумента.
Необходимо подчеркнуть следующее. Как только в точке определены все частные производные функции, так мы можем формально вычислить вектор, компоненты которого равны соответственно частным производным в точке, а затем вычислить и скалярное произведение этого вектора на вектор приращения аргумента. Эти вычисления, однако, будут иметь смысл и дадут градиент функции в точке и первый дифференциал функции в точке, только если функция в этой точке будет дифференцируема, т.е. если разность между приращением функции в точке и значением произведения  будет бесконечно малой высшего порядка по сравнению с нормой приращения аргумента.
будет бесконечно малой высшего порядка по сравнению с нормой приращения аргумента.
Так для функции

обе частные производные в точке  существуют и равны нулю, но функция в точке не будет даже непрерывна (как мы убедились в п. 2.3). Следовательно, в этой точке данная функция не будет иметь ни градиента, ни первого дифференциала.
существуют и равны нулю, но функция в точке не будет даже непрерывна (как мы убедились в п. 2.3). Следовательно, в этой точке данная функция не будет иметь ни градиента, ни первого дифференциала.
Подобное же замечание справедливо и в общем случае векторной функции векторного аргумента: формальная возможность вычислить матрицу частных производных в точке еще не означает, что это будет матрица оператора производной в данной точке.
Обратим внимание на то, что первый дифференциал есть функция точки, т.е. для переменной точки  (в которой функция
(в которой функция  дифференцируема, функция первого дифференциала есть
дифференцируема, функция первого дифференциала есть
 .
.
Обсудим теперь связь между понятиями градиента и производной по направлению.
Как известно, в общем случае производная по направлению функции  в точке
в точке  равна результату действия линейного оператора производной
равна результату действия линейного оператора производной  в точке на единичный вектор направления :
в точке на единичный вектор направления :
(5)
(см. формулу (4) п. 2.4).
Для числовой функции  выражение (5) примет вид:
выражение (5) примет вид:
 (6)
(6)
Итак, производная по направлению в точке равна скалярному произведению градиента в данной точке на единичный вектор направления.
Следовательно, если вектор направления коллинеарен вектору градиента, то производная по направлению имеет максимальное значение, равное норме градиента:
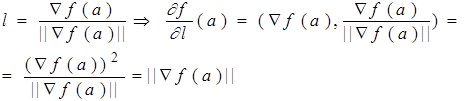
Содержательно это означает, что направление градиента есть направление наибыстрейшего возрастания функции.
Точно также направление, задаваемое вектором, противоположным вектору градиента (и называемому вектором антиградиента), есть направление наибыстрейшего убывания функции (в рассматриваемой точке).
В трехмерном пространстве единичный вектор направления задается своими проекциями на оси координат, которые равны косинусам углов, образуемых вектором направления с ортами осей (так называемые направляющие косинусы). В этом случае производная по направлению, задаваемому косинусами  , в некоторой точке с координатами
, в некоторой точке с координатами  будет равна:
будет равна:

В двумерном случае эта формула принимает совсем простой вид:
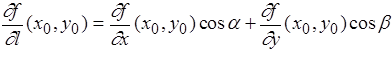
Опять-таки подчеркнем, что существование частных производных в точке не есть достаточное условие существования в этой точке производной по заданному направлению (отличному от базисного), хотя формально указанное выше скалярное произведение можно вычислить.
Так функция двух переменных, равная нулю на осях координат и единице во всех остальных точках плоскости, не дифференцируема в начале координат ни по одному направлению, кроме базисных, хотя и имеет в этой точке обе частные производные, равные нулю.
Бесплатная лекция: "Лабораторная работа Б" также доступна.
Замечание. Читатель, проработавший п. 1.12, поймет, что оператор производной числовой функции
производной числовой функции  в точке
в точке  , является линейным функционалом (или ковектором). Но, как следует из теоремы 1.8, для любого линейного функционала
, является линейным функционалом (или ковектором). Но, как следует из теоремы 1.8, для любого линейного функционала  , определенного на евклидовом пространстве, однозначно определен вектор
, определенного на евклидовом пространстве, однозначно определен вектор  , такой, что для любого
, такой, что для любого  . Понятно тогда, что вектор градиента функции в точке и есть этот самый вектор
. Понятно тогда, что вектор градиента функции в точке и есть этот самый вектор  для функционала производной в точке. Производная функция числовой функции векторного аргумента есть, очевидно, отображение
для функционала производной в точке. Производная функция числовой функции векторного аргумента есть, очевидно, отображение  пространства
пространства  в сопряженное пространство
в сопряженное пространство  .
.
Читатель без труда докажет, что градиент имеет следующие свойства:
1)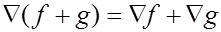
2)  (для любого вещественного
(для любого вещественного  )
)
3)  (градиент константы равен нулю).
(градиент константы равен нулю).
Аналогичные свойства имеет и первый дифференциал.






















