Оценки моментов решений стохастических уравнений. Непрерывность траекторий решений стохастических уравнений

§6. Оценки моментов решений стохастических уравнений. Непрерывность траекторий решений стохастических уравнений.

6.1. Теорема 13. 1) Пусть выполнены условия теоремы 12 и . Тогда существует положительная константа  такая, что

.

2) Пусть выполнены условия теоремы 12 и  , то существует константа К такая, что

.

Доказательство. 1) Обозначим

,   .

 Применим формулу Ито к, имеем

Рекомендуемые материалы

             (32)

Так как  для любого, имеем из (32)

(33)
Из определений  и  следует, что ,

 поэтому из (33) имеем                                                          (31)

 Для оценки  и  воспользуемся неравенством Юнга ,  где , , . Рассмотрим  и положим , а . Из неравенства Юнга следует Р-п. н. для любого s

.

Рассмотрим  и положим , , имеем Р-п. н. для любого s

.

Поэтому неравенство (34) можно усилить, учитывая, что для каждого т существует константа  такая, что

 .           (35)

Последнее неравенство (35) можно усилить, учитывая, что: а) ,

б) так как для , то существует константа  такая, что

.

Отсюда в силу леммы Гронуолла-Беллмана, применённой к функции , имеем из (35)

.

В силу леммы Фату, из последнего неравенства, имеем

.

Первое утверждение теоремы доказано.

2) Оценим сверху, имеем в силу неравенства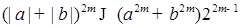

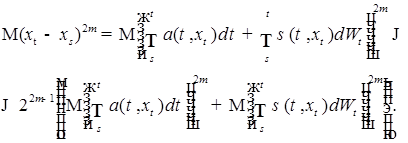
Отсюда, в силу неравенства Гёльдера и свойств стохастических интегралов, имеем

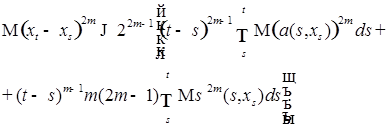
В силу замечания к теореме 12 имеем Р-п. н. для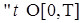

.

Поэтому последнее неравенство можно усилить

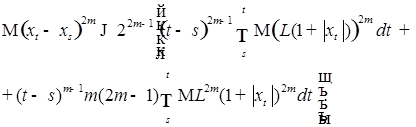
Значит существует константа  такая, что

11 - Специализированные процессоры для ИС - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

.

Воспользуемся теперь оценкой пункта 1 теоремы, в результате получим второе утверждение теоремы. Доказательство закончено.

6.2. Основываясь на втором утверждении теоремы легко установить утверждение.

Теорема 14. Пусть выполнены условия теоремы 13 и . Тогда решение стохастического уравнения (22) является непрерывным процессом.

Доказательство этого утверждения следует из пункта 2 теоремы 13 при , которое позволяет воспользоваться теоремой 2 главы 3.