Свойства компенсаторов точечных процессов. Случайная замена времени

§8 Свойства компенсаторов точечных процессов. Случайная замена времени.

8.1. Теорема 31. Справедливы утверждения.

1) Компенсатор  точечного процесса  допускает един­ственное разложение , где -  непрерывная составляющая, - разрывная составляющая.

2) Р -  п. н.

3) P – п. н. для любого t.

Доказательство. 1) Первое утверждение теоремы следует из теоремы 24.

2) Так как, то . Заметим, что - измерим, поэтому. Так как, то  Р - п. н.

3) Сначала заметим, что Р – п. н.

Рекомендуемые материалы

.

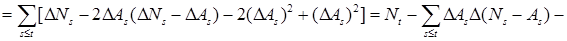
Люди также интересуются этой лекцией: 5.5 Греческая литература.

Так как является мартингалом, a  - предсказуемый возрастающий процесс. Поэтому из теоремы Дуба - Мейера следует третье утверждение. Теорема доказана.

8.2. Пусть - точечный процесс, а  - его компенсатор, где - измеримая функция.

Теорема 32. Пусть Р - п. н.  . Пусть существует функция

, обозначаемая через , такая, что. Тогда  - стандартный пуассоновский процесс (т. е. интенсивность его равна единице).

Доказательство. Сначала покажем, что процесс  имеет компенсатор t, т. е.  - мартингал относительно потока  и меры Р. Пусть - ограниченный предсказуемый процесс, тогда имеем, в силу теоремы 30, .

Покажем теперь, что . Очевидно, что - точечный процесс, поэтому . Отсюда следует, что . Значит . Доказательство закончено.