Марковские моменты. Локальные полумартингалы
§ 4 Марковские моменты. Локальные полумартингалы.
4.1. Определение. Отображение 
называется марковским моментом, если
для 
.
Конечный марковский момент (Р(
)=1) называется моментом остановки.
Обозначим 
для всех 
}.
Предложение 11. 
алгебра.
Доказательство. Очевидно, что: i) 
; ii) 
замкнута относительно операции взятия счетных пересечений; iii) если 
и 
, то 
и следовательно 
. Стало быть, алгебра.
Примеры: 1) 
.
2) Пусть 
- случайная последовательность, а 
-марковский момент. Определим 
, где 
Тогда 
измерима. (Докажите самостоятельно).
Рекомендуемые материалы
3) Пусть 
марковский момент. Действительно
.
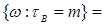
Предложение 10. Пусть 
марковский момент. Тогда 1) 
, 2)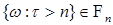 
Доказательство. 1) Очевидно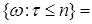 
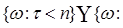
. Поэтому из определения марковского момента следует, что 
. Второе утверждение очевидно.
4.2. Пусть 
марковский момент относительно фильтрации 
.
Предложение 12. 1) Если t, s - марковские моменты, то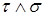 
min(t,s),
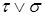
max(s,t), t+s, (t-s)+ 
max(t-s,0) являются марковскими моментами.
2) Если 
- марковские моменты и 
Р - п. н., то 
.
3) Если - марковские моменты, то 
принадлежат 
и
.
4) Если 
- последовательность марковских моментов. Тогда 
tn , 
tn , 
tn , 
tn , 
tn также являются марковскими моментами.
Докажите предложение 12 самостоятельно.
4.3. Определение. Последовательность 
называется остановленной, если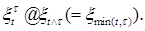 
Определение. Последовательность марковских моментов называется t-локализующей, если она неубывающая и Р - п. н. существует t =
tn . Если 
¥, то называется локализующей.
4.4. Определение. Последовательность 
называется локальным полумартингалом, если существует локализующая последовательность , такая, что остановленная последовательность 
является полумартингалом.
Определение. Последовательность 
называется мартингал-разностью, если существует М(xt | 
) для любого 
и М(
)=0 Р - п. н.
Из этого определения следует утверждение.
Предложение 13. Последовательность 
, где 
является мартингалом (относительно меры Р) тогда и только тогда, когда 
является мартингал разностью.
4.5. Лемма 14. Пусть - локальный мартингал с 
и 
либо 
. Тогда - мартингал.
Доказательство. Сначала покажем, что если выполнено , то и следовательно 
, для 
. Действительно. Пусть 
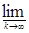
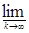- локализующая последовательность, тогда в силу леммы Фату имеем
М
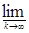= М
£ М = 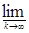М[
+ 
] = 
+ М
£ || + 
< ¥. Поэтому 
.
Заметим, что: а) |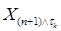
| £ 
; б) M<¥. Из того, что - локальный мартингал, следует М(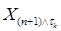
|
)= Р - п. н.. Воспользуемся теперь теоремой Лебега (о мажорируемой сходимости), в последнем равенстве имеем 
Р - п.н..
Доказательство закончено.
Следствие 15. Всякий локальный мартингал ограниченный сверху (снизу) является мартингалом.
"Базис" - тут тоже много полезного для Вас.
Теорема 16. Пусть - локальный мартингал (относительно меры Р). Тогда последовательность является супермартингалом (относительно меры Р).
Доказательство. В силу условий существует локализующая последовательность марковских моментов такая, что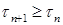 
P - п. н., причем 
Р - п. н. Поэтому в силу леммы Фату, имеем P - п. н.
= 
= 
³ M(
| 
) =
= 
.
Доказательство закончено.
