Мартингалы, супермартингалы, субмартингалы

§ 3 Мартингалы, супермартингалы, субмартингалы.

3.1. Пусть (,,,Р) – стохастический базис, последовательность { - согласована с потоком , и принимает значения в .

Определение. Последовательность (,)_t>1 называется мартингалом, если:
1) , 2)

Если выполнено 1) и  Р -п. н., то последовательность (,)_t>0 называется супермартингалом.

 Если выполнено 1) и  Р - п. н., то последовательность (,)_t>0 называется субмартингалом.

Пример. Пусть , где  независимые в совокупности случайные величины. Пусть , . Ясно, что

=

=++  +.

Отсюда следует, что:

Рекомендуемые материалы

а) (,)_t>1- мартингал, если для любого t;

б) (,)_t>1- супермартингал, если для любого t;

в) (,)_t>1- субмартингал, если для любого t;

Утверждение 5. Если (,)_t>0– марковская случайная последовательность с переходной вероятностью P(s,,t,B), то
P(s, t,B) – мартингал для , относительно потока алгебр  и меры Р.

Доказательство. Из соотношения Чепмена – Колмогорова имеем
Р-п. н. при :

M(P(u, ,t,B)|)=M(P(u, ,t,B)| ) = .

3.2. Теорема 6 (Дуба). Пусть (,)_t>0 – неотрицательный супермартингал, тогда с вероятностью 1 существует .

Замечания. 1) Покажем, что предложения о неотрицательности супермартингала (,)_t>0 можно отказаться. Очевидно, что ММ, т.е. в среднем последовательность - убывает. Пусть   Образуем новую последовательность . Понятно, что .Тогда , значит любой супермартингал представим в виде разности двух неотрицательных супермартингалов.

2) Если  - супермартингал, то  - субмартингал. Поэтому утверждение теоремы 6 верно и для субмартингалов.

3.2.1 Доказательство теоремы Дуба опирается на две вспомогательные леммы.

Пусть  числовая последовательность, a<b, [a,b] – отрезок. Обозначим  - число пересечений отрезка [a,b] последовательностью  снизу вверх.

Лемма 7 (О числе пересечений отрезка [a,b] снизу вверх).

Справедливо неравенство:

,

где

Доказательство. Обозначим

,         ,

,        ,

,    

Очевидно, что

Отсюда следует, что

(b-a) =.

Докзательство закончено.

Лемма 8. (О среднем числе пересечений). Пусть (,)_t>0– неотрицательный супермартингал, тогда М.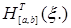

Доказательство.  В силу леммы 7 имеем неравенство:

.

Так как (,)_t>0 - супермартингал, то М() ≤ 0. Отсюда следует неравенство

. Доказательство закончено.

3.2.2. Доказательство теоремы 6.  Предположим, что у последовательности  не существует конечного предела. Через В обозначим множество 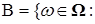 не имеет конечного предела}. Наше предположение выполнено, если:

1)   Р - п. н.,

2)  Р - п. н.

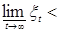
Обозначим: А}, C=}. Очевидно, что , поэтому . Значит для доказательства теоремы достаточно доказать, что Р(А) =0 и Р(С)=0.

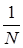
         Покажем, что Р(А)=0. В силу неравенства Чебышева и леммы Фату имеем Р(. Устремляя теперь , получаем Р(А)=0.

Теперь докажем, что Р(С)=0. Заметим, что

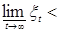
, где  и  - рациональные числа}==.

Рассмотрим вероятность Р(N) в силу неравенства Чебышева и леммы 8 мы имеем:

Р(N).

Капитуляция Афин - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Устремляя теперь , получаем неравенство Р(N). Отсюда следует, что Р(, т.е.Р(С)=0. Доказательство закончено.

3.3. Определение. Мартингал  называется равномерно интегрируемым, если .

Теорема 9. Пусть  равномерно интегрируемый мартингал, тогда Р -п.н. существует случайная величина   такая, что:

а) =  Р - п. н.,

б) М|- Р - п. н.

Доказательство этой теоремы следует из теоремы 6.