Обобщённые линейные гипотезы
9.3. Обобщённые линейные гипотезы
В данном разделе рассматривается проверка обобщённых гипотез H0: Сb=0 и H0: Сb=t. Гипотеза H0: Сb=t является более обобщённой, так как гипотеза H0: Сb=0 получается из неё, если принять вектор t=0. Начнём с гипотезы H0: Сb=0.
Проверка гипотезы H0: Сb=0
Гипотеза H0: Сb=0 с матрицей С размеров qxр и ранга q≤р, элементами которой являются некоторые числа, известна как обобщённая линейная гипотеза, имеющая альтернативную гипотезу H1: Сb≠0. Частными случаями гипотезы H0: Сb=0 являются гипотезы разделов 9.1 и 9.2. Так, гипотеза H0: b1=0 из раздела 9.1 может быть представлена в виде гипотезы H0: Сb=0 следующим образом:
H0: Сb=[0, Iр–1] =b1=0 [в силу (П.3.2)],
=b1=0 [в силу (П.3.2)],
где 0 – вектор нулей размеров (р–1)х1. Аналогичным образом, гипотеза H0: b2=0 из раздела 9.2 тоже может быть представлена в виде гипотезы H0: Сb=0:
H0: Сb=[О, Ih] =b2=0,
=b2=0,
где матрица О нулей размеров hх(р–h) и вектор 0 размеров hх1.
Гипотеза H0: Сb=0 позволяет формулировать и проверять также и более сложные гипотезы. Например, гипотезу
Рекомендуемые материалы
H0: 2b1–b2=b2–2b3+3b4=b1–b4=0
можно представить следующим образом:
H0: 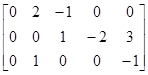
 =
= .
.
В качестве другого примера гипотезу H0: b1=b2=b3=b4 можно представить разностями параметров в виде H0: b1–b2=b2–b3=b3–b4=0 и, следовательно, также в виде обобщённой гипотезы H0: Сb=0:
H0: 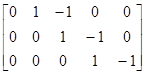
 =
= .
.
В следующей теореме рассматриваются суммы квадратов используемые при проверке гипотезы H0: Сb=0 в сравнении с гипотезой H1: Сb≠0, а также свойства этих сумм квадратов. В ней показано, что вектор Сb имеет ковариационную матрицу s2C(XТX)–1CТ. Следовательно, представляет интерес связанная с обобщённой гипотезой сумма квадратов SH в виде квадратичной формы относительно вектора Сb с матрицей [C(XТX)–1CТ]–1. При этом заметим, что обратная матрицы СT(XTX)–1CТ существует, так как С имеет полный ранг по строкам и матрица XTX симметричная.
Теорема 9.3.1. Если вектор у имеет нормальное распределение Nn(Xb, s2I) и матрица С размеров qxр и имеет ранг q≤р, то:
- Вектор C
![]() имеет нормальное распределение Nq[Сb, s2C(XТX)–1CТ],
имеет нормальное распределение Nq[Сb, s2C(XТX)–1CТ], - Величина SH/s2=(C
![]() )Т[C(XТX)–1CТ]–1C
)Т[C(XТX)–1CТ]–1C![]() /s2 имеет нецентральное распределение c2(q, g) с параметром нецентральности g=(Сb)Т[C(XТX)–1CТ]–1Сb/(2s2),
/s2 имеет нецентральное распределение c2(q, g) с параметром нецентральности g=(Сb)Т[C(XТX)–1CТ]–1Сb/(2s2), - Величина SE/s2=yТ[I–X(XТX)–1XТ]у/s2 имеет центральное распределение c2(п–р),
- Суммы SH и SE статистически независимы.
Доказательство:
- По пункту 1 теоремы 7.3.4 вектор
![]() имеет нормальное распределение Nр[b, s2(XТX)–1]. Следовательно, по пункту 2 теоремы 4.5.2 вектор C
имеет нормальное распределение Nр[b, s2(XТX)–1]. Следовательно, по пункту 2 теоремы 4.5.2 вектор C![]() также имеет нормальное распределение Nq[Сb, s2C(XТX)–1CТ].
также имеет нормальное распределение Nq[Сb, s2C(XТX)–1CТ]. - Вектор C
![]() имеет нормальное распределение и ковариационную матрицу С(C
имеет нормальное распределение и ковариационную матрицу С(C![]() ) =s2C(XТX)–1CТ. Делённая на дисперсию s2 сумма квадратов SH для обобщённой гипотезы H0: Сb=0 записывается в виде квадратичной формы
) =s2C(XТX)–1CТ. Делённая на дисперсию s2 сумма квадратов SH для обобщённой гипотезы H0: Сb=0 записывается в виде квадратичной формы
SH/s2=(C )Т[C(XТX)–1CТ]–1C
)Т[C(XТX)–1CТ]–1C /s2.
/s2.
Произведение матрицы этой квадратичной формы и ковариационной матрицы вектора C даёт идемпотентную матрицу s2[C(XТX)–1CТ]–1C(XТX)–1CТ/s2=I. Следовательно, по теореме 5.5 квадратичная форма SH/s2 имеет нецентральное распределение c2(q, g) с параметром нецентральности
даёт идемпотентную матрицу s2[C(XТX)–1CТ]–1C(XТX)–1CТ/s2=I. Следовательно, по теореме 5.5 квадратичная форма SH/s2 имеет нецентральное распределение c2(q, g) с параметром нецентральности
g=(Сb)Т[C(XТX)–1CТ]–1Сb/(2s2).
- Этот пункт доказан в пункте 2 теоремы 9.1.2.
- Так как при доказательстве пункта 3 теоремы 7.3.4 установлено, что вектор
![]() и сумма SE статистически независимы, то и суммы SH= (C
и сумма SE статистически независимы, то и суммы SH= (C![]() )Т[C(XТX)–1CТ]–1C
)Т[C(XТX)–1CТ]–1C![]() и SE также статистически независимы [Себер (1980) стр. 26, 40-41]. Для более формального доказательства подставим
и SE также статистически независимы [Себер (1980) стр. 26, 40-41]. Для более формального доказательства подставим ![]() =(XТX)–1XТу в выражение суммы SH и представим результат в виде квадратичной формы относительно вектора у
=(XТX)–1XТу в выражение суммы SH и представим результат в виде квадратичной формы относительно вектора у
SH=уТX(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1XТу.
Сумма SE является квадратичной формой относительно вектора у вида
SE=yT[I–X(XТX)–1XТ]y.
Произведения матриц этих квадратичных форм дают нулевую матрицу. Отсюда по следствию 1 теоремы 5.6.2 квадратичные формы SH и SE статистически независимы.
□
Проверка гипотезы H0: Сb=0 в сравнении с гипотезой H1: Сb≠0 на основе статистики FH даётся в следующей теореме.
Теорема 9.3.2. Пусть вектор у имеет нормальное распределение Nn(Xb, s2I) и для проверки гипотезы H0: Сb=0 статистика FHс определяется выражением
FHс=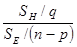
= , (9.3.1)
, (9.3.1)
где матрица С размеров qxр и имеет ранг q≤р, а  =(XТX)–1XТy. Тогда статистика FH имеет следующие распределения:
=(XТX)–1XТy. Тогда статистика FH имеет следующие распределения:
- Если гипотеза H0: Сb=0 ложна, то FHс имеет нецентральное распределение F(q, п–p, g) с параметром не центральности g= (Сb)Т[C(XТX)–1CТ]–1Сb/(2s2).
- Если H0: Сb=0 верна, то FHс имеет центральное распределение F(q, п–р).
Доказательство:
- Этот пункт доказывается в силу (5.4.3) и с использованием теоремы 9.3.1.
- Этот пункт доказывается в силу (5.4.1) и с использованием теоремы 9.3.1.
□
В теореме 9.3.2 проверку гипотезы H0: Сb=0 по статистике FHс называют обычно проверкой обобщенной линейной гипотезы. Число q степеней свободы - это число линейных комбинаций произведения Сb. Проверка гипотезы H0: Сb=0 делается следующим образом. Гипотеза H0: Сb=0 ложна, если рассчитываемое по формуле (9.3.1) значение статистики FHс получается больше критического значения Fкр имеющей центральное распределение F(q, п–р) случайной переменной и выбранную интегральную вероятности 1–α на интервале от 0 до Fкр. Гипотеза H0: Сb=0 также ложна, если статистика FHс имеет пи-значение меньшее α.
Так как по следствию 1 теоремы П.6.2 матрица C(XТX)–1CТ положительно определённая и, если гипотеза H0 ложна, то g>0, где g= (Сb)Т[C(XТX)–1CТ]–1Сb/(2s2). Таким образом, при увеличении значения статистики FHс гипотеза H0: Сb=0 стремится быть ложной.
Пример 9.3.1. Рассмотрим переменную отклика с данными коэффициента усиления транзистора из таблицы 8.3. Для модели у=b0+b1x1+b2x2+ε с не ортогональными и ортогональными векторами значений нормированных факторов проверим гипотезу H0: b1=–3b2, используя вычисляемую по формуле (9.3.1) статистику FHс. Чтобы представить гипотезу H0: b1=–3b2 в виде Сb=0, запишем её так H0: b1+3b2=0. Тогда матрица С=[0, 1, 3] и для модели с не ортогональными векторами значений нормированных факторов произведение C =9,550, а с ортогональными векторами значений нормированных факторов произведение C
=9,550, а с ортогональными векторами значений нормированных факторов произведение C =4,818. Расчёт статистики FHс для этих двух случаев делается соответственно по формулам
=4,818. Расчёт статистики FHс для этих двух случаев делается соответственно по формулам
FHс= и FHсо=
и FHсо= ,
,
где q=1, SE/(n–p)=yT(I–X(XТX)–1XТ)y/(n–p)=yT(I–Xo(XoТXo)–1XoТ)y/(n–p), n=14 и р=3. В результате имеем FHс=2,971х10–3 и FHсо=7,973х10–4. Оба полученных значения значительно меньше критического значения Fкр=4,844 при выбранной интегральной вероятности 0,95. Следовательно, гипотеза H0: b1=–3b2 верна в обоих случаях.
□
В теоремах 9.3.1 и 9.3.2 сумму SH можно записать в виде
SH=(С –0)Т[C(XТX)–1CТ]–1(С
–0)Т[C(XТX)–1CТ]–1(С –0),
–0),
что является возведённым в квадрат расстоянием между С и гипотетическим значением Сb=0, нормированным ковариационной матрицей вектора С
и гипотетическим значением Сb=0, нормированным ковариационной матрицей вектора С . Интуитивно, если гипотеза H0: Сb=0 верна, то вектор С
. Интуитивно, если гипотеза H0: Сb=0 верна, то вектор С имеет тенденцию быть равным приблизительно 0, так что числитель выражения (9.3.1) мал. С другой стороны, если Сb сильно отличается от 0, то числитель выражения (9.3.1) имеет тенденцию увеличиваться.
имеет тенденцию быть равным приблизительно 0, так что числитель выражения (9.3.1) мал. С другой стороны, если Сb сильно отличается от 0, то числитель выражения (9.3.1) имеет тенденцию увеличиваться.
Ожидаемые значения числителя и знаменателя статистики FHс даются в виде
E(SH/q)=s2+(Сb)Т[C(XТX)–1CТ]–1(Сb)/q и E[SE/(п–р)]=s2. (9.3.2)
Эти ожидаемые значения средних квадратичных дают дополнительную мотивацию отклонить гипотезу H0: Сb=0 при больших значениях статистики FHс. Если гипотеза H0: Сb=0 верна, то оба ожидаемых значения средних квадратичных равны s2. Если гипотеза H0: Сb=0 ложна, то E(SH/q)>E[SE/(п–р)].
Статистика FHс по формуле (9.3.1) инвариантна к линейным полного ранга преобразованиям влияющих на отклик факторов и переменных отклика. Это доказывается в следующей теореме.
Теорема 9.3.3. Пусть даны преобразования v=су и W=XK, где K невырожденная матрица, вид которой показан в доказательстве следствия 1 теоремы 7.5. После этих преобразований вычисляемая по формуле (9.3.1) статистика FHс не меняется.
Доказательство: Линейное преобразование данных в матрице Х значений факторов может быть выполнено в виде W=XK. Вектор оценки параметров модели с преобразованной матрицей W получается по формуле
 =(WТW)–1WТу=(KТXТXK)–1KТXТу
=(WТW)–1WТу=(KТXТXK)–1KТXТу
=K–1(XТX)–1XТу=K–1 .
.
Регрессионная сумма квадратов с преобразованной матрицей модели имеет вид
 ТWТу=уТW(WТW)–1WТу=уТXK(KТXТXK)–1KТXТу
ТWТу=уТW(WТW)–1WТу=уТXK(KТXТXK)–1KТXТу
=уТXKK–1(XТX)–1(KТ)–1KТXТу=уТX(XТX)–1XТу
= XТу.
XТу.
Поэтому сумма квадратов остатков SE=yTy– XТу инвариантна к полного ранга линейному преобразованию W=XK матрицы модели. Заметим, что в числителе формулы (9.3.1) матрица С преобразуется таким же образом, как и матрица Х, так что Сw
XТу инвариантна к полного ранга линейному преобразованию W=XK матрицы модели. Заметим, что в числителе формулы (9.3.1) матрица С преобразуется таким же образом, как и матрица Х, так что Сw =СKK–1
=СKK–1 =С
=С . Следовательно числитель формулы (9.3.1) становится
. Следовательно числитель формулы (9.3.1) становится
(Сw )Т[Сw(WТW)–1СwТ]–1Сw
)Т[Сw(WТW)–1СwТ]–1Сw =(С
=(С )Т[СK(KТXТXK)–1(СK)Т]–1С
)Т[СK(KТXТXK)–1(СK)Т]–1С
=(С )Т[С(XТX)–1СТ]–1С
)Т[С(XТX)–1СТ]–1С .
.
Линейное преобразование переменных отклика вида v=су также не меняет рассчитываемую по формуле (9.3.1) статистику FHс. Это получается потому, что суммы SН и SE являются квадратичными формами относительно вектора у. Следовательно, преобразование умножением на постоянное число с добавляет в числителе и знаменателе формулы (9.3.1) по два множителя с, которые сокращаются и эта формула остаётся неизменной.
□
Проверка одного параметра и линейной комбинации параметров
Проверка гипотезы об одном параметре bj модели может быть выполнена рассмотрением адекватной и неадекватной моделей, как показано в разделе 9.2, или методом обобщённой линейной гипотезы. Статистика для проверки гипотезы H0: bр–1=0 с использованием адекватной и неадекватной моделей находится по формуле (9.2.14)
FH= (9.3.3)
(9.3.3)
и, если гипотеза H0: bр–1=0 верна, то FH имеет распределение F(1, п–р). В этом случае параметр bр–1 является последним элементом разделённого вектора b= , при соответствующем разделении матрицы X= [Х1, хр–1], где хр–1 - последний её столбец. Тогда матрица Х1 неадекватной модели у=Х1b1*+e содержит все столбцы матрицы X кроме последнего.
, при соответствующем разделении матрицы X= [Х1, хр–1], где хр–1 - последний её столбец. Тогда матрица Х1 неадекватной модели у=Х1b1*+e содержит все столбцы матрицы X кроме последнего.
Чтобы проверить гипотезу H0: bj=0 с использованием обобщённой линейной гипотезы H0: Сb=0, рассмотрим сначала проверку гипотезы H0: aTb=0 для линейной комбинации параметров, например, aTb= [0, 2, –2, 3, 1]b. Используя aT вместо матрицы С в Сb=0, имеем q=1 и выражение (9.3.1) преобразуется к виду
FHа=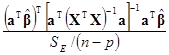
= , (9.3.4)
, (9.3.4)
где s2=SE/(п–р). Если гипотеза H0: aTb=0 верна, то статистика FHа по формуле (9.3.4) имеет распределение F(1, п–р).
Для проверки гипотезы H0: bj=0 об одном параметре с использованием статистики по формуле (9.3.4), пусть aT= [0, ..., 0, 1, 0, ..., 0], где 1 находится в j-ой позиции. Это даёт преобразованную формулу расчёта статистики
FHj= , (9.3.5)
, (9.3.5)
где gjj - j-й диагональный элемент матрицы (XТX)–1. Если гипотеза H0: bj=0 верна, то статистика FHj имеет распределение F(1, п–р). Гипотеза H0: bj=0 ложна, если статистика FHj больше критического значения Fкр имеющей центральное распределение F(q, п–р) случайной переменной с вероятностью 1–α на интервале от 0 до Fкр или, что то же самое, если статистика FHj имеет пи-значение меньше α.
Так как статистика FHj по формуле (9.3.5) имеет распределение F(1, п–р), то чтобы проверить параметр bj в отдельности от других параметров, в силу (5.4.9), можно использовать статистику с распределением t вычисляемую по формуле
tj= . (9.3.6)
. (9.3.6)
Как указано в конце раздела 6.3, гипотеза H0: bj=0 ложна, если |tj|>tα/2(п–р) или, что то же самое, если пи-значение статистик tj меньше α. Для проверки по двустороннему критерию как этот, пи-значение равно двойной вероятности того, что критическое значение tα/2(п–р) распределения t(п–р) превышает абсолютное значение вычисляемой статистики tj.
Для j=1 выражение (9.3.6) становится t1= , что не то же, как в (6.3.12), где t1=
, что не то же, как в (6.3.12), где t1= . Так как пока столбцы матрицы Х неортогональны g11≠
. Так как пока столбцы матрицы Х неортогональны g11≠ .
.
Оценка параметров модели при ограничении Сb=0
Обнаружив, что гипотеза H0: Сb=0 верна, может возникнуть необходимость оценить вектор b параметров модели при ограничении Сb=0. Искомый вектор  оценки находится методом наименьших квадратов путём поиска минимума функции (y–Xb)T(y–Xb) с учётом указанного ограничения.
оценки находится методом наименьших квадратов путём поиска минимума функции (y–Xb)T(y–Xb) с учётом указанного ограничения.
Теорема 9.3.4. Для модели у=Xb+e с ограничением Cb=0 оценкой вектора b её параметров является вектор  =
= –(XТX)–1CТ[C(XТX)–1CТ]–1C
–(XТX)–1CТ[C(XТX)–1CТ]–1C , где
, где  = (XТX)–1XТy.
= (XТX)–1XТy.
Доказательство: Используя вектор l множителей Лагранжа, найдём минимум функции u(b, l)= (у–Xb)Т(у–Xb)+lТCb относительно векторов b и l. Для этого возьмём производную функции u(b, l) по l и приравняем её нулевому вектору, чтобы получить
 =Cb=0.
=Cb=0.
Так как функцию u(b, l) можно преобразовать к виду
u(b, l)=уТу–уТXb–bТXТу+bТXТXb+lТCb
=уТу–2bТXТу+bТXТXb+lТCb,
то её производная по вектору b получается  =0–2XТу+2XТXb+CТl. Приравнивая её нулевому вектору, получаем
=0–2XТу+2XТXb+CТl. Приравнивая её нулевому вектору, получаем
b= –(XТX)–1CТl/2. (9.3.7)
–(XТX)–1CТl/2. (9.3.7)
Умножение это выражение слева на С даёт Сb=С –С(XТX)–1CТl/2. А так как Cb=0, то и С
–С(XТX)–1CТl/2. А так как Cb=0, то и С –С(XТX)–1CТl/2=0. Решение последнего уравнения относительно l, даёт l=2[С(XТX)–1CТ]–1С
–С(XТX)–1CТl/2=0. Решение последнего уравнения относительно l, даёт l=2[С(XТX)–1CТ]–1С . Подстановкой полученного выражения в (9.3.7) вместо l получаем
. Подстановкой полученного выражения в (9.3.7) вместо l получаем
 =
= –(XТX)–1CТ[C(XТX)–1CТ]–1C
–(XТX)–1CТ[C(XТX)–1CТ]–1C . (9.3.8)
. (9.3.8)
Вектор  оценки параметров модели получен при ограничении Cb=0, а вектор
оценки параметров модели получен при ограничении Cb=0, а вектор  является оценкой параметров модели без этого ограничения.
является оценкой параметров модели без этого ограничения.
Для подтверждения, что найденный вектор  оценки даёт минимальное значение функции u(b, l), возьмём вторую производную от этой функции по b. Она получается
оценки даёт минимальное значение функции u(b, l), возьмём вторую производную от этой функции по b. Она получается  =XТX. Матрица XТX положительно определённая, следовательно при найденном векторе
=XТX. Матрица XТX положительно определённая, следовательно при найденном векторе  функция u(b, l) принимает минимальное значение.
функция u(b, l) принимает минимальное значение.
□
Имея оценку вектора b при ограничении Cb=0, найдём теперь сумму квадратов остаточных ошибок модели с этим ограничением. Эта сумма квадратов
(y–X )T(y–X
)T(y–X ) =[y–X
) =[y–X +X(
+X( –
– )]T[y–X
)]T[y–X +X(
+X( –
– )]
)]
= (y–X )T(y–X
)T(y–X )+(
)+( –
– )TXTX(
)TXTX( –
– ) (9.3.9)
) (9.3.9)
с другими членами равными нулю, так как XT(y–X )=0. Далее, в силу (9.3.8), имеем
)=0. Далее, в силу (9.3.8), имеем
 –
– =(XТX)–1CТ[C(XТX)–1CТ]–1C
=(XТX)–1CТ[C(XТX)–1CТ]–1C
и, подставляя это в (9.3.9), получаем
(y–X )T(y–X
)T(y–X )=SE+(C
)=SE+(C )T[C(XТX)–1CТ]–1С(XTX)–1XTX(XТX)–1CТ[C(XТX)–1CТ]–1C
)T[C(XТX)–1CТ]–1С(XTX)–1XTX(XТX)–1CТ[C(XТX)–1CТ]–1C
=SE+(C )T[C(XТX)–1CТ]–1C
)T[C(XТX)–1CТ]–1C
=SE+SНс, (9.3.10)
где SE =(y–X )T(y–X
)T(y–X ) и SНс=(C
) и SНс=(C )T[C(XТX)–1CТ]–1C
)T[C(XТX)–1CТ]–1C .
.
Если Сb≠0, то оценка  по формуле (9.3.8) является смещённой оценкой вектора b, но дисперсии элементов вектора
по формуле (9.3.8) является смещённой оценкой вектора b, но дисперсии элементов вектора  меньше дисперсий элементов вектора
меньше дисперсий элементов вектора  , что показано в следующей теореме.
, что показано в следующей теореме.
Теорема 9.3.5. Математическое ожидание вектора  оценки по формуле (9.3.8) и его ковариационная матрица соответственно следующие:
оценки по формуле (9.3.8) и его ковариационная матрица соответственно следующие:
- E(
![]() ) =b–(XТX)–1CТ[C(XТX)–1CТ]–1Cb. (9.3.11)
) =b–(XТX)–1CТ[C(XТX)–1CТ]–1Cb. (9.3.11) - С(
![]() ) =s2{(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1}. (9.3.12)
) =s2{(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1}. (9.3.12)
Доказательство:
- E(
![]() ) =E(
) =E(![]() )–(XТX)–1CТ[C(XТX)–1CТ]–1CE(
)–(XТX)–1CТ[C(XТX)–1CТ]–1CE(![]() )
)
=b–(XТX)–1CТ[C(XТX)–1CТ]–1Cb. [в силу (7.2.9)]
- С(
![]() )=С({I–(XТX)–1CТ[C(XТX)–1CТ]–1C}
)=С({I–(XТX)–1CТ[C(XТX)–1CТ]–1C}![]() )
)
=С(B )=BС(
)=BС( )BТ=s2B(XТX)–1BТ. [в силу (3.6.10) и (7.2.10)]
)BТ=s2B(XТX)–1BТ. [в силу (3.6.10) и (7.2.10)]
А так как
B(XТX)–1BТ={I–(XТX)–1CТ[C(XТX)–1CТ]–1C}(XТX)–1{I–(XТX)–1CТ[C(XТX)–1CТ]–1C}Т
={(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1}{I–CТ[C(XТX)–1CТ]–1C(XТX)–1}
=(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1
+(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1
=(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1,
то
С( ) =s2{(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1}.
) =s2{(XТX)–1–(XТX)–1CТ[C(XТX)–1CТ]–1C(XТX)–1}.
□
Так как вторая матрица в правой части выражения (9.3.12) является неотрицательно определённой, то диагональные элементы ковариационной матрицы С( ) меньше диагональных элементов ковариационной матрицы С(
) меньше диагональных элементов ковариационной матрицы С( )=s2(XТX)–1, то есть, D(
)=s2(XТX)–1, то есть, D( )≤D(
)≤D( ) при j=0, 1, 2, …, р–1, где D(
) при j=0, 1, 2, …, р–1, где D( ) - j-й диагональный элемент матрицы С(
) - j-й диагональный элемент матрицы С( ) в (9.3.12). Это аналогично неравенству D(
) в (9.3.12). Это аналогично неравенству D( )>D(
)>D( ) пункта 1 теоремы 8.2.3, где
) пункта 1 теоремы 8.2.3, где  - результаты оценки параметров неадекватной модели.
- результаты оценки параметров неадекватной модели.
Проверка гипотезы H0: Сb=t
Все рассмотренные выше и другие линейные гипотезы являются частными случаями и могут быть представлены одной обобщённой гипотезой H0: Сb=t, где b - вектор размеров рх1 параметров модели, С - любая матрица чисел размеров qхр и t - вектор размеров qх1 определённых чисел. Гипотеза H0: Сb=t является обобщением гипотезы H0: Сb=0. С использованием вектора t можно проверить, например, гипотезу H0: b2=b1+5.
Матрица С должна иметь полный ранг по строкам ранг(С)=q. Это значит, что образующие гипотезу линейные функции вектора b должны быть линейно независимы. Гипотеза должна состоять из линейно независимых функций вектора b, то есть не должна содержать функции, являющиеся линейными комбинациями остальных её функций. Например, если гипотеза включает функции b1–b2 и b2–b3, то нет смысла включать функцию b1–b3, являющуюся суммой функции b1–b2 и b2–b3. В реальных исследованиях это требование к матрице С не ограничивает использование гипотезы H0: Сb=t.
Может также возникнуть требование к вектору t чтобы уравнения Сb=t были совместными, то есть, чтобы ранг(C)=ранг[C, t] (см. теорему П.7). Однако это достигается автоматически, если матрица С имеет полный ранг по строкам, и поэтому уравнения Сb=t совместны для любого вектора t.
Для проверки гипотезы H0: Сb=t необходима имеющая распределение F статистика. Требуемые для её получения суммы квадратов и их свойства приведены в следующей теореме.
Теорема 9.3.6. Если вектор у имеет нормальное распределение Nn(Xb, s2I), а матрица С размеров qxр и имеет ранг q≤р, то:
- Вектор C
![]() –t имеет нормальное распределение Nq[Сb–t, s2C(XТX)–1CТ],
–t имеет нормальное распределение Nq[Сb–t, s2C(XТX)–1CТ], - Величина SHt/s2= (C
![]() –t)Т[C(XТX)–1CТ]–1(C
–t)Т[C(XТX)–1CТ]–1(C![]() –t)/s2 имеет нецентральное распределение c2(q, g) с параметром g= (Cb–t)Т[C(XТX)–1CТ]–1(Cb–t)/2s2,
–t)/s2 имеет нецентральное распределение c2(q, g) с параметром g= (Cb–t)Т[C(XТX)–1CТ]–1(Cb–t)/2s2, - Величина SE/s2=yТ[I–X(XТX)–1XТ]у/s2 имеет центральное распределение c2(п–р).
- Суммы SHt и SE статистически независимы.
Доказательство:
- По пункту 1 теоремы 7.3.4 вектор
![]() имеет нормальное распределение Nр[b, s2(XТX)–1]. Следовательно, по следствию 1 теоремы 4.5.2 вектор C
имеет нормальное распределение Nр[b, s2(XТX)–1]. Следовательно, по следствию 1 теоремы 4.5.2 вектор C![]() –t тоже имеет нормальное распределение Nq[Сb–t, s2C(XТX)–1CТ].
–t тоже имеет нормальное распределение Nq[Сb–t, s2C(XТX)–1CТ]. - Вектор C
![]() –t имеет ковариационную матрицу С(C
–t имеет ковариационную матрицу С(C![]() –t) =s2C(XТX)–1CТ. Следовательно, по аналогии с доказательством пункта 2 теоремы 9.3.1, величина SHt/s2= (C
–t) =s2C(XТX)–1CТ. Следовательно, по аналогии с доказательством пункта 2 теоремы 9.3.1, величина SHt/s2= (C![]() –t)Т[C(XТX)–1CТ]–1(C
–t)Т[C(XТX)–1CТ]–1(C![]() –t)/s2 имеет нецентральное распределение c2(q, g) с параметром g= (Cb–t)Т[C(XТX)–1CТ]–1(Cb–t)/(2s2) и
–t)/s2 имеет нецентральное распределение c2(q, g) с параметром g= (Cb–t)Т[C(XТX)–1CТ]–1(Cb–t)/(2s2) и
SHt/s2~c2{q, (С –t)T[С(XTX)–1СT]–1(С
–t)T[С(XTX)–1СT]–1(С –t)/(2s2)}. (9.3.13)
–t)/(2s2)}. (9.3.13)
- Доказательство этого пункта дано в пункте 2 теоремы 9.1.2.
- Так как по пункту 3 теоремы 7.3.4 вектор
![]() и SE независимы, то SHt и SE тоже независимы [Себер (1980) стр. 26, 40-41]. Для более формального доказательства представим SHt и SE в виде квадратичных форм относительно одного и того же нормально распределенного вектора. Подставляя (XTX)–1XTy вместо
и SE независимы, то SHt и SE тоже независимы [Себер (1980) стр. 26, 40-41]. Для более формального доказательства представим SHt и SE в виде квадратичных форм относительно одного и того же нормально распределенного вектора. Подставляя (XTX)–1XTy вместо ![]() , выражение для SHt принимает вид
, выражение для SHt принимает вид
SHt= [С(XTX)–1XTy–t]T[С(XTX)–1СT]–1[С(XTX)–1XTy–t].
Но, так как С имеет полный ранг по строкам, то по следствию 1 теоремы П.6.4 существует (ССT)–1. Следовательно, можно записать
С(XTX)–1XTy–t=С(XTX)–1XT[y–XСT(ССT)–1t]
и, с учётом этого,
SHt=[y–XСT(ССT)–1t]TX(XTX)–1СT[С(XTX)–1СT]–1С(XTX)–1XT[y–XСT(ССT)–1t].
Теперь рассмотрим сумму квадратов остатков SE=yT[I–X(XTX)–1XT]y. Так как имеем XT[I–X(XTX)–1XT]=О и [I–X(XTX)–1XT]X=О, то выражение для SE можно переписать в виде
SE=[y–XСT(ССT)–1t]T[I–X(XTX)–1XT][y–XСT(ССT)–1t].
Обе суммы SHt и SE представлены в виде квадратичных форм относительно вектора y–XСT(ССT)–1t. Этот вектор имеет распределение Nп[Хb–XСT(ССT)–1t, s2I], так как Е(y–XСT(ССT)–1t)=Хb–XСT(ССT)–1t и D(y–XСT(ССT)–1t)= s2I. И, хотя уже известно, что SHt/s2 и SE/s2 имеют распределения c2, это видно также из того, что они квадратичные формы относительно вектора y–XСT(ССT)–1t с распределением по нормальному закону и матрицы этих квадратичных форм идемпотентные. Произведение этих двух матриц равно нулевой матрице
[I–X(XTX)–1XT]X(XTX)–1СT[С(XTX)–1СT]–1С(XTX)–1XT=О.
Поэтому по теореме 5.6.2 квадратичные формы SHt и SE распределены независимо.
□
Проверка гипотезы H0: Сb=t в сравнении с гипотезой H1: Сb≠t дается в следующей теореме.
Теорема 9.3.7. Пусть вектор у имеет нормальное распределение Nn(Xb, s2I) и статистика FHt определена следующим образом
FHt=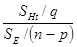
= , (9.3.14)
, (9.3.14)
где  =(XТX)–1XТy. Распределения данной этим выражением статистики FHt получаются следующими:
=(XТX)–1XТy. Распределения данной этим выражением статистики FHt получаются следующими:
- Если гипотеза H0: Сb=t ложна, то статистика FHt принимает нецентральное распределение F(q, п–р, g) c параметром g= (Сb–t)Т[C(XТX)–1CТ]–1(Сb–t)/(2s2).
- Если гипотеза H0: Сb=t верна, то g=0 и статистика FHt обретает центральное распределение F(q, п–р).
Доказательство:
- Доказывается с использованием теоремы 9.3.6 и выражения (5.4.3).
- Доказывается с использованием теоремы 9.3.6 и выражения (5.4.1).
□
Следовательно, статистика FHt обеспечивает проверку гипотезы H0: Сb=t. Проверка гипотезы H0: Сb=t осуществляется следующим образом. Гипотеза H0: Сb=t ложна, если расчётное значение статистики FHt больше критического значения Fкр имеющей центральное распределение F(q, п–р) случайной переменной при выбираемой на интервале от 0 до Fкр интегральной вероятности равной 1–α. Или по-другому, гипотеза H0: Сb=t ложна, если пи-значение статистики FHt меньше α.
Ожидаемые значения средних квадратичных для проверки по статистике FHt даются в виде
E(SHt/q)=s2+(Сb–t)Т[C(XТX)–1CТ]–1(Сb–t)/q и E[SE/(п–р)]=s2. (9.3.15)
Универсальность этой проверки заслуживает особого внимания. Она применима для любой линейной гипотезы Сb=t при одном условии, что матрица С имеет полный ранг по строкам. При этом статистика FHt может использоваться для проверки любой линейной гипотезы. Проверяемая линейная гипотеза должна быть только записана в виде Сb=t и статистика FHt позволяет её проверить. Имея решение нормальных уравнения для модели у=Xb+e и найденными (XTX)–1,  =(XTX)–1XTy и SE/(п–р), проверка гипотезы H0: Сb=t выполняется прямым использованием статистики FHt. Обратим внимание, что величина SE/(п–р) остаётся постоянной для любого применения статистики FHt. Таким образом, при рассмотрении различных гипотез единственное, что изменяется в статистике FHt, это SHt/q.
=(XTX)–1XTy и SE/(п–р), проверка гипотезы H0: Сb=t выполняется прямым использованием статистики FHt. Обратим внимание, что величина SE/(п–р) остаётся постоянной для любого применения статистики FHt. Таким образом, при рассмотрении различных гипотез единственное, что изменяется в статистике FHt, это SHt/q.
Оценка параметров при ограничении Сb=t
При обнаружении, что гипотеза H0: Сb=t верна, может возникнуть потребность оценить вектор b параметров модели при ограничении Сb=t. Вектор b оценки в этом случае, также как и при ограничении Сb=0, находится методом наименьших квадратов с учётом указанного ограничения и использованием метода множителей Лагранжа.
Теорема 9.3.6. Для модели у=Xb+e с ограничением Cb=t оценка вектора b её параметров делается по формуле b= –(XТX)–1CТ[C(XТX)–1CТ]–1(С
–(XТX)–1CТ[C(XТX)–1CТ]–1(С –t), где вектор
–t), где вектор  =(XТX)–1XТy.
=(XТX)–1XТy.
Доказательство: Используя вектор l множителей Лагранжа найдём минимум функции u(b, l)= (у–Xb)Т(у–Xb)+lТ(Сb–t) относительно векторов b и l следующим образом. Возьмём производную функции u(b, l) по l и приравняем её нулевому вектору, чтобы получить
 =Сb–t=0
=Сb–t=0
или Сb=t. Так как функция
u(b, l)=уТу–уТXb–bТXТу+bТXТXb+lТ(Сb–t)
=уТу–2bТXТу+bТXТXb+lТ(Сb–t),
то её производная по вектору b имеет вид  =0–2XТу+2XТXb+lТC. Приравнивая эту производную нулевому вектору, получаем
=0–2XТу+2XТXb+lТC. Приравнивая эту производную нулевому вектору, получаем
b= –(XТX)–1CТl/2. (9.3.16)
–(XТX)–1CТl/2. (9.3.16)
Умножая это выражение слева на С имеем Сb=С –С(XТX)–1CТl/2. А так как Cb=t, то С
–С(XТX)–1CТl/2. А так как Cb=t, то С –С(XТX)–1CТl/2=t. Решение последнего уравнения относительно l, даёт l=2[С(XТX)–1CТ]–1(С
–С(XТX)–1CТl/2=t. Решение последнего уравнения относительно l, даёт l=2[С(XТX)–1CТ]–1(С –t). Подставляя полученное выражение обратно в (9.3.16) вместо l, получаем
–t). Подставляя полученное выражение обратно в (9.3.16) вместо l, получаем
b= –(XТX)–1CТ[C(XТX)–1CТ]–1(С
–(XТX)–1CТ[C(XТX)–1CТ]–1(С –t). (9.3.17)
–t). (9.3.17)
Вектор b оценки параметров модели получен при ограничении Cb=t, а вектор  является оценкой параметров модели без этого ограничения.
является оценкой параметров модели без этого ограничения.
Для подтверждения, что найденный вектор b оценки обеспечивает минимальное значение функции u(b, l), возьмём вторую производную от этой функции по b. Она получается  =XТX. Матрица XТX положительно определённая, следовательно при векторе b=b функция u(b, l) принимает минимальное значение.
=XТX. Матрица XТX положительно определённая, следовательно при векторе b=b функция u(b, l) принимает минимальное значение.
□
Имея вектор b оценки параметров модели при ограничении Сb=t, теперь покажем, что соответствующая сумма квадратов остаточных ошибок равна SE+SHt, где SHt - сумма квадратов в числителе статистики FHt, используемой при проверке гипотезы и данной выражением (9.3.14). Сумма квадратов остатков
(y–Xb)T(y–Xb)=[y–X +X(
+X( –b)]T[y–X
–b)]T[y–X +X(
+X( –b)]
–b)]
=(y–X )T(y–X
)T(y–X )+(
)+( –b)TXTX(
–b)TXTX( –b) (9.3.18)
–b) (9.3.18)
с другими членами, исчезающими из-за XT(y–X )=0. Теперь, в силу (9.3.17),
)=0. Теперь, в силу (9.3.17),
 –b=(XTX)–1CТ[С(XTX)–1CТ]–1(С
–b=(XTX)–1CТ[С(XTX)–1CТ]–1(С –t)
–t)
и, подставляя это в (9.3.18), имеем
(y–Xb)T(y–Xb)=SE+(С –t)T[С(XTX)–1CТ]–1С(XTX)–1XTX(XTX)–1CТ[С(XTX)–1CТ]–1(С
–t)T[С(XTX)–1CТ]–1С(XTX)–1XTX(XTX)–1CТ[С(XTX)–1CТ]–1(С –t)
–t)
=SE+(С –t)T[С(XTX)–1CТ]–1(С
–t)T[С(XTX)–1CТ]–1(С –t)
–t)
=SE+SHt. (9.3.19)
Рассмотрим теперь влияние ограничения Сb=t гипотезы H0: Сb=t на модель у=Xb+e.
При оценке вектора b с ограничением Сb=t можно сказать, что на модель у=Xb+e наложено ограничение Сb=t. Назовём исходную модель у=Xb+e моделью без ограничения и эту модель с наложенным ограничением Сb=t назовём моделью с ограничением. Так, если модель без ограничения имеет вид
yi=b0+b1xi1+b2xi2+b3xi3+ei
и гипотезой является Н0: b1=b2, то моделью с ограничением будет
yi=b0+b1(xi1+xi2)+b3xi3+ei.
Теперь проанализируем смысл SHt и SE+SHt в плане сумм квадратов для моделей с ограничением и без него. Пусть получаемые после оценки параметров модели без ограничения регрессионная сумма квадратов будет SR и SE - сумма квадратов остатков. В (9.3.19) установлено, что для модели с ограничением сумма квадратов остатков
SEо=SE+SHt. (9.3.20)
Следовательно, SHt получается в виде
SHt=SEо–SE=SE+SHt–SE, (9.3.21)
что можно записать ещё так
SHt=yTy–SE–[yTy–(SE+SHt)]
=SR–[yTy–(SE+SHt)]. (9.3.22)
Сравнение выражений (9.3.22) и (9.3.21) побуждает сделать вывод, что yTy–(SE+SHt) является регрессионной суммой квадратов модели с ограничением, получаемой после оценки её параметров. Побуждение сделать это усугубляется тем, что SE+SHt является определяемой выражением (9.3.20) суммой квадратов SEо остатков. Тем не менее, для рассматриваемого ограничения Сb=t только в специальных случаях выражение yTy–(SE+SHt) является регрессионной суммой квадратов. Эти специальные случаи достаточно общие и полезные, но они не являются универсальными [Searle (1971) стр. 117].
Сначала покажем, что выражение yTy–(SE+SHt) обычно не является суммой квадратов, так как может быть отрицательным. Например, в выражении
yTy–SE–SHt=SR–SHt= TXTy–(С
TXTy–(С –t)T[С(XTX)–1CТ]–1(С
–t)T[С(XTX)–1CТ]–1(С –t) (9.3.23)
–t) (9.3.23)
второй член справа является неотрицательно определенной квадратичной формой. Поэтому она никогда не бывает отрицательной и, если один или более элементов вектора t достаточно большие, то этот член превысит  TXTy и результат выражения (9.3.23) будет отрицательным. Поэтому выражение yTy–(SE+SHt) не является суммой квадратов.
TXTy и результат выражения (9.3.23) будет отрицательным. Поэтому выражение yTy–(SE+SHt) не является суммой квадратов.
Причиной того, что yTy–SE–SHt не обязательно является регрессионной суммой квадратов для модели с ограничением, является и то, что уТу не всегда общая сумма квадратов для этой модели. Например, если модель без ограничения
yi=b0+b1xi1+b2xi2+ei
и условие гипотезы b1=b2+4, то моделью с ограничением будет
yi=b0+(b2+4)xi1+b2xi2+ei,
т.е., имеем модель
yi–4xi1=b0+b2(xi1+xi2)+ei. (9.3.24)
Общая сумма квадратов для этой модели (y–4x1)T(y–4x1), а не уТу, и поэтому yTy–(SE+SH) не регрессионная сумма квадратов. Кроме этого, модель (9.3.24) не единственная модель с ограничением, так как условие гипотезы b1=b2+4 может также использоваться для преобразования модели к виду
yi=b0+b1xi1+(b1–4)xi2+ei,
то есть получаем другую модель
yi+4xi2=b0+b1(xi1+xi2)+ei. (9.3.25)
Для неё общая сумма квадратов равна (y+4x2)T(y+4x2). Таким образом, в этом случае есть две модели (9.3.24) и (9.3.25) с одним и тем же ограничением и они неодинаковые. Ни одна из их общих сумм квадратов не равна уТу. Поэтому уТу–(SE+SHt) не является регрессионной суммой квадратов модели с ограничением. Действительно, при наличии моделей (9.3.24) и (9.3.25), нет единственной модели с ограничением. Но, несмотря на это, SE+SHt является суммой квадратов остатков для всех возможных моделей с ограничением. Их общие и регрессионные суммы квадратов отличаются от модели к модели, но их суммы квадратов остатков все одинаковы.
Специальный случай модели с ограничением Сb=t
Описанная выше ситуация в целом верна для гипотезы H0: Сb=t [Searle (1971) стр.118]. А если взять произвольную матрицу L такой, что матрица R= имеет полный ранг и её обратная R–1=[P, S], то модель у=Xb+e можно записать в виде
имеет полный ранг и её обратная R–1=[P, S], то модель у=Xb+e можно записать в виде
y=XR–1Rb+e=X[P, S] + e
+ e
=XPt+XSLb+e
или иначе
y–XPt=XSLb+e. (9.3.26)
Специальный случай в котором выражение уТу–(SE+SHt) является регрессионной суммой квадратов для модели с ограничением Сb=t будет при t=0. В этом случае модель (9.3.26) принимает вид
y=XSLb+e
и поэтому общая сумма квадратов для модели с ограничением равна уТу, что то же самое и для модели без ограничения. Следовательно, в этом случае
уТу–(SE+SH) =SRо, (9.3.27)
где SRо - регрессионная сумма квадратов для модели с ограничением. Что это сумма квадратов, то есть является неотрицательно определенной, видно из (9.3.27), где, считая t=0, получаем
yTy–(SE+SH)= TXTy–
TXTy– TСT[С(XTX)–1CТ]–1С
TСT[С(XTX)–1CТ]–1С
=yT{X(XTX)–1XT–X(XTX)–1СT[С(XTX)–1CТ]–1С(XTX)–1XT}y. (9.3.28)
Так как матрица в фигурных скобках идемпотентная, то она неотрицательно определенная. Поэтому так же и значение выражения уТу–(SE+SH) неотрицательно и это сумма квадратов. В силу (9.3.27), имеем
SH=уТу–SE–SRо
и, зная, что уТу–SE=SR - регрессионная сумма квадратов для модели без ограничения, то
SН=SR–SRo
=(C )Т[C(XТX)–1CТ]–1C
)Т[C(XТX)–1CТ]–1C . (9.3.29)
. (9.3.29)
Таким образом, поскольку единственным различием между моделями без ограничения и с ограничением является условие гипотезы, то логично считать SH регрессионной суммой квадратов в результате условия гипотезы.
Вместе с этой лекцией читают "Грибы".
Пример 9.3.2. Во многих случаях моделирования условие гипотезы может быть встроено непосредственно в модель, чтобы получить модель с ограничением. Положим, что исходная модель имеет вид
уi=b0+b1xi1+b2xi2+b3xi3+ei
и гипотезой является H0: b1=2b2. Тогда модель с ограничением в виде условия гипотезы становится
уi=b0+2b2xi1+b2xi2+b3xi3+ei
=b0о+b2о(2xi1+xi2)+b3оxi3+ei,
где biо – параметры модели при ограничении b1=2b2. Оценка параметров может быть сделана для моделей с ограничением и без него и разница S(b2|b1)= ТXТy–
ТXТy– ТXТy будет такой же, как SH в (9.3.29).
ТXТy будет такой же, как SH в (9.3.29).





















