Линейные функции векторов случайных переменных
3.6. Линейные функции векторов случайных переменных
Часто используются линейные комбинации случайных переменных y1, y2,..., уп вектора у. Пусть аТ= [а1, а2,..., ап] - вектор некоторых числовых значений. Тогда, как показано в главе 1, линейная комбинация переменных y1, y2,..., уп с коэффициентами а1, а2,..., ап может быть записана в виде
х=а1y1+a2y2+…+апуп=aTy. (3.6.1)
Рассмотрим средние, дисперсии и ковариации таких линейных комбинаций.
Математические ожидания линейных функций
Так как у - вектор случайных переменных, то линейная комбинация х=aTy является одной случайной переменной. Математическое ожидание или среднее переменной aTy дается в следующей теореме.
Теорема 3.6.1. Если а - вектор размеров пх1 некоторых числовых значений и у - вектор размеров пх1 случайных переменных, имеющий вектор средних y, то среднее переменной х=aTy
x=E(aTy)=aTE(у)=aTy. (3.6.2)
Доказательство: Используя выражения (3.6.1), (3.2.7) и (3.2.6), получаем
Рекомендуемые материалы
E(aTy)=E(а1y1+a2y2+…+апуп)
=E(а1y1)+E(a2y2)+…+(апуп)
=а1E(y1)+a2E(y2)+…+апE(уп)
=[а1, а2,..., ап]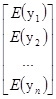
=aTE(y)
=aTy.
□
Положим, что имеются несколько линейных комбинаций переменных вектора у с постоянными коэффициентами:
x1=а11y1+a12y2+…+а1пуп=a1Ty
x2=а21y1+a22y2+…+а2пуп=a2Ty
...
xk=аk1y1+ak2y2+…+аkпуп=akTy,
где aiT=[ai1, ai2,..., аiп] и уT=[y1, y2,..., уп]. Эти k линейных функций можно записать в виде
х=Ay, (3.6.3)
где
х= , A=
, A= =
= .
.
Возможно иметь k >п, но, как правило, k≤п с линейно независимыми строками а1с, а2с, ..., аkc матрицы А, так что она полного ранга. Так как у - вектор случайных переменных, то каждая переменная хi=aiTy является тоже случайной и хT=[х1, х2, ..., хk] является вектором случайных переменных. Ожидаемое среднее значение вектора х=Ay вместе с некоторыми обобщениями дается в следующей теореме.
Теорема 3.6.2. Положим, что у - вектор случайных переменных, X – матрица случайных переменных, а а и b - векторы и А и В - матрицы некоторых числовых значений. Тогда полагая, что матрицы и векторы в каждом произведении имеют соответствующие размеры, получаем следующие математические ожидания:
- E(Ay)=АЕ(у). (3.6.4)
- E(aTXb)=aTE(X)b. (3.6.5)
- E(AXB)=АЕ(Х)B. (3.6.6)
Доказательство: Эти результаты следуют из теоремы 3.6.1.
- Если представить матрицу А в виде её строк, то
Ау= у=
у=
Отсюда по теореме 3.6.1 Е(аicy)=аicЕ(y) и ожидаемое значение E(Ay)=АЕ(у).
- Запишем матрицу Х в виде её столбцов Х=[х1, х2, ..., хп]. Так как Xb - вектор случайных переменных, то по теореме 3.6.1 имеем
E(aTXb)=aTE(Xb)
=aTE(b1х1+b2х2+...+bпхп)
=aT[b1E(х1)+b2E(х2)+...+bпE(хп)]
=aT[E(х1)+E(х2)+...+E(хп)]b
=aTE(X)b.
3. Представляя матрицу А в виде её строк, а матрицу Х в виде её столбцов, получаем E(AXB)=E[ X[b1, b2, ..., bп]
X[b1, b2, ..., bп]
=E =
=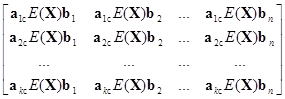
= E[X][b1, b2, ..., bп]=АЕ(Х)B.
E[X][b1, b2, ..., bп]=АЕ(Х)B.
□
Следствие 1. Если А – матрица размеров kхп и b - вектор размеров kх1 некоторых числовых значений, а у - вектор размеров пх1 случайных переменных, то
E(Ay+b)=АЕ(у)+b. (3.6.7)
Доказательство: В силу (3.3.2), имеем E(Ay+b)=E(Ay)+E(b)=AE(y)+b. Покажите, что по определению математического ожидания, если b - вектор некоторых числовых значений, то E(b)=b.
□
Дисперсии и ковариации линейных функций
Дисперсия случайной переменной х=aTy приводится в следующей теореме.
Теорема 3.6.3. Если а - вектор размеров пх1 некоторых числовых значений и у - вектор размеров пх1 случайных переменных, имеющий матрицу S дисперсий и ковариаций, то дисперсия переменной х=aTy дается выражением
D(aTy)=aTSa=sх2. (3.6.8)
Доказательство: В силу (3.2.2) и теоремы 3.6.1, получаем
D(aTy)=E(aTy+aTy)2=E[aT(y+y)]2
=E[aT(y+y)aT(y+y)]
=E[aT(y+y)(y+y)Ta] [так как aT(y+y)=(y+y)Ta]
=aTE[(y+y)(y+y)T]a [по пункту 2 теоремы 3.6.2]
=aTSa . [так как S=E[(y+y)(y+y)T]]
□
Покажем использование выражения (3.6.8) при п=3:
D(aTy) =D(а1y1+a2y2+a3y3)=aTSa=[а1, а2, а3]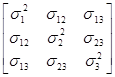
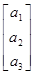
=а12s12+а22s22+а32s32+2а1а2s12+2а1а3s13+2а2а3s23.
Таким образом, дисперсия D(aTy) =aTSa включает все дисперсии и ковариации между переменными y1, y2 и y3.
Ковариация двух линейных комбинаций приведена в следующем следствии теоремы 3.6.3.
Следствие 1. Если а и b - векторы размеров пх1 некоторых числовых значений, то
С(aTу, bTу)=aTSb. (3.6.9)
Доказательство: В силу (3.2.9) и теоремы 3.6.1, получаем
С(aTу, bTу)=Е[(aTy–aTy)(bTy–bTy)T]
=Е[aT(y–y)(y–y)Tb]
=aTЕ[(y–y)(y–y)T]b [по пункту 2 теоремы 3.6.2]
=aTSb.
□
Каждая переменная хi вектора случайных переменных хT= [х1, х2,..., хk] в выражении х=Ay имеет дисперсию и каждая пара переменных хi и хj (i≠j) имеет ковариацию. Эти дисперсии и ковариации находятся в ковариационной матрице вектора х, которая вместе с ковариационной матрицей С(х, w), где w=By - другой набор линейных функций, дается в следующей теореме.
Теорема 3.6.4. Пусть векторы х=Ay и w=By, где матрицы A размеров kхп и В размеров тхп некоторых числовых значений, а у - вектор размеров пх1 случайных переменных, имеющий матрицу S дисперсий и ковариаций. Тогда
- С(х)=С(Ay)=ASAT, (3.6.10)
- С(х, w)=С(Ay, By)=ASBT. (3.6.11)
Доказательство:
1. По пунктам 1 и 2 теоремы 3.6.2 получаем
С(Ay)=Е[(Ay–Ay)(Ay–Ay)T]
=Е[A(y–y)(y–y)TAT]
=AЕ[(y–y)(y–y)T]AT
=ASAT.
2. В силу (3.5.3) и по пункту 1 теоремы 3.6.2, получаем
С(Ay, By)=Е[(Ay–Ay)(Вy–Вy)T]
=Е[A(y–y)(y–y)TВT]
=AЕ[(y–y)(y–y)T]ВT
=ASВT.
□
Как правило, k ≤п и матрица А имеет полный ранг, а в этом случае по следствию 1 теоремы П.6.2 матрица ASAT положительно определённая, если матрица S положительно определённая. Если k >п, то по следствию 2 теоремы П.6.2 матрица ASAT неотрицательно определённая. В этом случае по-прежнему ASAT - матрица ковариаций, но она не может быть использована в числителе или знаменателе многомерной нормальной функции плотности вероятности, данной выражением (4.2.7) в следующей главе.
Обратим внимание, что С(х, w)=ASBT является прямоугольной матрицей размеров kхm, содержащей ковариации каждой переменной хi с каждой переменной wj, то есть, элементами С(х, w) являются С(хi, wj), где i =1, 2,..., k, j =1, 2,..., m. Эти kхm ковариаций можно также найти по отдельности используя выражение (3.6.9).
Следствие 1. Если b - вектор размеров kх1 некоторых числовых значений, то ковариационная матрица вектора Ay+b
С(Ay+b)=ASAT. (3.6.12)
Доказательство: В силу (3.3.4) и (3.6.7), имеем
С(Ay+b)=Е{[Ay+b–(Ay+b)][Ay+b–(Ay+b)]T}
=Е[A(y–y)(y–y)TAT]
=AЕ[(y–y)(y–y)T]AT
=ASAT.
□
Матрица вариаций и ковариаций линейных функций двух различных векторов случайных переменных даётся в следующей теореме.
Теорема 3.6.5. Пусть векторы случайных переменных у размеров пх1 и х размеров qх1 имеют ковариационную матрицу C(у, х) =Syx, а матрицы A размеров kхр и B размеров hхq некоторых числовых значений. Тогда ковариационная матрица векторов Ay и Bx
С(Ay, Bx)=ASyxBT. (3.6.13)
Доказательство: По пункту 2 теоремы 3.6.4 имеем
С(Ay, Bх)=Е[(Ay–Ay)(Вх–Вx)T]
=Е[A(y–y)(x–x)TВT]
=AЕ[(y–y)(x–x)T]ВT
=ASyxВT.
□
Для теоремы 3.6.5 имеются следующие частные случаи:
C(Aу, х)=AC(у, х) и C(у, Bх)=C(у, х)BТ.
Упражнения
3.1. Покажите, что E(ау)=аЕ(у), как в (3.2.6).
3.2. Покажите, что D(ау)=a2s2, как в (3.2.8).
3.3. Покажите, что С(yi, yj)=E(yiyj)–yiyj, как в (3.2.10).
3.4. Покажите, что если переменные yi и yj независимы, то E(yiyj)=E(yi)Е(yj), как в (3.2.12).
3.5. Покажите, что если переменные yi и yj независимы, то sij=0, как в (3.2.13).
3.6. Покажите, что Е(х+у)=Е(х)+Е(у), как в (3.3.2).
3.7. Покажите, что D(y)=E(yyT)–yyT, как в (3.3.8).
3.8. Покажите на примере применение формулы Pr=Ds–1SDs–1 из (3.4.3) при р=3.
3.9. Используя выражение (3.3.5), покажите, что С(v)=С =
= , как в (3.5.2).
, как в (3.5.2).
Вместе с этой лекцией читают "Часть 13".
3.10. Рассмотрим четыре вектора у, х, v и w случайных переменных размеров kx1 и четыре матрицы A, B, C и D размеров hxk некоторых численных значений. Найдите ковариационную матрицу С(Ay+Bx, Cv+Dw).
3.11. Пусть уT= [y1, y2, y3] - вектор случайных переменных с вектором средних y= и матрицей ковариаций S=
и матрицей ковариаций S= .
.
- Пусть x=2y1–3y2+y3. Найдите E(x) и D(x).
- Пусть x1=y1+y2+y3 и x2=3y1+y2–2y3. Найдите E(x) и C(x), где xT=(x1, x2).
3.12. Пусть у - вектор случайных переменных с вектором средних y и матрицей ковариаций S, как дано в упражнении 3.11, и определим вектор wT= [w1, w2, w3] следующим образом:
w1=2y1–y2+y3
w2=y1+2y2–3y3
w3=y1+y2+2y3.
- Найдите E(w) и C(w).
- Найдите С(x, w), используя определённый в упражнении 3.11 вектор x.





















