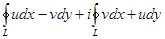Интеграл от функции комплексной переменной
Лекция 4
Интеграл от функции комплексной переменной.
|
| Рассмотрим кусочно-гладкую дугу АВ. Введем разбиение дуги точками А=z0, z1….zk-1, zk, … zn =B. На каждом элементе дуги zk-1, zk отметим точку |
Построим интегральную сумму  . Введем интеграл от функции комплексной переменной по дуге АВ как предел интегральной суммы при неограниченном измельчении разбиения.
. Введем интеграл от функции комплексной переменной по дуге АВ как предел интегральной суммы при неограниченном измельчении разбиения.
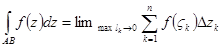
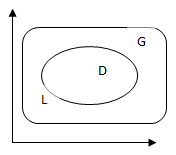
Теорема существования. Пусть функция f(z) непрерывна в области G. Пусть кусочно-гладкая дуга L принадлежит области G. Тогда интеграл 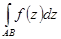
Рекомендуемые материалы
существует как предел интегральных сумм 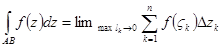
Причем предел этот не зависит:
- от выбора способа разбиения дуги на элементы, лишь бы дуга представляла собой объединение элементов, и пересечение любых двух соседних элементов было бы точкой или пустым множеством (но никак не дугой конечной длины),
- от выбора точек на элементе разбиения, в которых вычисляются значения функции,
- от способа «измельчения» разбиения, лишь бы выполнялось условие  .
.
Свойства интеграла.
1. Линейность а)  =
=  +
+  , б)
, б)  =
= . Заметим, что первое свойство иногда называют аддитивностью, второе – однородностью. Доказательство проводится через интегральные суммы, как в определенном, кратных и криволинейных интегралах.
. Заметим, что первое свойство иногда называют аддитивностью, второе – однородностью. Доказательство проводится через интегральные суммы, как в определенном, кратных и криволинейных интегралах.
2. Аддитивность по множеству. Пусть  . Тогда
. Тогда  =
= +
+ . Доказательство проводится через интегральные суммы с фиксацией граничной точки дуг на основании теоремы существования так же, как в определенном, кратных и криволинейных интегралах..
. Доказательство проводится через интегральные суммы с фиксацией граничной точки дуг на основании теоремы существования так же, как в определенном, кратных и криволинейных интегралах..
3. «Ориентируемость »  =
= , где –L – та же дуга L, но проходимая в другом направлении. Доказательство основано на том, что для дуги L
, где –L – та же дуга L, но проходимая в другом направлении. Доказательство основано на том, что для дуги L  , а для дуги –L
, а для дуги –L  и проводится через интегральные суммы, как в определенном и криволинейных интегралах..
и проводится через интегральные суммы, как в определенном и криволинейных интегралах..
4. 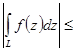
 . Заметим, в правой части неравенства стоит криволинейный интеграл от функции
. Заметим, в правой части неравенства стоит криволинейный интеграл от функции  , принимающей только действительные значения. Доказательство.
, принимающей только действительные значения. Доказательство.  . Переходя к пределу при
. Переходя к пределу при  , получим
, получим 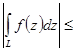
 .
.
5. Пусть 
Доказательство. По свойству 4  .
.
6.  Доказательство. Достаточно показать, что
Доказательство. Достаточно показать, что  и использовать свойство 1б).
и использовать свойство 1б).  . Переходя к пределу при
. Переходя к пределу при  , получим
, получим  .
.
Три формы записи интеграла.
 =
= =
=
= =
=  . Это – 1 форма записи – в виде двух криволинейных интегралов.
. Это – 1 форма записи – в виде двух криволинейных интегралов.
Параметризуем дугу L:  ,
,  .
.
 . Подставляя в первую форму записи, имеем:
. Подставляя в первую форму записи, имеем:
 =
=  .
.
Это – 2 ая форма записи – в виде двух определенных интегралов.
Параметризуем дугу L:z=z(t), 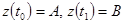
 . Это – третья форма записи – в виде определенного интеграла от комплексно - значной фунции действительной переменной.
. Это – третья форма записи – в виде определенного интеграла от комплексно - значной фунции действительной переменной.
|
| Пример. Вычислить 2) OB: y=x2, 3) OAB 1) Воспользуемся третьей формой записи интеграла, параметризуя дугу OB: (1+i)t, O(0,0) (t=0), B(1,i) (t=1). z2 = (1+i)2 t2, dz = (1+i) dt. = |
2)  .
.
По первой форме записи интеграла
 =
=
= .
.
3) OA: y = 0, dy = 0. AB: x =1, dx = 0. Поэтому 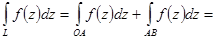

 .
.
Как оказалось, результат во всех трех случаях один и тот же. В чем же здесь дело? Это – случай или закономерность? Ответ на этот вопрос дает интегральная теорема Коши.
Интегральная теорема Коши (для односвязной области).
Пусть G – односвязная область, пусть функция f(z) – аналитическая в G функция, пусть L – кусочно—гладкий контур, принадлежащий области G. Тогда  .
.
Теорему можно сформулировать и так: интеграл от аналитической функции вдоль кусочно-гладкого контура равен нулю.
Доказательство.
|
| Обозначим D – внутренность контура L . Запишем формулу Грина |
Применим к каждому слагаемому в правой части равенства формулу Грина. В первом интеграле примем P = u, Q = -v.

(для аналитической функции выполнены условия Коши – Римана  ).
).
Во втором интеграле примем P = v, Q = u.
 (условие Коши – Римана).
(условие Коши – Римана).
Поэтому  .
.
Следствие. Пусть L1, L2 – две кусочно-гладких дуги в односвязной области G, соединяющие точки A, B. Пусть функция f(z) – аналитическая в области G. Тогда  =
=  .
.
Можно дать словесную формулировку: интеграл от аналитической функции в односвязной области вдоль кусочно-гладкой дуги не зависит от формы дуги, а зависит только от начальной и конечной точек дуги.
Доказательство. Образуем контур  . По интегральной теореме Коши
. По интегральной теореме Коши
 . Но
. Но  . Следовательно,
. Следовательно,  .=
.=  .
.
Поэтому результат в рассмотренном выше примере не случаен.
Очень важный пример. Вычислить интеграл  , где n – целое число, контур
, где n – целое число, контур  - окружность с центром в точке
- окружность с центром в точке  радиусом
радиусом  .
.
Покажем, что точки z на контуре можно описать уравнением
можно описать уравнением  ,
,  ,
,  - действительное число. В самом деле,
- действительное число. В самом деле,  , так как
, так как  . Таким образом, контур
. Таким образом, контур  - это геометрическое место точек комплексной плоскости, расположенных на расстоянии
- это геометрическое место точек комплексной плоскости, расположенных на расстоянии  от точки
от точки  - окружность с центром в точке
- окружность с центром в точке  радиусом
радиусом  .
.
Если  , то подынтегральная функция – аналитическая внутри контура
, то подынтегральная функция – аналитическая внутри контура  . Тогда по интегральной теореме Коши
. Тогда по интегральной теореме Коши  = 0.
= 0.
Пусть  . Так как точка z лежит на контуре
. Так как точка z лежит на контуре  , то
, то  ,
,  . Перейдем к переменной
. Перейдем к переменной  . Пусть
. Пусть  .
.
 =
= 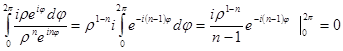
по периодичности экспоненты.
Пусть  . Тогда
. Тогда
 =
= .
.
Вывод.  =
= .
.
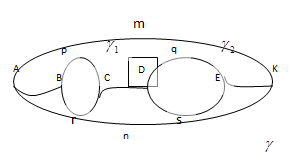
Интегральная теорема Коши для многосвязной области.
Пусть кусочно-гладкие контуры  лежат внутри контура
лежат внутри контура  и вне друг друга. Пусть
и вне друг друга. Пусть  - аналитическая функция в области между контурами и на самих этих контурах. Тогда
- аналитическая функция в области между контурами и на самих этих контурах. Тогда  .
.
|
| Соединим контуры линиями AB, CD, EK. По интегральной теореме Коши интегралы по контуру AbpCDqEKmA и по контуру AnKEsDCrBA равны нулю. Представим эти интегралы как сумму интегралов по составляющим контуры дугам и сложим эти интегралы, сокращая интегралы по одним и тем же дугам в разных направлениях |
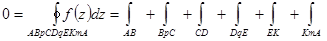
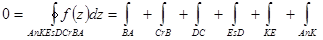
Складывая интегралы, получим
 . Отсюда имеем
. Отсюда имеем
 . Теорема доказана для случая n = 2. Для n > 2 доказательство аналогично.
. Теорема доказана для случая n = 2. Для n > 2 доказательство аналогично.
Следствие 1. В условиях теоремы при n = 1 будет  . Поэтому, если в какой-либо точке нарушается аналитичность функции, то интеграл может быть взят по любому кусочно-гладкому не самопересекающемуся контуру, охватывающему эту точку, мы получим один и тот же результат.
. Поэтому, если в какой-либо точке нарушается аналитичность функции, то интеграл может быть взят по любому кусочно-гладкому не самопересекающемуся контуру, охватывающему эту точку, мы получим один и тот же результат.
Следствие 2. Если кусочно-гладкий контур  один раз охватывает некоторую точку,
один раз охватывает некоторую точку,  .а контур L n раз охватывает эту точку, то в условиях теоремы
.а контур L n раз охватывает эту точку, то в условиях теоремы  . Докажите это самостоятельно.
. Докажите это самостоятельно.
Интеграл с переменным верхним пределом.
Введем интеграл с переменным верхним пределом  . Ясно, что эта запись имеет смысл, если интеграл не зависит от дуги, по которой производится интегрирование, а зависит только от начальной и конечной точек дуги.
. Ясно, что эта запись имеет смысл, если интеграл не зависит от дуги, по которой производится интегрирование, а зависит только от начальной и конечной точек дуги.
Теорема о производной интеграла по переменному верхнему пределу.
Пусть
- функция  непрерывна в односвязной области G,
непрерывна в односвязной области G,
- 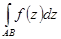 вдоль любой кусочно-гладкой дуги AB, принадлежащей G, не зависит от формы дуги, а зависит только от значений функции в точках A, B.
вдоль любой кусочно-гладкой дуги AB, принадлежащей G, не зависит от формы дуги, а зависит только от значений функции в точках A, B.
Тогда  .
.
Доказательство.
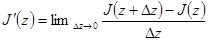 .
.
 ,
, 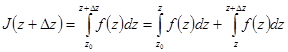
Такая запись оправдана тем, что дугу, соединяющую точки z0 и z +  z, можно провести через точку z, так как интеграл не зависит от формы дуги. На том же основании выберем дугу, соединяющую точки z и z +
z, можно провести через точку z, так как интеграл не зависит от формы дуги. На том же основании выберем дугу, соединяющую точки z и z +  z, отрезком
z, отрезком  прямой линии, тогда
прямой линии, тогда  ,
,  . Заметим, что
. Заметим, что  (свойство 6 интеграла). Надо доказать, что
(свойство 6 интеграла). Надо доказать, что 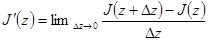
 .
.
Оценим 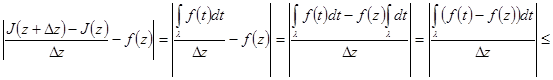
(По непрерывности функции 
 . Точка t лежит на отрезке
. Точка t лежит на отрезке  , соединяющем точки z и z +
, соединяющем точки z и z +  z, поэтому
z, поэтому  .)
.)
 (использованы свойства 4, 6 интеграла).
(использованы свойства 4, 6 интеграла).
Следовательно,  .
.
Поэтому  . Теорема доказана.
. Теорема доказана.
Функция Ф(z) называется первообразной для функции f(z), если  .
.
Следствие. По теореме о производной интеграла с переменным верхним пределом, он является первообразной для подынтегральной функции.
Теорема. Пусть Ф1(z), Ф2(z) – две первообразные для функции f(z), тогда
Ф1(z) = Ф2(z) + С (С- константа).
Доказательство. Обозначим g(z) = Ф1(z) – Ф2(z). g’(z) = Ф1’(z) – Ф2’(z) = f(z) – f(z)=0.
Пусть g(z) = u(x,y) + i v(x,y). Тогда  . Отсюда
. Отсюда
 .
.
Лекция "14. Околоствольные дворы" также может быть Вам полезна.
Формула Ньютона – Лейбница.
Пусть справедливы условия теоремы о производной интеграла с переменным верхним пределом. Пусть Ф(z) – первообразная для функции f(z). Тогда
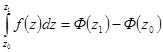
Доказательство.  по теореме о производной интеграла с переменным верхним пределом – первообразная для функции f(z). Поэтому J(z)=Ф(z)+С.
по теореме о производной интеграла с переменным верхним пределом – первообразная для функции f(z). Поэтому J(z)=Ф(z)+С.
J(z0) = 0 = Ф(z0) + C, отсюда С = - Ф(z0). Тогда J(z1) = Ф(z1) + С = Ф(z1) - Ф(z0).



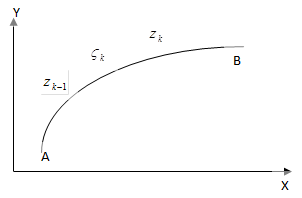
 Обозначим
Обозначим  длину элемента дуги zk-1, zk . Рассмотрим непрерывную на дуге АВ и в некоторой ее окрестности функцию комплексной переменной
длину элемента дуги zk-1, zk . Рассмотрим непрерывную на дуге АВ и в некоторой ее окрестности функцию комплексной переменной  .
.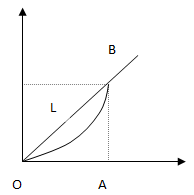
 по трем различным дугам : 1) OB: y=x,
по трем различным дугам : 1) OB: y=x, =
=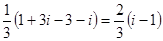
 . Представим интеграл
. Представим интеграл  в первой форме записи через два криволинейных интеграла
в первой форме записи через два криволинейных интеграла