Решение обыкновенных дифференциальных уравнений операционным методом

Решение обыкновенных дифференциальных уравнений

операционным методом

     Пусть дано неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами

                                                                                         (3.25)

и заданы начальные условия       ,

                                                                                                            (3.26)

то есть сформулирована задача Коши.

     Операционный метод решения дифференциальных уравнений базируется на том,  что искомая функция    и  правая  часть   рассматриваются как оригиналы,  и к уравнению (3.25) применяются теоремы дифференцирования и линейности.

     Пусть     , тогда

Рекомендуемые материалы

     ,                                              (3.27)

     Применяя к уравнению (3.25) теорему  линейности,  с  учетом соотношений (3.27) получим

                                        (3.28)

     Алгебраическое уравнение ( 3 .28) называется 2изображающим или операторным уравнением.

     Разрешая его относительно  , находим изображение искомого решения

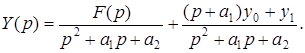
     Далее следует выполнить обратное преобразование Лапласа методами,  указанными  выше,  и  найти соответствующий изображению  оригинал  , который и будет решением задачи Коши (3.25)- (3.26).

     Замечание. Достоинство  операционного  метода  решения   по сравнению  с классическим методом решения неоднородных дифференциальных уравнений состоит в том,  что начальные условия автоматически ( естественным образом в процессе преобразований )  входят в изображающее уравнение. Поэтому после выполнения обратного преобразования Лапласа сразу получается частное решение  уравнения, удовлетворяющее заданным начальным условиям. Следовательно, при операционном методе не надо искать произвольные постоянные.

     Недостаток метода - трудность обращения преобразования Лапласа, особенно в случае сложной правой части или уравнений высокого порядка.

    Пример. Решить операционным методом уравнение

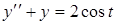
при заданных начальных условиях   ,  .

                              Пусть    ,  

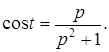
С учетом начальных условий  ,    .

Изображающее уравнение примет вид

Следовательно,

Рекомендуем посмотреть лекцию "1.4 Жесткие магнитные диски".

где

     Для оригинала, соответствующего изображению   воспользуемся теоремой дифференцирования изображения:

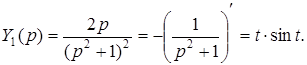
     Изображение  ,  является  табличным.  Ему  соответствует оригинал  . Следовательно,