Уравнения, не содержащие явно искомой функции и ее производных до порядка k-1 включительно

Уравнения, не содержащие явно искомой функции

и ее производных до порядка k – 1 включительно.

Это уравнения вида: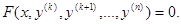

В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:

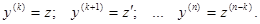
Тогда получаем: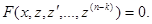

            Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:

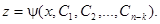
Делая обратную подстановку, имеем:

Рекомендуемые материалы

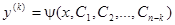
Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:

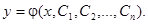
            Пример. Найти общее решение уравнения .

Применяем подстановку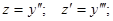

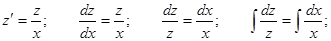
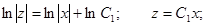
1.2 Политическая борьба в Болгарин в 1944-1948 гг. - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Произведя обратную замену, получаем:

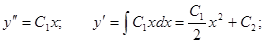
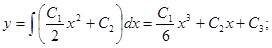
Общее решение исходного дифференциального уравнения:

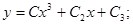
            Отметим, что это соотношение является решением для всех значений переменной х кроме значения х =0.