Квантование непрерывных сигналов

Квантование непрерывных сигналов и теорема прерывания

Процедура преобразования сигнала непрерывного времени x(t) к дискретному (квантованному по времени) виду называется квантованием (рис. 5.4). Такая процедура отражает как реальные процессы, происходящие в цифровых системах управления, так и математические операции, использующиеся в различных сферах теории информации.

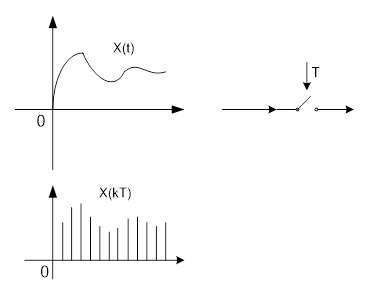
Рис. 5.4. Квантование непрерывного сигнала

В результате квантования получается импульсная последовательность

x(kT) (решетчатая функция), которая при t = kT совпадает с исходным сигналом:

                                   ,

а в другие моменты времени она не определена. Потеря информации при квантовании зависит от величины интервала квантования Т или частоты квантования

                                        .

Выбор интервала Т обычно осуществляется из соображений теоретической

Рекомендуемые материалы

возможности восстановления исходного сигнала по полученой в результате квантования импульсной последовательности (дискретной выборке), что отражает содержание известной теоремы прерывания (теоремы Котельникова – Шеннона).

         Рассмотрим задачу нахождения сигнала x(t) по известной решетчатой функции x(kT), полагая, что спектр сигнала x(t) ограничен частотой .

Тогда в соответствии с теоремой прерывания, точное восстановление функции x(t) теоретически возможно при условии, что частота квантования

Вам также может быть полезна лекция "Критерии качества интерфейса (продолжение)".

более чем в 2 раза превосходит наибольшую частоту :

                              ,

а для интервала квантования выполняется

                              .

Приведенный результат широко используется в задачах идентификации динамических систем и дискретизации непрерывных моделей.