Свойства Z-преобразования

ЛЕКЦИЯ № 3

СВОЙСТВА Z- ПРЕОБРАЗОВАНИЯ.

План лекции:

1.Свойства линейности.

2.Смещение аргумента решетчатой функции.

3.Изображение разностей.

4.Свертка оригиналов.

5.Начальное и конечное значения решетчатой функции.

При использовании Z-преобразования важную роль играют теоремы, устанавливающие связь между операциями с оригиналами и изображениями. Приведем формулировки основных теорем:

Рекомендуемые материалы

Теорема 1     Линейность Z-преобразования.

Z.

Теорема 2      Смещение аргумента решетчатой функции.

                       (теорема о запаздывании, упреждении.)

-запаздывание на -тактов.

-упреждение на -тактов.

Рассмотрим преобразование:

Z.

Введем обозначение:    , тогда: 

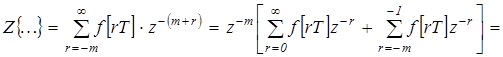
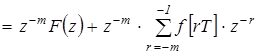
если значение решетчатой функции равно 0 при отрицательных значениях аргумента, то:

Z.

Аналогично для случая упреждения:

.

Теорема 3      Изображение разностей. 

Первая обратная разность:

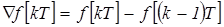
На основании предыдущей теоремы:

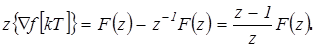
Для обратной разности m-ого порядка:

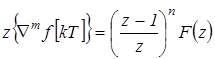
Для прямой разности:

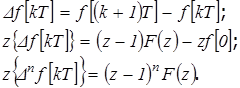
Последнее выражение записано в предположении, что.

Теорема 4    преобразование произведения изображений непрерывной и решетчатой функции.

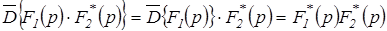
Теорема 5        Конечное значение решетчатой функции.

             Предварительно определим сумму ординат решетчатой функции:

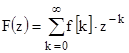
Положим  , отсюда: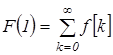 

Далее, учитывая, что

,

найдем сумму ординат решетчатой функции:

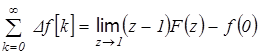
с другой стороны:

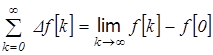
Приравнивая правые части уравнений получим:

.

Теорема 6         Начальное значение решетчатой функции.

Напомним, что первая прямая разность определяется выражением:

.

Тогда:

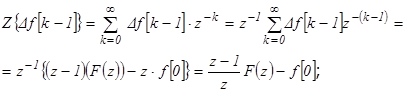
Рассмотрим теперь предел выражения:

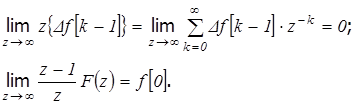
Приведенные зависимости являются аналогами для нахождения конечного и начального значений непрерывной функции  по ее изображению Лапласа:

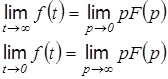
Теорема 7         Свертка решетчатой функции.

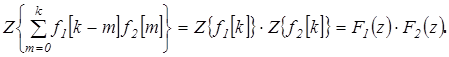
Наряду с прямым дискретным преобразование при анализе цифровых систем управления широкое применение находит и обратное дискретное преобразование Лапласа определяемое формулой:

,                                        (3.1)

где  -абсцисса абсолютной сходимости оригинала .

Замена   преобразует отрезок интегрирования в плоскости “P” в окружность плоскости  “Z”. При этом выражение (3.1) трансформируется в формулу обращения Z-преобразования:

                                                           (3.2)

где:       .

Пояснения:

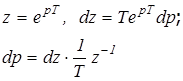
Выражения (3.1), (3.2) достаточно сложные и непосредственно применяются редко, т.к. существуют более простые способы вычисления решетчатых функций.

Применяя для вычисления контурного интеграла (3.2) теорию вычетов, получим:

           (3.3)

где -особые точки подынтегрального выражения. Обычно F(z)-дробно-рациональная функция, и тогда выражение (3.3) может быть доведено до конечных зависимостей:

;      ; .

Обратное Z-преобразование можно вычислять также и методом степенных рядов. Запишем формулу Z-преобразования в виде:

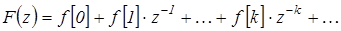
Тогда вычисление обратного Z-преобразования сводится к определению коэффициентов разложения F(z) в ряд Лорана.

Пример:  Задано, найти образующую решетчатую функцию.

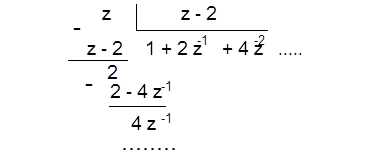Решение получим делением многочлена на многочлен:

Ещё посмотрите лекцию "Условия для взрыва газа" по этой теме.

Таким образом, ; и, соответственно,

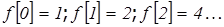
Другой вариант решения заключается в применении теории вычетов:

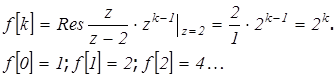
Преимущество метода степенных рядов заключается в том, что при этом не требуется находить полюса F(z). Если F(z)-дробно-рациональная функция, то значения  находятся делением полинома числителя на полином знаменателя.(см. пример).

Недостаток метода состоит в том, что вычисления ведутся по рекуррентной процедуре. Кроме того, алгоритм деления многочлена при реализации на ЭВМ может приводить к накоплению вычислительных ошибок.