Выбор подходящих систем с поведением

                                                                                                 Лекция 14

4.14 Выбор подходящих систем с поведением

            Дана система данных D с полностью упорядоченным параметрическим множеством и с наибольшей допустимой маской М, совместимой с D; требуется определить все системы с поведением, удовлетворяющие требова­ниям согласованности, детерминированности и простоты, причем требование согласованности более приоритетно, чем остальные два.

            Любая наибольшая допустимая маска М содержит набор корректных масок, каждая из которых является подмножеством М. Для каждой маски может быть опре­делена функция поведения, хорошо согласующаяся с данными, с помощью разреженной вы­борки данных. Однако на практике достаточно провести выборку только для маски М. Функции поведения для ее подмасок могут быть получены вычислением проекций функции по­ведения соответствующей маски М.

   Для заданной функции, определенной через полные состоя­ния неких выборочных переменных, любая из ее проекций также является функцией поведения, соответствующей , основанной на определенном подмножестве выбо­рочных переменных. Пусть — выборочные перемен­ные, через которые определяются состояния— маска, через которую выбираются значения выборочных переменных. Пусть  — проекция, где подмножество множестваиденти­фикаторов выборочных переменных, т. е.. Тогда

 (4.55)

так что

(4.56)

Рекомендуемые материалы

где а — некая агрегирующая функция, определяемая характером функции. Например,

(4.57)

где — распределение вероятностей.

Будем в контексте любой конкретной задачи черезобозна­чать функцию поведения для наибольшей приемлемой маски . Через  будем обозначать функции поведения для ее различных осмысленных подмасок , каждая из которых свя­зана с множествомидентификаторов выборочных пере­менных.

За исключением очень небольших наборов данных, с точки зре­ния вычислений проще определять функции поведения с помощью проекций, а не через выборки данных. Таким образом, лучше производить выборку только однажды для наибольшей приемле­мой маски, а затем определять функции поведения для всех содер­жательных подмасок как соответствующие проекции.

Пример 4.3. Определим проекцию вероятностной функции по­ведения, приведенной на рис. 4.5,а  для . Применив форму­лу (4.57) для вероятностной функции, получим:

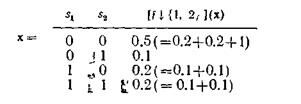
4.15 Упорядочение по сложности и нечеткости

Для заданной системы данных D и наибольшей допустимой маски М требование соответствия приводит к ограниченному множеству

(4.58)

содержащему по одной системе с поведением для каждой осмыс­ленной маски ; пусть для удобства . Следующим шагом решения рассматриваемой задачи должно быть вычисление степеней недетерминированности и сложности для всех систем из множества.

Как было показано  степень недетерминированности задается соответствующей мерой порождающей нечеткости, опре­деляемой для вероятностных систем шенноновской энтропией.

Что касается меры сложности, то тут возможно много вариан­тов. Возьмем для примера простую, но содержательную меру, которую часто используют в АСНИ  — размер (мощность) маски.

Пусть — значения соответствующих порождающих нечеткостей для систем с поведением из ограниченно­го множества  Поскольку любая система однозначно иденти­фицируется своей маской М, мощность которой  задает ее сложность, статус системы в смысле порождающей нечеткости и сложности удобно описывать парой .

Численное упорядочение масок , идентифицирующих системы из по их мощности, задает упорядочение сложности  на мно­жестве . Численное упорядочение значений определяет упо­рядочение по нечеткости  на множестве Y_r. В то время, как упорядочение по сложности полностью определяется самими мас­ками, упорядочение по нечеткости может быть определено только после оценки масок. Для любого множества порождающих масок мы можем определить частичное упорядочение  тогда и только тогда, когда

 (4.59)

(илидля направленных систем), которое мы будем называть упорядочением подмасок.

Пример упорядоченности по сложности и упорядоченности подмасок для наибольшей допустимой маски М при n=3 и приведен на рис. 3.10. При этом предполагается, что данные по­рождаются слева направо. Все содержательные подмаски изобра­жаются своими матрицами и помечены в левом верхнем углу свои­ми идентификаторами i. По сложности они разбиты на четыре группы. Маски с одинаковой сложностью расположены на одном уровне. Например, маски с идентификаторами 2—7 образуют группу со сложностью 5, маски 8—19 — другую группу со слож­ностью 4 и т.д. С точки зрения упорядоченности по сложности любая маска некоторого уровня является непосредственным пре­емником любой маски ближайшего более высокого уровня и не­посредственным предшественником любой маски ближайшего более низкого уровня. На рис. 4.7 стрелками показано упорядочение по подмаскам. Из этого примера видно, что упорядочение по сложности — это связное квазиупорядочение (рефлексивное и транзитивное отношение, определенное для любой пары систем).

Упорядочение по подмаскам — это частичное упорядочение, но решетки оно не образует. Однако оно представляет собой на­бор решеток по одной для каждого множества порождаемых вы­борочных переменных (в нашем примере это крайние правые эле­менты масок).

Упорядочение по нечеткости связное, но из-за того, что не­сколько разных систем могут иметь одинаковую порождающую нечеткость, это отношение не является антисимметричным. Сле­довательно, в общем случае это связное квазиупорядочение, ко­торое в некоторых частных случаях оказывается полным упоря­дочением.

Таким образом, на множестве определены два связных ква­зиупорядочения — по сложности и по нечеткости. Поскольку для рассматриваемого типа задач требуется, чтобы и сложность, и порождающая нечеткость систем во множестве решений Y_Q была минимизирована, соответствующее объединенное упорядо­чение  определяется следующим образом: тогда и только тогда, когда

 (4.60)

где. Это упорядочение не является связным, поскольку пары , для которых иили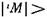 (подобные пары, разумеется, могут существо­вать), несравнимы. Оно также неантисимметрично, так как не исключена возможность того, что

,(4.61)

для некоторых . Следовательно, объединенное упорядоче­ние — это общего вида квазиупорядочение (рефлексивное и транзитивное отношение) на .

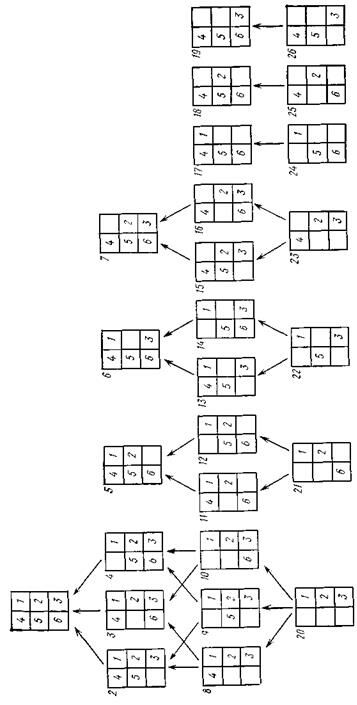
Рис. 4.7 Содержательные маски для  классифицированные согласно упорядоченности по сложности подмасок

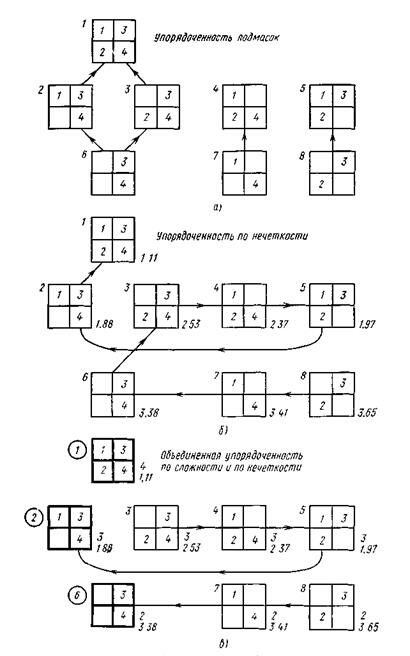
Рис. 4.8

Теперь множество решений можно определить как множе­ство всех систем из , которые или эквивалентны, или несравни­мы относительно объединенного упорядочения (4.60). Две систе­мы из , скажем системы и , несравнимы в смысле объ­единенного упорядочения, если выполнено одно из следующих условий:

(а)  более сложна и более детерминирована, чем или  менее сложна и менее детерминирована, чем. Формально

(4.62)

Системы из множества решений  будем называть подходящи­ми системами с поведением для рассматриваемого типа задач.

Пример 4.4. Чтобы пояснить различные вопросы, изучаемые в данном разделе, рассмотрим некоторую систему данных. Определим все подходящие в смысле (4.62) системы с поведением для этой си­стемы данных в предположении, что необходимо  получить описания вероятностных систем с поведением и использовать их для предсказания.

Предположим сначала, что . Тогда имеется восемь содержательных масок, которые вместе с их упорядочением подмасок и указанием трех уровней сложности изображены на рис. 4.8,а. После выполнения исчерпывающей выборки для наи­большей приемлемой маски по определенной формуле, по частотам N(c) вычисляются вероятности , а порождающая нечеткость вычисляется или по формуле (4.48). Если для вычисления вероятностей используется формула (4.31), то порождающая не­четкость равна 1.11. Затем для остальных семи содержательных масок по формуле (4.57) определяются соответствующие проек­ции и вычисляются их порождающие нечеткости. Результаты этих вычислений показаны на рис. 4.8,б (в правом нижнем углу масок). На рис. 4.8,б также изображено упорядочение ма­сок по нечеткости. В этом при­мере упорядочение является полным, поскольку значения нечеткости у всех разные. Объ­единенное упорядочение по сложности и нечеткости (3.60) изображено на рис. 4.8,в. Как мы видим, минимальными с точки зрения объединенного упорядочения являются маски

Бесплатная лекция: "11 Ввод и вывод" также доступна.

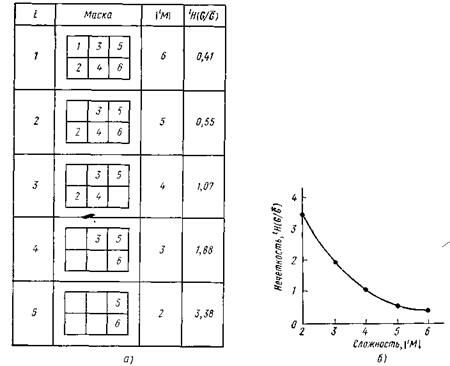
Рис. 4.9 Подходящие системы с поведением из примера 4.4

с идентификаторами  1, 2, 6. Следовательно,. Предположим теперь, что =3. Тогда согласно формуле (4.36) имеется 40 содержательных масок. После их обработки, аналогичной обработке для случая , мы получим пять подходящих систем с поведением, маски которых, значения сложно­сти и порождающие нечеткости приведены на рис. 4.9,а. Остав­шиеся 35 масок хуже с точки зрения их сложности, как и с точки зрения четкости, и, следовательно, их вовсе не нужно рассматри­вать. Рис. 4.9,а — это типичный пример ответа АСНИ. При соответствующих запросах могут также вы­даваться различные дополнительные характеристики, множества решений, такие, как график зависимости нечеткости от сложно­сти, изображенный на рис. 4.9,б.

Описанный здесь поиск подходящих систем с поведением мо­жет быть реализован самыми разными способами. Основной принцип заключается в том, что содержательные маски получа­ются с помощью некоторого алгоритма из наибольшей приемле­мой маски в порядке уменьшающейся сложности. Среди масок одинаковой сложности выбираются только маски с минимальной порождающей нечеткостью. При этом если значение этой мини­мальной нечеткости меньше или равно значению нечеткости для предшествующего уровня сложности, то все ранее принятые си­стемы отбрасываются. В результате применения этой процедуры у нас остаются только подходящие системы.

К.Р. № 14

Для некоторой системы данных упорядочить маски по сложности и нечеткости.