Меры нечеткости

Лекция 13

4.12 Меры нечеткости

            Степень недетерминированности должна измеряться обобщенной нечеткостью, сопутствующей порождению данных. А значит, она должна быть определена через порождающие функ­ции поведения  и  для нейтральных и направленных систем с поведением. Если эти функции представляют собой функции распределения вероят­ностей, то мера обобщенной нечеткости хорошо известна — это шенноновская энтропия

,(4.37)

Она измеряет нечеткость в единицах, называемых битами.

Если предположить, что любое конечное множество X рассма­триваемых альтернативных выходных значений характеризуется определенным распределением вероятностей, то удобнее упростить обозначения и писать   вместо  .

Легко видеть, что

,(4.38)

Рекомендуемые материалы

Нижняя граница  достигается в том случае, когда вероятности всех выходных значений, за исключением одного, равны 0; верхняя граница достигается тогда, когда вероятности всех событий одинаковы, т. е. равны . Отношение энтропии к ее верх­ней границе

,(4.39)

называется нормализованной энтропией; понятно, что

, (4.40)

В нашем случае множествами выходов являются множества  а распределения вероятностей представляются функция­ми поведения , определяемыми соответственно фор­мулами  (4.11),  (4.17), (4.27),  (4.30). Для упрощения записи опу­стим индексы В и GB, а также знак  ^ .   Таким образом,

,(4.41)

обозначают вероятности, определяемые соответственно формула­ми (4.11), (4.17), (4.27), (4.30); смысл любого из этих обозначе­ний однозначно определяется заключенными в скобки аргументами. Кроме того, определим безусловные вероятности

, (4.42)

где  указывает на то, что  является подмножеством состояния с (подсостоянием с); формально, если

,(4.43)

,(4.44)

то  тогда и только тогда, когда   для   всех  .  Для направленных систем безусловные вероятности    вычисляются по немного измененной формуле

, (4.45)

Условные вероятности, характеризующие процесс порождения данных, связаны с основными (совместными) и безусловными ве­роятностями следующим образом:

;(4.46)

.(4.47)

Первая формула описывает эту связь для    нейтральных, а вто­рая — для направленных систем.

4.13 Методы вычислений нечеткости

При заданной порождающей маске для нейтральной системы, через которую определяются множества состояний  генерируемых и генерирующих выборочных переменных, порождающая нечеткость  определяется как средняя    нечеткость, базирующаяся на    вероятностях , взвешенных    вероятностями  порождающих условий:

. (4.48)

Это значение определяет степень недетерминированности данной нейтральной порождающей системы с поведением.

Для направленных систем порождающая нечеткость   вычисляется по формуле

,(4.49)

которую можно непосредственно применять в том случае, когда можно и имеет смысл определять вероятности, т. е. когда направленная система получена из нейтральной. Если мы не рас­полагаем вероятностями состояний элементов множества Е или эти вероятности несущественны, тогда в качестве базовых вероятно­стей берутся вероятности  [аналог вероятностей f(c) для нейтральных систем], исходя из которых вычисляются остальные необходимые вероятности. В этом случае нечеткость  вычисляется формуле (4.50)

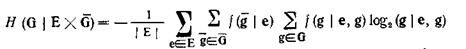где    вероятност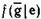и  и 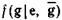  вычисляются по заданным вероятностям  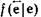согласно формулам (4.45) и (4.47).

 Формулы (4.48), (4.49) и (4.50) можно заменить другими, более удобными для вычисления. Например, уравнение (4.48) можно модифицировать следующим образом:

,(4.51)

Таким образом,  можно вычислить, не используя условные вероятности, по формуле

 (4.52)

Точно так же уравнения (3.49) и (3.50) можно заменить соответ­ственно уравнениями

(4.53)

Максимальное значение порождающей нечеткости любого типа равно; следовательно, нормализованная порождающая нечеткость получается делением порождающей нечеткости на ее максимальное значение. Например,

  ,(4.54)

Пример 4.2. На рис. 4.5,а показана    вероятностная    функция поведения  для четырех выборочных переменных  каждая с двумя состояниями — 0 и 1. Состояния с нулевой веро­ятностью в таблице не приводятся. Выборочные переменные опре­делены через две базовые переменные с помощью маски, изображенной на рис. 3.7,а. Поскольку выборочные переменные  суть сдвиги одной и той же базовой переменной, распре­деления вероятностей их состояний должны быть одинаковы; они и в самом деле одинаковы; оба имеют вероятности 0.7 и 0.3 соот­ветственно для состояний 0 и 1. Аналогично переменные (сдвиги) имеют одинаковое распределение вероятностей: 0.6 и 0,4 соответственно для состояний 0 и 1. Следовательно, для дан­ной маски приведенная функция распределения вероятностей яв­ляется корректной функцией поведения.

Если данная система интерпретируется как нейтральная, ее порождающая нечеткость может быть вычислена по формуле (4.52). Для первого члена формулы мы имеем

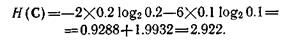
Значение второго члена зависит от порядка порождения и от со­ответствующей маски. На рис. 4.5,в и г показаны два возможных порядка порождения. Для порождения слева направо имеем

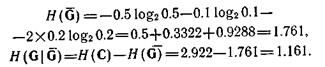
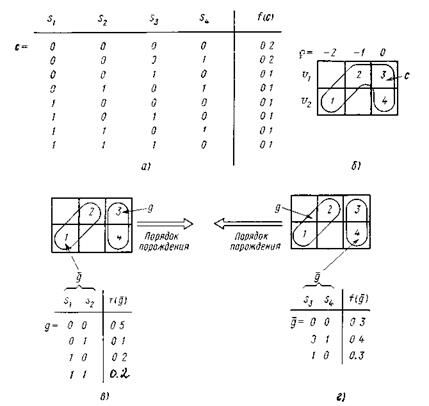
Рис. 4.5 Вероятностная нейтральная система

Для другого порядка порождения (рис. 4.5,г) мы получим

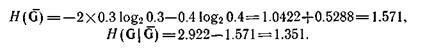
Следовательно, нам можно выбрать один из двух порядков по­рождения; первый порядок предпочтительнее, так как имеет более низкую порождаемую нечеткость. Поскольку в данном примере  , то нормализованные значения вычислительных по­рождающих нечеткостей получаются делением их на два.

В некоторых случаях применим только один порядок порож­дения. Если, например, параметром является время, то в каждом случае имеет смысл только один из порядков, определяемый целью использования системы с поведением. Если она использу­ется для предсказания, то состояния должны порождаться в по­рядке возрастания времени (слева направо); если же она исполь­зуется для ретроспекции, то состояния должны порождаться в порядке убывания времени. В данном примере, если парамет­ром является время, то оказывается легче предсказывать буду­щие состояния системы, чем определять прошлые.

Предположим теперь, что   интерпретируется  как входная переменная и что по функции поведения на рис. 4.5,а определена соответствующая направленная система. Теперь для вычисления порождающей нечеткости можно воспользоваться формулой (4.53). Нечеткость  уже была вычислена раньше;зависит от порядка порождения. В любом случае множество Е представляется состояниями переменныхпредставляется или состояниями (в порядке возрастания параметра) или со­стояниями (в порядке убывания параметра). В первом случае нечеткостьсвязана с переменными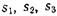

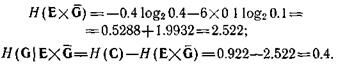
Во    втором    случае она    представляет    нечеткость  переменных:

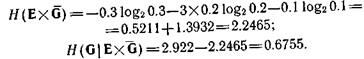
Таким образом, снова оказывается, что предсказывать    будущие состояния легче, чем определять прошлые.

Предположим теперь, что мы не располагаем никакой инфор­мацией относительно входной переменной или что эта инфор­мация несущественна (например, в том случае, когда контро­лируется пользователем). Тогда все вычисления должны прово­диться для приведенных на рис. 4.6,а условных вероятностей. Как показано на этом рисунке, список вероятностей раз­битна четыре части, соответствующие разным состояниям е. Нечеткости для каждого состояния также приведены на рис. 4.6,а. Здесь же показано разбиение маски на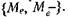

Ситуация при порождении состояний слева направо, включая значения для каждого состояния е, показана на рис. 4.6,в.

Из формулы (4.53) получим

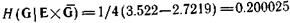
Другой порядок порождения изображен на рис.  4.8,г. Для него имеем

8 Выражения - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

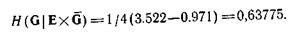
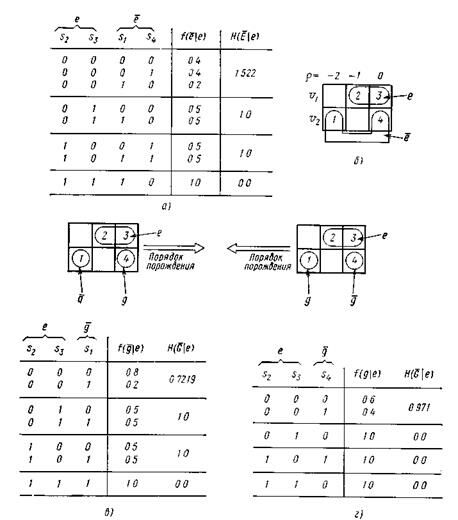
Рис. 4.6 Вероятностная направленная система

К.Р. № 13

Рассчитать порождающую нечеткость для случая направленной и нейтральной системы с поведением. Рассмотреть оба порядка порождения.