Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

Глава 6.

Магнитные цепи при постоянной магнитодвижущей силе (МДС).

Магнитная цепь (МЦ) – часть электротехнического устройства, предназначенного для создания в определенном месте пространства магнитного поля требуемой интенсивности и направленности. Магнитные цепи составляют основу практически всех электротехнических устройств и многих измерительных приборов.

В составе МЦ имеются элементы, возбуждающие магнитное поле (одна или несколько намагничивающих обмоток или постоянные магниты) и магнитопровод, выполненный в основном из ферромагнитных материалов. Использование ферромагнетиков обусловлено их способностью многократно усиливать внешнее (по отношению к ним) магнитное поле, создаваемое намагничивающими обмотками или постоянными магнитами. Ферромагнетики отличает высокая магнитная проницаемость по сравнению с окружающей средой, что дает возможность концентрировать и направлять магнитные поля.

На рис. 1.1 в качестве примера представлены МЦ некоторых электромагнитных устройств: а – машин постоянного тока, б – электромагнитного реле, в – трансформатор, г и д – тормозных электромагнитов, е – магнитоэлектрического измерительного прибора. Цифрой 1- обозначены ферромагнитные части магнитопроводов, 2 – воздушные зазоры, 3 – намагничивающие катушки, 4 – постоянный магнит.

МЦ с постоянной МДС называются цепи, в которых магнитное поле возбуждается постоянными токами намагничивающих обмоток или постоянными магнитами.

При анализе и расчете магнитных цепей пользуются следующими величинами, характеризующими магнитное поле:

1. – вектор магнитной индукции. Характеризует интенсивность и направленность магнитного поля в данной точке пространства. Единица измерения – тесла (1 Тл = ).

2. – вектор напряженности магнитного поля в данной точке. Единица измерения – ампер на метр ( ).

Отношение – абсолютная магнитная проницаемость. Для вакуума, а также для любых неферромагнитных материалов принимается равной m₀= 4π·10^-7 Гн/м; отношение – относительная магнитная проницаемость ( для конкретных ферромагнетиков может доходить до 10⁴ – 10⁶ ).

1. Ф – магнитный поток – поток вектора магнитной индукции через площадь S (рис. 1.2), единица измерения вебер (1Вб=1Тл×1м²)

1.1

Вслучае однородного магнитного поля, когда B=const в любой точке

поля и вектор магнитной индукции ^S (Ða=0), магнитный поток

Ф=B×S 1.2

Расчет магнитной цепи невозможен, если неизвестна основная кривая намагничивания (ОКН) ферромагнетика, используемого в магнитопроводе.

ОКН задается в справочной литературе на электротехнические материалы как зависимость В(Н) либо в табличной форме, либо графически (рис. 1.3).

Отметим, что на участке оа, отношение const. – магнитная цепь не насыщена. При дальнейшем увеличении Н темп увеличения индукции В снижается и прекращается полностью, когда наступает магнитное насыщение материала магнитопровода.

6.1.Законы магнитных цепей.

Наиболее общим законом является закон полного тока. Этот закон устанавливает взаимосвязь между напряженностью магнитного поля и вызвавшим её током.

Формулировка закона:

Л инейный интеграл от вектора напряженности по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром – полному току (I_полн).

При определении полного тока в уравнение закона полного тока со знаком «+» следует включать токи, положительные направления которых связаны с произвольно выбранным направлением обхода правилом правоходового винта.

На рис. 1.4 контур интегрирования пронизывает три отдельных витка с токами I₁, I₂, I₃.

Закон полного тока:

1.3.

Рис. 1.4 Для практических целей наибольший интерес представляет частный случай, когда контур интегрирования проходит внутри обмотки с числом витков w и током I (рис 1.5) В этом случае полный ток .

П роизведение (w×I) называют магнитодвижущей силой (МДС). МДС возбуждает магнитный поток Ф в магнитной цепи подобно тому, как ЭДС возбуждает ток в электрической цепи.

Как и ЭДС, МДС является величиной направленной, ее положительное направление указывается на схеме. Положительное направление МДС w×I принимают совпадающим с поступательным движением правоходового винта, если вращать его по направлению тока в обмотке.

Удобно использовать и другое правило для определения направления МДС обмотки, а именно: если мысленно обхватить правой рукой сердечник, расположив пальцы по направлению тока, то отогнутый большой палец покажет направление МДС (рис 1.6).

6.2.Магнитное напряжение на участке магнитной цепи.

М агнитным напряжением между точками а и b магнитной цепи называют линейный интеграл от вектора напряженности магнитного поля между этими

точками (рис.1.7): 1.4.

Если на участке магнитной цепи =const и совпадает по направлению с элементом пути обхода , то

1.5.

Если принять в внимание, что Н=В/m_а, где m_а – абсолютная магнитная проницаемость, а В=Ф/S, то формулу 1.5 магнитного напряжения U_abM можно представить в виде

U_abM=Ф×R_M , 1.6.

где – магнитное сопротивление.

Выражение 1.6 называют законом Ома для магнитной цепи по аналогии с электрической цепью (поток Ф – аналог тока I, R_M – аналог электрического сопротивления R). Так же, по аналогии с электрической цепью и закон полного тока, представленный в виде

, 1.7

называют вторым законом Кирхгофа для магнитной цепи (алгебраическая сумма магнитных напряжений вдоль любого замкнутого контура равна алгебраической сумме МДС).

6.3.Задачи расчета магнитных цепей.

Существует два типа задач, а именно:

1. прямая задача – по заданному значению потока Ф определяют МДС w×I обмотки;

2. обратная задача - задается значение МДС w×I и требуется определить поток Ф.

В обоих случаях должны быть известны геометрические размеры магнитопровода (длины l и площади поперечных сечений S всех участков магнитопровода), материалы участков и кривые намагничивания.

Для упрощения расчета пренебрегают магнитными потоками рассеяния Ф_р (рис. 1.8) и не учитывают выпучивание магнитного поля в воздушных зазорах, считая площадь сечения воздушного зазора S₀ (рис. 1.8) равной площади поперечного сечения ферромагнитного магнитопровода.

1.Решение прямой задачи.

1.1Неразветвленная магнитная цепь.

Пример подобной цепи представлен на рис. 1.8.

Эту цепь можно разбить на четыре участка, три из которых выполнены из ферромагнитного материала ( например: электротехническая сталь Э2 ), кривая намагничивания которого известна рис 1.9. Четвёртый участок – воздушный зазор.

Характерный признак неразветвлённой магнитной цепи – магнитный поток Ф на всех участках один и тот же (рис. 1.8). Его значение задано в условии задачи. Магнитный поток Ф называется основным. Этот поток замыкается по магнитопроводу в отличие от потока рассеяния Ф_р, силовые линии которого замыкаются вокруг витков катушки по воздуху. Обычно Ф значительно больше Ф_р.

Рис. 1.8

Магнитная проницаемость воздуха m₀=4p×10^-7 Гн/м ничтожно мала по с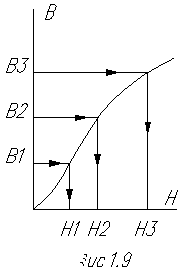 равнению с проницаемостью ферромагнитного магнитопровода и магнитное сопротивление потоку Ф_р несравненно выше, чем для потока Ф (Ф_р<<Ф).

Чтобы использовать при расчете закон полного тока, выберем контур интегрирования, проходящий внутри катушки с числом витков w и совпадающий со средней линией магнитной индукции. Разобьем магнитную цепь на отдельные участки: участок da – длина средней линии магнитной индукции l₁, площадь поперечного сечения S₁, на участке ab длина l₂, площадь поперечного сечения S₂ , на участке cd длина l₃ , площадь поперечного сечения S₃ , на участке воздушного зазора длина l₀ , площадь S₀=S₂.

Пусть S₁> S₀=S₂> S₃ , тогда магнитная индукция по участкам:

, , , .

Учитывая соотношения между площадями сечений, получим B₁<B₂=B₀<B₃. Далее по кривой намагничивания рис. 1.9, определим напряжённость магнитного поля на ферромагнитных участках Н₁ ,H₂, Н3.

Напряженность поля в зазоре рассчитывается по формуле: , где m₀=4p×10^-7 Гн/м – магнитная постоянная.

Так как напряженность поля на каждом из четырех участков постоянна, интегральная формула закона полного тока принимает следующий вид:

1.8

Из этого уравнения определяется МДС w×I. Отметим, что в уравнении 1.8 слева – сумма падений магнитных напряжений на участках магнитной цепи. Уравнение 1.8 можно представить иначе, если заменить магнитные напряжения в левой части уравнения произведениями потока Ф на магнитные сопротивления участков магнитной цепи (формула 1.6) и общий для всех участков поток Ф вынести за скобки, тогда , откуда

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов лекций