3 Глава (1084725), страница 10
Текст из файла (страница 10)
и
максимизирующих или минимизирующих целевую функцию
(3.65)
где ai, Ci — заданные константы.
В формулировании задач линейного программирования требуется, чтобы все переменные были неотрицательными, т. е. хi, > 0, j = 1, 2, ..., п. При таких условиях задача удобна для численного решения.
Задачи линейного программирования в настоящее время хорошо изучены, и решение их сводится к сравнительно простым вычислениям. На многие из них имеются разработанные для ЭВМ типовые программы.
В ряде случаев встречаются задачи нелинейного программирования, целевая функция которых записывается как сумма линейных и нелинейных:
(3.66)
Среди задач нелинейного программирования встречаются такие, в которых ограничения не имеют дискретных переменных. В них функции f(x1, х2, .... xn) непрерывные и выражаются частными производными. Эти задачи иногда называют классическими задачами оптимизации, поскольку решаются классическими методами на основе дифференциального исчисления.
Различают также другой вариант задач нелинейного программирования. Это задачи целочисленного линейного программирования. В этом случае в качестве ограничений выставляют особое требование о целостности переменных значений.
З
адача формулируется следующим образом:
(3.67)
85
Решение большого количества производственных задач методами линейного и нелинейного программирования обеспечивает в строительстве большой экономический эффект, в частности, снижение сметной стоимости в результате оптимизации процессов составляет 3—7%.
Некоторые практические процессы в строительном производстве непрерывно изменяются, особенно те, что связаны с управлением производством. В связи с изменением условий доставки материалов, наличием строительных и дорожных машин, изменением метеорологических и грунтовых условий, наличием бригад разных специальностей практически ежедневно на производстве приходится рассматривать новые ситуации. Таким образом, строительный процесс является динамическим.
Решение ряда практических задач в строительстве с учетом различных ситуационных изменений, особенно в управлении процессом, можно осуществить с помощью метода динамического программирования.
Этот метод в строительстве начали применять лишь в последние годы. Уже известны решения ряда задач, направленных на оптимизацию процессов: при выборе оптимальных составов машин, распределении капиталовложений в строительство в различные периоды, решении технико-экономических задач по реконструкции различных объектов, оценке эффективности развития производственной базы и т. д.
В основу задач динамического программирования положены принципы оптимальности. Оптимальное управление процессом определяется заданной целью и составлением системы в рассматриваемый период времени, независимо от изменившихся условий, которые привели систему в данное состояние.
Ц
елевая функция выражается суммой
(3.68)
где N — общее число интервалов (шагов); u(k) — управляющие воздействия; x(k) — значение координаты в дискретные моменты времени t.
При оптимальном управлении функционал (3.62) должен быть минимизирован или максимизирован. Оптимальный процесс станет известен, если будут найдены значения управляющего воздействия u0, u1, ..., u n-1 во все дискретные моменты времени k = О, 1, .... N—1, имеющие определенные ограничения и минимизирующие (максимизирующие) сумму (3.62).
Чтобы решить задачу динамического программирования, необходимо отыскать минимум (максимум) сложной дискретной функции большого количества переменных..Метод динамического программирования сводит эту задачу к простой — минимизируются простые функции в обратном порядке — от конца к началу процесса.
86
Для исследования оптимизации процессов методами линейного, нелинейного или динамического программирования нет стандартных решений. В каждом конкретном случае применяют свой подход (метод) к решению задачи. Особенно трудны задачи нелинейного и динамического программирования.
Следует иметь в виду, что при решении задач оптимизации строительного производства могут возникнуть случаи, когда вследствие оптимизации какого-либо процесса может ухудшиться другой. Поэтому необходимо соблюдать комплексность решения с учетом всех особенностей процесса и смежных его факторов. Рассматривая задачу по этапам, необходимо анализировать в целом обстановку, которая складывается в результате оптимизации исследуемого процесса.
Одним из методов оптимизации процессов, применяемых в последнее время в строительстве, являются методы, основанные на теории массового обслуживания (ТМО). ТМО имеет целью отыскать оптимальные условия, т. е. обеспечить эффективность работы системы «требование — обслуживание».
Под обслуживанием понимают удовлетворение в потребности какой-либо заявки. Например, погрузка щебня в карьере в автомобили-самосвалы. В этой системе в качестве требования выступает подача под погрузку автомобилей в карьер по заявкам, в качестве обслуживания — погрузка щебня средствами погрузки (экскаваторы, автопогрузчики, транспортеры и др.).
Таким образом, в ТМО система состоит из числа (потока) требований, обслуживающего прибора (аппарата) и выходящего потока.
В зависимости от условий функционирования системы число требований создает очередь на обслуживание. Так, при избытке автомобилей неизбежно возникают простои на погрузку перед экскаватором.
Основными характеристиками ТМО являются:
интенсивность поступления требований или заявок на обслуживание, л интенсивность обслуживания (пропускная способность прибора обслуживания), м.; коэффициент использования системы,
ф = л/м; время ожидания в очереди до обслуживания, t0; длительность обслуживания, t1; время обслуживания в системе, tоб; число требований в очереди, л; математическое ожидание числа требований в системе, nс-
Эти характеристики имеют следующие соотношения:
(3.69)
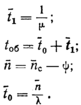
87
Индекс «—» означает, что принимаются средние значения; л, tо, t1,. tоб, n, как правило, принимают случайные значения. Чаще всего распределение времени обслуживания по длительности выражается показательным законом.
В ТМО ф < 1, т. е. интенсивность обслуживания выше интенсивности требования. Тем не менее возникает очередь на обслуживание, поскольку toб по ряду причин величина переменная, а интервал между обслуживанием неритмичен. В результате, несмотря на то что м. > л, возникают очереди.
Задачей ТМО в конечном счете является установление наиболее достоверных зависимостей между интенсивностью потока требований и производительностью (пропускной способностью) прибора, их количеством и эффективностью обслуживания системы.
Показателями эффективности функционирования системы могут быть tо, t1, tоб, приведенная стоимость и др.
Теория массового обслуживания базируется на анализе случайных процессов. При решении тех или иных практических задач в каждом случае принимаются индивидуальные решения.
В
качестве примера рассмотрим случай обслуживания асфальтобетонного смесителя на АБЗ автомобилями-самосвалами. Имеется система «смеситель-автосамосвалы». При обычном расчете потребное количество автомобилей равно
(3.70)
где t1—полное время одного цикла автосамосвала; t2—время погрузки самосвала.
Это выражение справедливо только при строгом соблюдении графика работы, цикличности подачи автомобиля, высокой надежности работы смесителя и самосвалов. Однако на практике такой синхронной работы не наблюдается. Время t1 цикла автосамосвала неодинаковое и изменяется на 100—200% в меньшую и большую сторону от среднего значения. Время погрузки также не одинаково.
Таким образом, рассматриваемая система не является конвейерной. Она функционирует как система массового обслуживания, поскольку поток требований и обслуживание этого потока базируется на случайных воздействиях. Следовательно, анализ системы может быть выполнен методами теории вероятностей.
Эта система с позиции теории вероятностей может находиться в различных условиях (вариантах): смеситель простаивает из-за отсутствия 1, 2, 3, ...,.N самосвалов; смеситель полностью загружен работой (максимальное обслуживание).
Вероятность каждого такого условия К вычисляют по формуле
(3.71)
88
З
десь N—количество автосамосвалов в обращении k = 0, 1, 2, 3, .... N; (м—среднее количество рейсов за 1 час работы, м ==1/t1;P0 —вероятность простоя смесителя; у— среднее количество самосвалов, находящихся под погрузкой в течение одного часа. Из этого уравнения вероятность простоя смесителя
3.72
Вероятность простоя каждого самосвала
(3.73)
Анализ показывает, что использование обычных методов расчета автомобилей (3.70) приводит к тому, что смеситель используют не полностью (максимум до 75%), а простои под погрузкой достигают 10%.
С увеличением процента использования смесителя резко возрастает потребность в автомобилях. Поэтому для выбора оптимального соотношения в системе «смеситель — автосамосвалы» необходимо продолжить исследование по экономическому критерию.
В системном анализе используются методы теории игр, которая рассматривает развитие процессов как случайные ситуации. Теория игр — это математическая теория конфликтов. Конфликт заключается в том, что интересы двух сторон не совпадают (борьба интересов) или стороны преследуют противоположные цели.
Примером конфликтной ситуации являются, например, все спортивные игры. Игрок выбирает такую совокупность правил поведения (стратегию), которая обеспечивает ему желаемый результат — выигрыш.
Как правило, теория игр рассматривает конфликтные ситуации, при которых приходится принимать решения с частичным или полным отсутствием данных об обстановке. Поэтому могут быть и случайные ходы, эффект которых можно оценить в среднем математическим ожиданием. Результат игры оценивают количественными показателями или условными числами: выигрыш + 1, ничья 0, проигрыш — 1.
Методы теории игр применяются не только для исследования в буквальном понятии конфликтных ситуаций, но и для решения задач, в которых, например, в качестве «противника» выступает природа. Такие задачи возникают при строительстве различных сооружений, организации работ, организации транспортных процессов в сельском хозяйстве, метеорологии и др.
С помощью теории игр можно оценить наиболее благоприятные и неблагоприятные ситуации и на основе полученных данных принять оптимальное для данных условий решение. В теории игр важное значение имеют понятия стратегии, под которым подразумевают правила поведения каждой стороны в ответ на действие другой стороны. Целью игры является обеспечение выигрыша.
89
Чаще применяют наиболее полно разработанную теорию парной игры с нулевой ничьей, когда исследуется задача с двумя противоположными сторонами А и В. При этом одна сторона выигрывает все что проигрывает другая, т.е. сумма выигрышей равна нулю
Если допустить, что каждая из сторон придерживается оптимальных стратегии, то они могут рассчитывать на равновесный средний выигрыш, называемый ценой игры у. Решить игру, значит найти пару оптимальных стратегий для А и В и цену игры. Игру называют конечной, если стороны располагают конечным числом стратегии Так. если А имеет т стратегий, а В-n, то игра называется m х п. Игровую стратегию задают матрицей игры (табл. 3.3).
Таблица 3.3
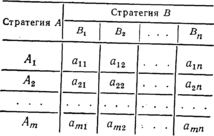
В матрице помещают средние выигрыши с соответствующей парой стратегий. Например, а12— это выигрыш стороны А со стратегией A1B2. При любой стратегии А сторона В стремится свести выигрыш А к минимуму aij. Поскольку имеет место множество стратегий, то сторона А находит такую стратегию, при которой максимальный выигрыш, т. е. определяются наиболее благоприятные условия игры для стороны А. Этот результат - максимальный выигрыш А при некотором противодействии B-а=mах х min аij (максимин) - называют нижней ценой игры. Такая стратегия всегда обеспечит стороне А выигрыш не ниже а. Аналогично для В существует минимальный проигрыш B==minmax aij. Величину В называют минимаксом или верхней ценой игры. Обычно ведут расчеты по принципу минимакса (принципу «осторожности»), т. е. находят такую стратегию, когда сторона А получает наилучший результат а при наихудших действиях стороны В. Этот принцип является основным в теории игр, он обеспечивает определенный запас в инженерных расчетах.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
