Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 5)

Тогда, согласно закону Гука при сдвиге и с учетом выражения

касательное напряжение равно

. (1)

Крутящий момент, действующий в данном сечении, равен

(2)

Отношение для данного сечения есть величина постоянная. Это погонный угол закручивания бруса, т. е. угол закручивания, приходящийся на единицу длины бруса. Эта величина не изменяется по площади сечения, поэтому этот член вынесен за знак интеграла. Модуль сдвига G – константа, его тоже вынесли за знак интеграла.

Обозначим - это полярный момент инерции, геометрическая характеристика сечения. Тогда из (2) получим и полный угол закручивания бруса будет равен

,

при = const и = const получим

где G - жесткость при кручении, которая зависит от материала бруса (G) и от формы сечения ( ).

Определение напряжений

По закону Гука .

Ранее получены выражения и , тогда

.

Касательные напряжения распределяются по сечению по линейному закону вдоль радиуса ρ (это расстояние от центра сечения до данной точки). Максимальные касательные напряжения возникают в точках сечения, наиболее удаленных от его центра (рис. 4.9а): . Если обозначить , получим

Здесь - момент сопротивления кручению, геометрическая характеристика сечения.

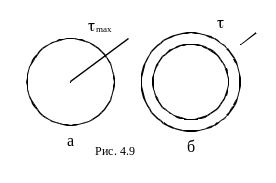
При кручении рациональным является кольцевое сечение, у которого вынут слабо напряженный материал вокруг центра, и распределение напряжений более близко к равномерному распределению (рис. 4.9б).

Л екция 5

Определение геометрических характеристик сечений

Сплошное круговое сечение, рис. 5.1

Элементарная площадь сечения равна

.

Толстостенная труба, рис. 5.2

Так как полярный момент инерции это интеграл, то для толстостенной трубы J_P можно определять как разницу между моментом инерции наружного контура и отверстия

_{Момент сопротивления кручению Wp - это не интеграл, а частное от деления Jp на rmax. Поэтому Wp нельзя определять как разницу между Wp наружного контура и внутреннего контура сечения.}

Тонкостенная труба (кольцевое сечение), рис. 5.3

Если отношение толщины стенки трубы к ее радиусу меньше 0,1 , то это тонкостенная труба и для такого сечения полярный момент инерции равен

,

Расчет на прочность при кручении

Поверочный расчет

Дано: материал, размеры конструкции, нагрузка.

Требуется определить коэффициент запаса.

Для пластичных материалов определяется коэффициент запаса по текучести .

Для хрупких материалов определяется коэффициент запаса по разрушению ,

где t_т - предел текучести при сдвиге и t_в - предел прочности при сдвиге заданы, а максимальное касательное напряжение t_max определяется из решения задачи.

Проектировочный расчет

Дано: материал, допустимое напряжение, нагрузка.

Требуется определить размеры сечения.

Или заданы размеры сечения и допустимое напряжение.

Требуется определить допустимую нагрузку.

Размеры сечения и допустимые нагрузки определяются из

условия прочности: t_max £ [t],

Допустимое напряжение [t] либо задано, либо определяется как отношение предельного напряжения к заданному коэффициенту запаса:

- для пластичных материалов, - для хрупких материалов.

Потенциальная энергия деформации и работа внешних сил

Рис.5.4 Рис 5.5

Момент М, закручивая валик, совершает работу на угле поворота торцевого сечения φ (рис. 5.4). Эта работа равна W= .

В формулах работы у нас всегда присутствует коэффициент , потому что силовой фактор работает на перемещении, которое сам же создает. Момент М постепенно возрастает от нуля до конечного значения и пропорционально ему растет угол φ (рис.5.5). Площадь треугольника на рис. 5.5 и есть работа, совершенная моментом М в процессе нагружения бруса.

При статическом нагружении в упругой зоне, если температура тела остается постоянной, потенциальная энергия деформации U равна работе внешних сил W. Крутящий момент М_к в данном случае равен М, тогда: .

_{Эта формула справедлива, если крутящий момент и жесткость валика постоянны}

_{(Mк=const и GJк=const). Если эти величины переменные, то потенциальную энергию надо определять с с помощью интеграла} .

Если валик имеет несколько участков, то потенциальная энергия суммируется по участкам

в этом выражении i - номер участка, n - число участков, M_кi - крутящий момент на i-том участке (берется с эпюры ), - жесткость i –того участка.

Если к брусу одновременно приложены несколько нагрузок (моментов), то для определения работы внешних сил надо просуммировать работу всех нагрузок:

,

Здесь j - номер внешнего момента (M_j это нагрузка, берем этот момент из условия задачи, т.е. с заданной схемы, не путать M_j с крутящим моментом ), m – число внешних моментов, j_j - угол поворота сечения, в котором приложен данный момент M_j. Значение j_j берем с эпюры углов закручивания валика. Если направление момента и угла закручивания сечения, в котором этот момент приложен, совпадают, то соответствующий член суммы будет с плюсом. В противном случае этот член будет с минусом.

Удельная потенциальная энергия деформации при сдвиге

У поверхности бруса, нагруженного моментами М, вырежем элементарный параллелепипед со сторонами dx, dy, dz, рис. 5.6. По его боковым граням действуют касательные напряжения t, а передняя и задняя грани элемента от напряжений свободны.

Рис. 5.6

Условно закрепим левый торец элемента. На рис. 5.6 показана деформация элемента в этом случае. По отношению к выделенному элементу действующие по его граням касательные напряжения являются внешними силами, совершающими работу на соответствующих перемещениях. При статическом нагружении в упругой зоне потенциальная энергия деформации равна работе внешних сил. Значит, потенциальная энергия деформации dU, накопленная в вырезанном элементе, равна работе dW, совершенной касательными напряжениями, действующими по правой грани этого элемента:

,

здесь t dx dy - элементарная сила, g dz - перемещение, dx dy dz = dV - элементарный объем. Поскольку, согласно закону Гука при сдвиге, то . Удельная потенциальная энергия деформации при сдвиге U₀ равна энергии dU, накопленной элементом, деленной на объем dV этого элемента:

, .

Кручение бруса прямоугольного поперечного сечения

При кручении брусьев некругового профиля их поперечные сечения не остаются плоскими, а сложным образом искривляются - «депланируют». На рис. 5.7 показан брус прямоугольного сечения после закручивания. Искажения ортогональной сетки, нанесенной на брус до нагружения, указывают на депланацию поперечных сечений, которые уже не остаются плоскими. Это обстоятельство настолько усложняет картину деформированного состояния таких брусьев, что решить подобную задачу методами сопротивления материалов не представляется возможным. Многие задачи этого класса решены методами теории упругости. При этом установлено, что

где W_к, J_к - геометрические характеристики, подобные W_p, J_p для бруса кругового сечения.

Распределение касательных напряжений по сечению и вдоль сторон контура показано на рис. 5.8. Точки, лежащие на оси бруса, и точки ребер призмы не напряжены (т. е. в угловых точках поперечного сечения касательные напряжения отсутствуют).

Наибольшие касательные напряжения возникают в точках поперечного сечения в середине длинных сторон прямоугольного контура сечения (точка D), в середине коротких сторон контура (точка E) напряжения несколько меньше.

Отсутствие касательных напряжений в углах контура доказывается с помощью свойства парности касательных напряжений. На рис. 5.9 изображена угловая точка C. Докажем отсутствие касательных напряжений в точке C методом от противного. Предположим, что в точке C есть касательное напряжение t_C. Разложим это напряжение на составляющие t_Cy и t_Cx, параллельные сторонам профиля. Тогда на основании закона парности касательных напряжений во взаимно перпендикулярных площадках (а это площадки, принадлежащие поверхности бруса) должны действовать такие же напряжения. Но поверхность бруса от напряжений свободна, значит, равны нулю составляющие t_Cy и t_Cx, а, следовательно, равно нулю и t_C - касательное напряжение в угловой точке C.

Из решения задачи методами теории упругости получены расчетные формулы для определения максимального касательного напряжения и угла закручивания бруса прямоугольного сечения:

, где _.

В этих формулах B < H, т. е. в квадрате и кубе стоит меньший размер.

Касательное напряжение в середине короткой стороны составляет долю от максимального касательного напряжения: t_E = h t_max (h < 1, для квадратного сечения h = 1).

Коэффициенты a, b, h зависят от - отношения сторон прямоугольного профиля.

Эти коэффициенты, найденные методами теории упругости, занесены в справочники. Некоторые значения этих коэффициентов приведены в таблице:

H /B	1	2	¥*)
a	0,208	0,246	0,333
b	0,141	0,229	0,333
h	1,0	0,795	0,742

^*) При можно считать, что

Лекция 6

Кручение бруса тонкостенного открытого профиля -

разомкнутое сечение

При расчете брусьев тонкостенного разомкнутого сечения профиль распрямляем (рис. 6.1) и используем формулы для расчета брусьев прямоугольного сечения.

, (1)

В выражении (1) и , где Н = S - длина средней линии исходного сечения, B = h - толщина сечения.

Характеристики

Список файлов ответов (шпаргалок)