Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 9)

2. Построить эпюры изгибающих моментов от внешних сил и от единичного фактора (т. е. эпюры М_x и М₁).

3. Эти эпюры по участкам перемножить, что означает, площадь одной эпюры умножается на ординату другой под центром тяжести первой.

Та эпюра, на которой берем ординату, в пределах участка должна быть линейной и не иметь излома.

Если эпюры расположены по разные стороны балки, то их произведение будет с минусом.

Результат расчета со знаком минусом означает, что перемещение будет в сторону, противоположную направлению приложенного единичного фактора.

4. Если эпюра М_x сложная, то ее можно «расслоить», т. е. разбить на такие фигуры, для которых известна величина площади и положение центра тяжести этой площади. Это, например, прямоугольник, треугольник и некоторые другие фигуры.

Площади элементарных фигур и положение их центра тяжести

На рисунках С – центр тяжести фигуры, А – площадь фигуры

Лекция 10

Косой изгиб

Если плоскость изгибающего момента не проходит через главную ось сечения, то такой вид нагружения называется косым изгибом. Главными называются оси, относительно которых центробежный момент инерции равен нулю ( ), а осевые моменты инерции имеют экстремальное значение, т. е. один из них это J_max, а другой J_min. Заметим, что ось симметрии всегда является главной осью, а вторая главная ось ей перпендикулярна и в наших задачах проходит через центр тяжести сечения.

Рассмотрим чистый косой изгиб. Определим положение нейтральной линии и максимальные напряжения при косом изгибе. В качестве примера рассмотрим брус, сечение которого изображенное на рис. 10.1.

В этом сечении действует изгибающий момент М. Ось симметрии y и перпендикулярная ей ось x - главные центральные оси сечения. Ось z проходит через центр тяжести сечения точку С. След моментной плоскости (моментная линия) не проходит через главные оси сечения, значит, это косой изгиб. Разложим изгибающий момент M по главным осям сечения. Получим изгибающие моменты, действующие относительно главных осей x, y. Это моменты M_x = M sin a и момент M_y = M cos a. Следует помнить, что изгибающий момент носит индекс той оси, вокруг которой он действует, так момент M_x действует в плоскости yz вокруг оси x, а момент M_y действует в плоскости xz вокруг оси y. Выберем систему координат как указано на рис. 10.1. Обозначим первую четверть. Запишем выражение для напряжения в произвольной точке A(x, y) этой четверти как сумму напряжений от моментов M_x и M_y :

(1)

При записи выражения (1) применен принцип независимости действия сил (метод суперпозиции, или наложения), когда напряжения (или перемещения) определяются от каждого фактора отдельно, а результаты складываются. Составляя выражение (1), напряжения растяжения записываем с плюсом, а напряжения сжатия - с минусом. В нашем случае оба напряжения – растяжение, поэтому они оба с плюсом. Определим положение нейтральной линии. Если точка лежит на нейтральной линии, то напряжение в ней равно нулю. Приравняв к нулю выражение (1), получаем уравнение нейтральной линии

Это уравнение можно привести к виду

. (2)

Выражение (2) - это уравнение прямой, проходящей через начало координат (в нашем случае через центр тяжести сечения) под углом b к оси x (рис. 10.2).

Рис. 10.2

Положительный угол b откладывается против часовой стрелки. В нашем примере согласно выражению (2) тангенс угла наклона нейтральной линии равен .

Преобразуем выражение для тангенса, подставив значения моментов M_x и M_y:

, отсюда . (3)

Если линии взаимно перпендикулярны, то произведение этих тангенсов должно равняться минус единице (tga tgb = -1). В общем случае моменты инерции не равны друг другу (J_x ¹ J_y), значит, tga tgb ¹ -1 и нейтральная линия, наклоненная к оси x под углом b, не перпендикулярна моментной линии, наклоненной к оси x под углом a.

В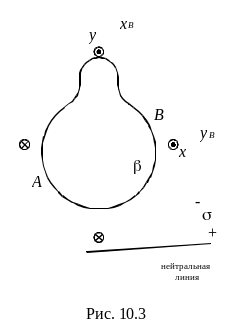 ывод: при косом изгибе нейтральная линия проходит через центр тяжести сечения, но она не перпендикулярна моментной линии. Можно доказать, что нейтральная линия отклоняется от перпендикулярного положения к оси минимум, т. е. к той оси, относительно которой момент инерции минимальный. Следовательно, балка гнется не в той плоскости, в которой ее изгибают (т. е. в плоскости действия изгибающего момента), а в некоторой другой плоскости, более близкой к плоскости минимальной жесткости. Отсюда и название «косой изгиб».

Определим максимальное напряжение при косом изгибе. Для этого сначала найдем опасную точку. Проведем нейтральную линию, которая отделяет растянутые слои от сжатых слоев. Согласно формуле (3) угол b в нашем случае отрицательный, отложим его по часовой стрелке. Нейтральная линия проходит через центр тяжести сечения под углом b к оси x, рис. 10.3. Следует обязательно проконтролировать, разделяет ли нейтральная линия растяжение и сжатие, т. е. отделяет «точки» от «крестиков». Если нет, то надо проверить предыдущие расчеты. Затем проводим линии, параллельные нейтральной линии и касательные к контуру сечения, рис. 10.3. Опасной будет точка, наиболее удаленная от нейтральной линии. В нашем случае очевидно это точка В, в которой складываются напряжения растяжения от моментов M_x и M_y . В точке А возникает напряжение сжатия. Предположим, что это напряжение получается равным по величине напряжению в точке В. Если в двух точках возникают равные по величине, но противоположные по знаку напряжения, то следует рассматривать ту точку, в которой действует напряжение растяжения, так как некоторые материалы работают на растяжение хуже, чем на сжатие. Когда из чертежа неясно, которое напряжение больше, надо рассмотреть обе точки, определить в них напряжения (в нашем случае это точки А и В) и выбрать ту, в которой напряжение больше. Построим эпюру нормальных напряжений в произвольном масштабе (рис. 10.3) и определим максимальное напряжение в точке В как сумму напряжений от каждого момента отдельно:

(4)

В выражении (4) - координаты точки В относительно главных центральных осей x, y. Поскольку, записывая выражение для напряжения, брали растяжение с плюсом, а сжатие с минусом (т.е. знаки уже учли), то координаты точки В следует брать по модулю, без учета знака относительно осей координат.

Внецентренное растяжение, сжатие

Если равнодействующая внешних сил не совпадает с осью сечения, но ей параллельна, то такой вид нагружения называется внецентренным растяжением, сжатием. Для решения задачи переносим все силы в центр тяжести сечения и добавляем изгибающие моменты относительно главных центральных осей. Получаем косой изгиб с растяжением или сжатием. Рассмотрим задачу на примере бруса, изображенного на рис. 10.4а. Для этого бруса требуется определить положение нейтральной линии и величину максимального напряжения.

Действующая на брус сила 2F параллельна оси бруса, но не проходит через центр

тяжести сечения. Переносим эту силу в центр тяжести сечения и добавляем изгибающие моменты относительно главных центральных осей x, y. Результат этого действия изображен на рис. 10.4б. Получили брус с действующими на него моментами и осевой силой, т.е. косой изгиб и растяжение. В общем случае надо сначала определить положение центра тяжести сечения и провести главные центральные оси, а затем переносить силы в центр тяжести сечения и добавлять соответствующие изгибающие моменты.

а б

Рис. 10.4

Подсчитаем геометрию сечения бруса, изображенного на рис.10.4:

.

Все сечения равноопасны. Изобразим одно из сечений (рис.10.5), приложив в нем внутренние суммарные силовые факторы - изгибающие моменты M_x = 2FB и M_y = FB, а также осевую растягивающую силу N = 2F.

Рис.10.5

Следует помнить, что момент носит индекс той оси, относительно которой он действует. Выберем первую четверть. Для произвольной точки этой четверти запишем выражение для напряжения как сумму напряжений от каждого из трех внутренних силовых факторов. Напряжения растяжения записываем с плюсом, а сжатия с минусом. В нашем примере и от изгибающих моментов, и от осевой силы в первой четверти будет растяжение, поэтому все члены с плюсом:

Характеристики

Список файлов ответов (шпаргалок)