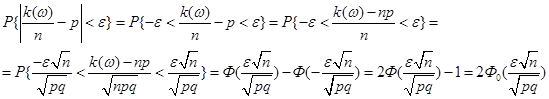Сформулируйте центральную предельную теорему. Сформулируйте и докажите теорему Муавра-Лапласа
Сформулируйте центральную предельную теорему. Сформулируйте и докажите теорему Муавра-Лапласа.
Центральная предельная теорема. Пусть X1, X2, …, Xn, … - последовательность независимых одинаково распределенных случайных величин, MXn=m, DXn=s2. Тогда 
, где Ф(x) – функция стандартного нормального распределения.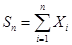 
Интегральная теорема Муавра-Лапласа. Обозначим Sn суммарное число успехов в n испытаниях по схеме Бернулли с вероятностью успеха p и вероятностью неудачи q=1-p. Тогда с ростом n последовательность функций распределения случайных величин 
сходится к функции стандартного нормального распределения, т. е. 
.
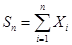
Доказательство. Пусть Xi – число успехов в i-м испытании. Тогда MXi=p, DXi=pq. Представляя Sn в виде Sn=X1+X2+…+Xn и используя центральную предельную теорему, приходим к утверждению теоремы.
34. Пусть 
– число успехов в серии из n испытаний по схеме Бернулли и n – велико.
Докажите, что в этом случае 
, где p – вероятность «успеха» в каждом отдельном испытании.
Д-во: 
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
