Литература и список обозначений
Литература.
1. А.Н.Ширяев. Вероятность. М.: Наука, 1980, 576с.
2. А.Д.Вентцель. Курс теории случайных процессов. М.: Наука, 1996, 399с.
3. Ж.Невё. Математические основания теории вероятностей. М.: Мир, 1969, 309с.
4. И.И.Гихман, Н.В.Скороход. Теория случайных процессов, т.2. М.: Наука, 1973, 639с.
5. Е.Б.Дынкин. Марковские процессы. М.: Физматиз, 1963, 859с.
6. Р.Ш.Липцер, А.Н.Ширяев. Статистика случайных процессов. М.: Наука, 1974, 696с.
7. Р.Ш.Липцер, А.Н.Ширяев. Теория мартингалов. М.: Наука, 1986, 512с.
8. Ж.Жакод, А.Н.Ширяев. Предельные теоремы для случайных процессов, т1. М.: Физ-мат. лит., 1994, 542с.
Рекомендуемые материалы
9. Р.А.Мейер. Вероятность и потенциалы. М.: Мир, 1973, 324с.
10. Дж.Дуб. Вероятностные процессы. М.: ИЛ, 1956, 605с.
11. П.Халмош. Теория меры М.: ИЛ, 1953, 291с.
12. П.Биллингсли. Сходимость вероятностных мер. М.: Наука, 1977, 351с.
13. А.Н. Колмогоров, С.В.Фомин. Элементы теории функций и функционального анализа. М.: Наука, 1989, 496с.
14. P.Bremand. Point Processes and Queunes (Martingale Dynamics). Springer-Verlag, New York-Heideberg-Berlin, 1981, 354p.
15. Н.Н.Лебедев. Специальные функции и их приложения. М.: Физ-мат. лит., 1963, 358с.
16. А.В.Булинский, А.Н.Ширяев. Теория случайных процессов. М.: Физ-мат. лит., 2003, 400с.
17. Б.Оксендаль. Стохастические дифференциальные уравнения. Введение в теорию и приложения. М.: Мир, 2003, 408с.
Список обозначений.
 - принадлежит
- принадлежит
 - пересечение
- пересечение
 - объединение
- объединение
 - дополнение
- дополнение
 - включение
- включение
 - пустое множество
- пустое множество
 - любой
- любой
 - существует
- существует
! - единственный
 - по определению
- по определению
 - градиент
- градиент
 - сумма
- сумма
 - произведение
- произведение
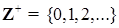
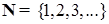
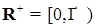
 - n-мерное евклидово пространство
- n-мерное евклидово пространство
 - польское (полное метрическое сепарабельное) пространство
- польское (полное метрическое сепарабельное) пространство
 - σ-алгебра борелевских множеств на
- σ-алгебра борелевских множеств на 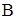
 - индикатор множества А
- индикатор множества А
 - декартово произведение множеств X и Y
- декартово произведение множеств X и Y
 - σ-алгебра, равная произведению σ-алгебр
- σ-алгебра, равная произведению σ-алгебр  и
и 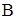
 - точная верхняя (нижняя) грань
- точная верхняя (нижняя) грань
 - предел
- предел
 - нижний (верхний) предел
- нижний (верхний) предел
В лекции "21. Электромагнитные исполнительные устройства" также много полезной информации.
 - монотонно стремиться снизу (сверху)
- монотонно стремиться снизу (сверху)
 - знак для различных видов сходимости
- знак для различных видов сходимости
 - отображение
- отображение 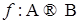
 - пространство непрерывных ограниченных функций на Е со значениями в
- пространство непрерывных ограниченных функций на Е со значениями в 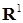
 - пространство измеримых ограниченных функций на Е со значениями в
- пространство измеримых ограниченных функций на Е со значениями в 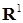
 - норма
- норма





















