Приложения теории точечных процессов. Элементы теории восстановления

Глава 4. Приложения теории точечных процессов.

Введение.

В этой главе мы рассматриваем два направления, в которых применяется теория точечных процессов, теория восстановления и теория массового обслуживания.

§1. Элементы теории восстановления.

1.1. Рассмотрим вероятностное пространство . Пусть на нём задана последовательность неотрицательных, независимых в совокупности, одинаково распределённых, случайных величин , с функцией распределения . Обозначим  и . Положим  - считающий процесс. Этот процесс в теории восстановления называют простым процессом восстановления, который имеет следующую интерпретацию: в момент времени нуль начинает функционировать некоторое устройство, которое функционирует до момента времени , в момент времени  оно выходит из строя, т.е. ломается, его мгновенно ремонтируют и снова это устройство нормально функционирует до момента времени , в момент времени  оно выходит из строя и его мгновенно ремонтируют и т. д. Очевидно, что N(t) - это число восстановлений устройства к моменту времени t.

1.2. Обозначим через  - функцию распределения случайной величины

, т.е. . Так как , то  равно n-кратной свёртке функции распределения , которую обозначим через . Ясно, что .

Рекомендуемые материалы

Обозначим через – среднее число восстановлений за время t, называемое функцией восстановления. Ясно, что . Возникает вопрос: как подсчитать вероятность ?

Теорема 1. .

Доказательство. Очевидно, что . Рассмотрим , очевидно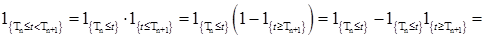 

.

Последнее равенство имеет место, так как . Возьмём теперь математическое ожидание относительно левой и правой частей получившегося равенства. В результате получаем утверждение теоремы.

Доказательство закончено.

1.3. Выведем теперь уравнение, которому удовлетворяет функция восстановления H(t).

Теорема 2. H(t) удовлетворяет уравнению

                                                          (1)

(Уравнение (1) называют уравнением восстановления).

Доказательство. Из определения функции восстановления H(t) и теоремы 1, имеем

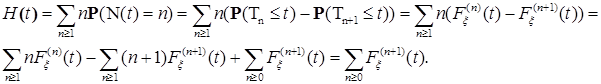
Так как , то . Поэтому ряд  - сходится. Отсюда следует: 

.

Поэтому в силу теоремы Фубини имеем:

.

Доказательство закончено.

1.4. Приведём теперь утверждение, касающееся разрешимости уравнения восстановления.

Теорема 3. Пусть . Тогда справедливы следующие утверждения.

1) Уравнение восстановления имеет единственное решение.

2) Если решение уравнения (1) существует и единственно, то оно допускает представление

                                                                     (2)

Доказательство. 1) Существование следует из сходимости ряда  для .

2) Второе утверждение устанавливается путём подстановки (2) в уравнение восстановления. Единственность очевидна. Доказательство закончено.

1.5. Определение. Пусть – последовательность независимых в совокупности положительных случайных величин, причём имеет функцию распределения , – одинаково распределённые случайные величины с функцией распределения F(t), причем . Обозначим . Точечный процесс  называется сложным процессом восстановления или процессом восстановления с запаздыванием, а  называется функцией восстановления сложного процесса восстановления.

Теорема 4.  удовлетворяет уравнению

                                    .                     (3)

Доказательство почти дословно повторяет доказательство теоремы 2.

1.6. Замечание. Решение уравнений (2) и (3) можно построить с помощью преобразования Лапласа-Стилтьеса. Напомним ,  () называются преобразованиями Лапласа - Стилтьеса соответственно, функций восстановления H(t)  и распределения  . Из этих определений следует, что  (). Поэтому  ().

Отметим также, если существует плотность , то существует обратное преобразование Лапласа. В этом случае легко установить, что существует , называемая плотностью функции восстановления, которая удовлетворяет уравнению

.

Если ,

то . Кроме того, .

1.7. Приведём теперь формулировки одного из центральных утверждений теории восстановления.

Теорема 5 (Элементарная теорема восстановления). Пусть . Пусть P – п.н.  при . Тогда  при .

Доказательство (набросок). Так как – точечный процесс, то  - п. н. . Разделим правую и левую части этого неравенства на , имеем - п. н.

Вам также может быть полезна лекция "3.5 Борьба русского народа за независимость".

 .

Очевидно - п. н. при . Поэтому  при  в силу закона больших чисел. Доказательство закончено.

1.8. Для формулировки ряда других утверждений напомним некоторые определения из теории вероятностей.

Определение. Точка а называется точкой роста функции распределения F(x), если из того, что "b>a, следует, что F(b)>F(a).

Определение. Распределение F(x) называется решетчатым, если существует число такое, что множество точек роста кратно . Если такого числа  не существует, то такое распределение называется неарифметическим.

Теорема 6. (Блекуэлла) Пусть – неарифметическая функция распределения. Тогда , где .