Приложение Е Системы уравнений
П.7. Системы уравнений
Система n линейных уравнений c неизвестными х1, х2,..., хp
а11х1+а12х2+...+а1pхp=с1
а21х1+а22х2+...+а2pхp=с2
... (П.7.1)
аn1х1+аn2х2+...+аnpхp=сn
может быть записана в матричном виде
Ах=c, (П.7.2)
где А=Аnр, х=хр1 и с=сn1. Заметим, что если n≠р, то х и с имеют различные размеры. Если n=р и матрица А невырожденная, то, в силу (П.5.3), система (П.7.2) имеет единственное решение в виде х=A–1c. Если n > р и матрица А имеет больше строк чем столбцов, то система уравнений Ax=с, как правило, не имеет решения. Если n < р и А имеет меньшее строк чем столбцов, то Ax=с, как правило, имеет бесконечное число решений.
Рекомендуемые материалы
Если система уравнений Ax=с имеет одно или более решений (значений вектора х), то она является совместной. Если система не имеет решения, то она называется несовместной [Беклемишев (2006) стр.147].
Чтобы показать структуру совместной системы уравнений Ax=с, предположим, что матрица А=Арр ранга r < р. Тогда строки матрицы А линейно зависимы и существует некоторый вектор b такой, что [см. (П.3.4)]
bTA=b1a1с+b2a2с+...+bpapс=0T.
Тогда должно быть и bTс=b1с1+b2с2+...+bpсp=0, так как умножение Ax=с слева на bT дает bTAx=bTс или 0Tx=bTс. В противном случае, если bTс≠0, то нет такого х, чтобы Ax=с. Следовательно, для того чтобы система уравнений Ax=с была совместной, те же линейные связи, если они существуют между строками матрицы А, должны существовать и между элементами вектора с. Это проверяется путем сравнения ранга матрицы А с рангом увеличенной матрицы [A, с]. Обозначение [A, с] указывает на то, что вектор с добавлен к матрице А в качестве дополнительного столбца.
Теорема П.7. Система уравнений Ax=с имеет по крайней мере одно решение (вектор х), если и только если ранг(А)=ранг[А, с].
Доказательство: Допустим, что ранг(А)=ранг[А, с], так что добавление вектора с не меняет ранг матрицы А. В этом случае вектор с является линейной комбинацией столбцов матрицы А. То есть существует такой вектор х, что
х1a1+х2a2+...+хpap=с.
В силу (П.3.3), это можно записать в виде Ax=с. Таким образом, вектор х является решением.
Наоборот, допустим существует такое решение в виде вектора х, что Ax=с. В общем, ранг(А) ≤ ранг[А, с] [Harville (2008) стр.42]. Но поскольку существует такой вектор х, что Ax=с, то имеем
ранг[А, с]=ранг[А, Aх]=ранг{A[I, х]} ≤ ранг(А) [по пункту 1 теоремы П.4].
Отсюда
ранг(А) ≤ ранг[А, с] ≤ ранг(А),
и следовательно ранг(А)=ранг[А, с].
□
Совместная система уравнений может быть решена с помощью обычных методов излагаемых в элементарных курсах алгебры путём исключения переменных, например, добавлением одного уравнения к другому или решением одного уравнения для одной переменной и подстановкой её в другое уравнение. В этом процессе одна или несколько переменных могут в конце быть произвольными постоянными, создавая, таким образом, бесконечное число решений. Метод решения с применением обобщённых обратных матриц приводится в разделе П.8.2. Некоторые системы уравнений и их решения даются в следующих примерах.
Пример П.7.1. Рассмотрим систему уравнений
х1+2х2=4
х1–х2=1
х1+х2=3
или в матричном виде
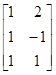
 =
= .
.
Расширенной матрицей этой системы является
[А, с]= ,
,
которая имеет ранг 2, так как третий столбец равен удвоенному первому плюс второму:
2 +
+ =
= .
.
Так как ранг(А)=ранг[А, с]=2, то система имеет по крайней мере одно решение. Если добавить два раза первое уравнение ко второму, то результат будет кратным третьему уравнению. Таким образом, третье уравнение является избыточным, а первые два легко могут быть решены для получения единственного решения хТ=[2, 1].
Три изображённые на рисунке П.7.1 линии представляют три уравнения. Обратим внимание, что эти линии пересекаются в точке (2, 1), которая является единственным решением трёх уравнений.
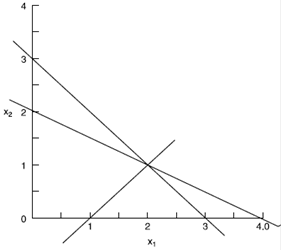
Рис. П.7.1. Три линии, представляющие три уравнения в примере П.7.1.
Пример П.7.2. Если изменить 3 на 2 в третьем уравнении примера П.7.1, то расширенная матрица становится
[А, с]= ,
,
которая имеет ранг 3, так как ни одна линейная комбинация её столбцов не равна 0. [В качестве альтернативы определитель det[А, с]≠0, и [А, с] невырожденная, см. пункт 3 теоремы П.9] Отсюда ранг[А, с]=3≠ранг(А)=2 и система получается несовместной.
На Рис. П.7.2 представляющие три уравнения линии показывают, что они не имеют общей точки пересечения. [Для получения "наилучшего" приближенного решения, один из способов его получения заключается в использовании метода наименьших квадратов, то есть нахождения таких значений x1 и x2, которые минимизируют сумму квадратов (х1+2х2–4)2+(х1–х2–1)2+(х1+х2–2)2.]
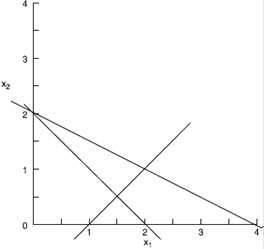
Рис. П.7.2 Три линии, представляющие три уравнения в примере П.7.2.
□
Пример П.7.3. Рассмотрим систему уравнений
х1+х2+х3=1
2х1+х2+3х3=5
3х1+2х2+4х3=6.
Третье уравнение представляет собой сумму первых двух, но второе не является кратным первого. Таким образом, ранг(А)=ранг[А, с]=2 и система совместная.
"Хорхе Луис Борхес" - тут тоже много полезного для Вас.
Решая первые два уравнения относительно x1 и x2 с использованием x3, получаем
х1=–2х3+4
х2=х3–3.
Вектор решения может быть представлен в виде
х= =х3
=х3 +
+ ,
,
где x3 - произвольная постоянная. Геометрически х является линией, представляющей пересечение двух плоскостей, соответствующих первым двум уравнениям.






















